Лекция 6. частотные свойства электрических

ЦЕПЕЙ СИНУСОИДАЛЬНОГО ТОКА

Известно, что алгебраическая форма комплексного сопротивления Z имеет действительную R и мнимую X части:

.

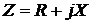Значения действительной и мнимой частей определяются составом и топологией схемы. Для схемы с последовательно включенными элементами R, L, и С реактивное сопротивление определяется выражением:

.

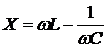Очевидно, что значение слагаемых реактивного сопротивления зависит от частоты ω. На малых частотах емкостная составляющая имеет большое значение, а индуктивная – малое. Поэтому реактивное сопротивление схемы Х принимает емкостной характер. На больших частотах Х принимает индуктивный характер.

Существует такая частота ω₀, на которой

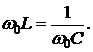
На этой частоте реактивное сопротивление равно нулю, а комплексное сопротивление цепи становится активным. Такой режим выделяют особо и называют резонансным. Под резонансным режимом работы электрической цепи понимают режим, при котором ее сопротивление является чисто активным.

Различают две разновидности резонансных режимов: резонанс токов и резонанс напряжений. Рассмотрим каждый из режимов.

1. РЕЗОНАНС ТОКОВ

Резонанс токов возникает в цепи с параллельным включением элементов (рис.6.1). Такая цепь содержит два сложных потенциальных узла, а все элементы находятся под одним и тем же напряжением.

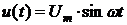. (6.1)

Для любого из узлов - 1 или 1’ справедлив первый закон Кирхгофа:

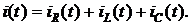(6.2)

Применяя к (6.2) выражения (1.7) и (1.12), приведем его к виду

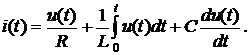(6.3)

Подставим в (6.3) вместо u(t) его значение из (6.1) и решим его:

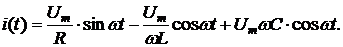(6.4)

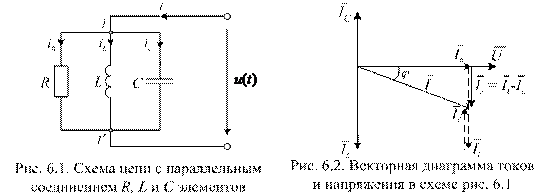
Векторная диаграмма, построенная по (6.4) приведена на рис. 6.2. В качестве исходного в ней принят общий для всех элементов цепи вектор напряжения 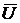. С этим вектором совпадает по направлению вектор тока через резистор. Его величина по модулю равна

.

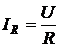Вектор тока через индуктивность – 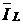отстает от вектора напряжения,

а вектор тока через емкость – 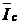опережает его на 90°.

Проведем последовательное сложение векторов 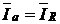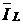и 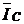. Результатом сложения является значение вектора тока – 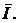Он сдвинут по фазе относительно вектора напряжения 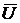на угол j. Сумма векторов 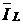и 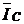дает значение вектора реактивного тока – 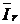. Модуль этого вектора определяется выражением:

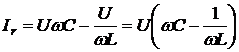. (6.5)

Векторы 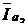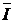и 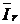образуют треугольник токов. Для этого треугольника справедливы выражения:

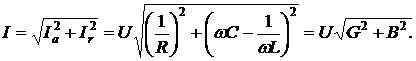(6.6)

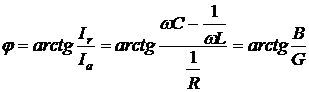. (6.7)

Треугольник токов наглядно показывает, что для достижения резонанса в цепи необходимо обеспечить равенства противофазных токов 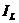и 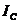. Тогда результирующий реактивный ток цепи 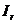и угол j будут равны нулю, а сопротивление цепи станет активным. Из выражения (6.5) следует, что ток 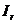может быть равен нулю при соблюдении условия

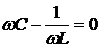. (6.8)

Выражение (6.8) позволяет определить

– резонансную частоту – ω₀, причем

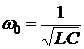; (6.9)

– значение одного из элементов L или С по заданному значению резонансной частоты – ω₀ и по известному значению другого элемента

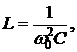
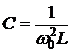. (6.10)

Определим значение тока всей цепи и токов, протекающих в ее ветвях в режиме резонанса. Действующее значение тока всей цепи 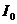на частоте 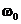легко найти по (6.6)

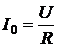. (6.11)

Но это значение равно току, протекающему через активное сопротивление цепи 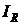, т.е.

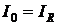. (6.12)

Ток, протекающий через элемент L, определим по закону Ома:

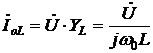. (6.13)

Подставляя в (6.13) вместо 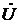его значение из (6.11), получим:

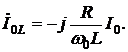(6.14)

Аналогично определим выражение для тока, протекающего через элемент С:

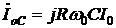. (6.15)

Сопоставим выражения (6.8), (6.14) и (6.15). Видим, что токи Ì_0C и Ì_0L равны по величине и противоположны по фазе (см. рис. 6.3). Величина Q_к равна

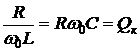, (6.16)

может быть больше единицы, в специальных устройствах достигает несколько десятков и сотен единиц и называется добротностью.

Еще раз подчеркнем замечательную особенность цепи в режиме резонанса. Токи, протекающие в ветвях реактивных элементов, могут принимать значения в десятки и сотни раз больше общего тока цепи. Поэтому резонанс цепи называют резонансом токов. Очень важно и то, что они противофазные. Именно это указывает на то, что в цепи происходит колебательный процесс с частотой 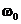по передаче электрической энергии конденсатора в магнитную энергию индуктивности и наоборот.

При идеальных элементах L и С энергия источника на этот процесс не затрачивается. Она расходуется только на преодоление сопротивления резистора R. Поэтому цепь рис.6.1. называют параллельным колебательным контуром.

Чтобы завершить анализ цепи, рассмотрим зависимость токов ее ветвей и напряжения между узлами U от частоты (рис.6.4). Ток, протекающий через элемент R - i_R, определяется законом Ома и не зависит от частоты. Ток через емкость i_c согласно (6.15) прямо пропорционален частоте, а ток через индуктивность i_L –обратно пропорционален. На частоте ω₀ они равны по величине, но противоположны по направлению. Общий ток цепи определяется суммой трех токов. Он имеет большое значение на частотах, значение которых значительно больше или меньше значения резонансной частоты.

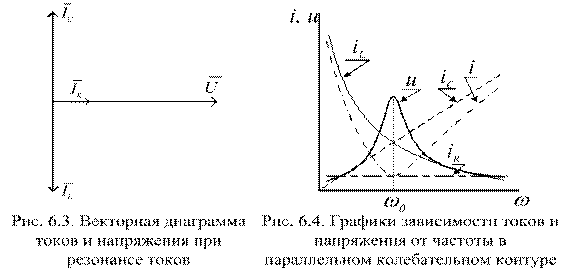
На резонансной частоте общий ток принимает значение i_R. Физически это означает, что на резонансной частоте проводимость цепи минимальна (она равна проводимости только элемента R). Поэтому падение напряжения между узлами цепи максимально на частоте ω₀ и уменьшается при удалении от ω₀. В силу этих качеств параллельный колебательный контур широко применяют в радио и радиотехнических устройствах для выделения сигналов на заданной частоте.

3. РЕЗОНАНС НАПРЯЖЕНИЙ

Резонанс напряжений возникает в цепи с последовательным соединением элементов (рис. 6.5). Известно, что комплексное сопротивление такой цепи определяется выражением

.

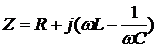По определению резонанс в цепи рис.6.5 наступает, когда выполнится условие

.

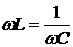Отсюда видно, что резонанс в цепи возникает на частоте

.

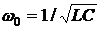Очевидно также, что

, .

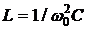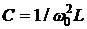Видим, что полученные выражения полностью соответствуют (6.9) и (6.10). Это подтверждает единство физической сути различных видов резонанса.

Определим ток и напряжение всей цепи, а также падение напряжения на ее отдельных элементах в режиме резонанса. Так как сопротивление всей цепи в режиме резонанса минимально и равно R, то ток в ней максимален и равен

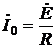. (6.17)

Падение напряжения на отдельных элементах легко найти по закону Ома. Так, падение напряжения на резисторе R равно

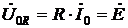. (6.18)

Тривиальный математически результат интересен по физической сути – при резонансе все напряжение источника выделяется на R элементе цепи.

Падение напряжения на индуктивности определяется выражением:

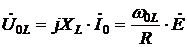. (6.19)

Величина

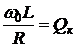(6.20)

называется добротностью и может принимать значение десятков и сотен единиц. Значит, падение напряжения на индуктивности может в десятки и сотни раз превышать Э.Д.С. источника.

Падение напряжения на емкости равно

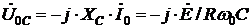. (6.21)

Так как 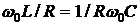, то падение напряжения на емкости равно по величине падению напряжения на индуктивности, но они противоположны по знаку. Отношение напряжения на индуктивности или на емкости в режиме резонанса к току в этом режиме называют характеристическим сопротивлением – ρ, причем

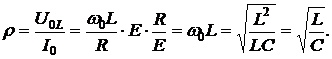(6.22)

В силу того, что

,

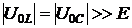рассматриваемый режим назван резонансом напряжений. Противоположность фаз напряжени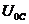й и 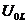указывает на то, что в цепи происходит такой же колебательный процесс с частотой ω₀, как и в параллельном колебательном контуре. Здесь также энергия источника затрачивается только на преодоление сопротивления резистора R. Поэтому цепь называется последовательным колебательным контуром.

Завершим анализ резонанса напряжений построением частотной зависимости тока цепи (рис.6.5) и падений напряжений на элементах L и С (рис.6.6).

На рисунке штрихпунктирной линией отмечен график ЭДС. На частоте ω=0 сопротивление идеальной индуктивности отсутствует. Поэтому падение напряжения u_L также равно нулю. С увеличением частоты сопротивление индуктивности, а значит, и падение напряжения на ней, увеличиваются. Когда частота устремляется в бесконечность, сопротивление Х_L также устремляется в бесконечность. При этом падение напряжения u_L стремится к Е. Между крайними точками графика u_L=ƒ(ω) существует экстремум напряжения 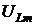, который находится по формуле

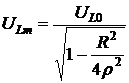. (6.23)

Частота, на которой достигается этот максимум, определяется формулой:

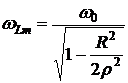. (6.24)

Сопротивление емкости на частоте ω=0 равно бесконечности. Значит,

напряжение на ее обкладках равно Е. С увеличением частоты сопротивление Х_С уменьшается. Когда частота устремляется в бесконечность, сопротивление X_C устремляется к нулю. Между крайними точками также существует экстремум, причем

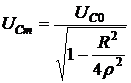. (6.25)

Частота, на которой достигается этот максимум, определяется выражением

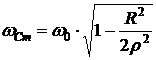. (6.26)

Так как подкоренное выражение в (6.24) и (6.26) всегда меньше единицы, то очевидно, что

.

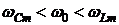Кроме того

.

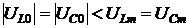В силу этих особенностей достоверным признаком наступления резонанса в цепи является максимум тока, значение которого изменяется с изменением частоты по резонансной кривой.

КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ

6.1. Объясните, чем определяется характер сопротивления электрической цепи синусоидального тока и как его можно изменять.

6.2. Сформулируйте определение резонанса цепи. Назовите виды резонанса, приведите их отличительные признаки и общие свойства.

6.3. Приведите выражения для добротности параллельного и последовательного колебательных контуров. Чем отличаются эти выражения?

6.4. В схеме рис. 6.1 известно: е(t) = 14,1 sin 314 t, R = 200 Ом, а L = 0,1 Гн. Определите значение емкости, при котором в цепи возникнет резонанс.

6.5. По данным задачи 6.4 определите добротность цепи рис. 6.1, общий ток цепи, а также токи ее ветвей.

6.6. Используя данные задачи 6.5, определите полную, активную и реактивную мощность цепи по схеме рис. 6.1. Сформулируйте предложение по способу увеличения коэффициента мощности цепей синусоидального тока.

6.7. Сформулируйте определение характеристического сопротивления.

6.8. В схеме рис. 6.5 известно: е(t) = 14,1 sin 314 t, R = 4,9 Ом, а L = 0,1 Гн. Определите значение емкости, при котором в цепи возникнет резонанс.

6.9. По данным задачи 6.8 определите добротность цепи рис. 6.5, общий ток цепи, а также падение напряжения на R, L и С элементах. Сравните полученные результаты с результатами задачи 6.5. Назовите параметры цепей, имеющие одинаковые и различные значения.