Лекция 2. методы анализа линейных электрических цепей постоянного тока

Реальные электротехнические устройства и системы имеют сложные схемы. Перед специалистами стоят задачи расчета их параметров. Процесс расчета параметров в теории электротехники принято называть «анализом схем». Электрические схемы любой сложности подчиняются законам Ома и Кирхгофа. Однако применение только этих законов часто приводит к неоправданно сложным решениям. Поэтому был разработан ряд методов анализа, адаптированных к топологии электрических цепей и упрощающих процесс расчета их параметров. В лекции рассматриваются некоторые из таких методов.

1. АНАЛИЗ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПРИМЕНЕНИЕМ ЗАКОНОВ КИРХГОФА

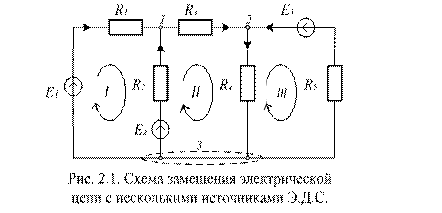
При анализе электрических цепей определяют значение токов в их ветвях, падение напряжения на элементах или потребляемую мощность по заданному значению Э.Д.С., а также значение сопротивлений, проводимостей или других параметров по заданным значениям тока или напряжения. Для определенности будем полагать, что расчету подлежит значение токов ветвей схемы, приведенной на рис. 2.1.

Суть анализа электрических цепей применением законов Кирхгофа

заключается в составлении системы из N независимых линейных уравнений,

причем

N = (n - 1) + к,

где: n – число сложных потенциальных узлов, к – число независимых контуров.

По первому закону Кирхгофа составляется (n - 1) уравнение, по второму закону – к уравнений.

Схема рис. 2.1 содержит 5 ветвей (N=5), 3 cложных потенциальных узла (n = 3) и 3 независимых контура (к=3). Значит, в систему необходимо включить два уравнения по первому закону Кирхгофа (например, для узлов 1 и 2) и три уравнения по второму закону Кирхгофа (для контуров I, II, III).

Обозначим на схеме стрелками условно принятые положительные направления токов ветвей и направления обхода контуров. Будем полагать, что индексы токов ветвей совпадают с индексами пассивных приемников электрической энергии. Тогда система уравнений по законам Кирхгофа принимает вид:

.

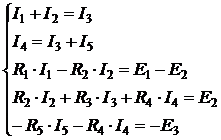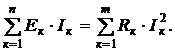Далее необходимо решить систему из пяти уравнений относительно токов. Точность расчетов может быть проверена с помощью уравнения баланса мощностей источников и приемников электрической энергии:

В левой части уравнения слагаемые имеют знак плюс, если направления Э.Д.С. и токов совпадают. В противном случае они имеют знак минус.

2. АНАЛИЗ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ МЕТОДОМ

ЭКВИВАЛЕНТНЫХ ПРЕОБРАЗОВАНИЙ

Когда в состав электрической цепи входит только один источник Э.Д.С., его ток определяется общим сопротивлением пассивных приемников электрической энергии. Такое сопротивление называют эквивалентным – Rэкв. Очевидно, что если известно Rэкв, то цепь можно представить в виде двух последовательно соединенных элементов – источника Э.Д.С. и Rэкв, а определение тока источника сводится к применению закона Ома. Процесс перехода от электрической цепи с произвольной топологией к цепи с Rэкв называется эквивалентным преобразованием. Такое преобразование и положено в основу рассматриваемого метода анализа.

Приемы преобразования электрической цепи определяются способами соединения пассивных элементов. Различают четыре основных способа соединения: последовательное, параллельное, треугольником и звездой. Рассмотрим сущность эквивалентных преобразований при каждом из названных способов.

2.1. Последовательное соединение элементов.

Электрическая схема с последовательным соединением элементов приведена на рис. 2.2, а. Такая цепь имеет только один контур. Через все элементы контура протекает один и тот же ток I. Согласно второму закону Кирхгофа, можно записать

R1 × I + R2 × I +¼+ Rn × I = Rэкв × I,

откуда

Rэкв = R1 + R2 +¼+ Rn, (2.1)

а

I = U / Rэкв.

Таким образом, видим, что схема из n последовательно соединенных резистивных элементов может быть заменена схемой с одним элементом, сопротивление которого определяется по (2.1).

2.2. Параллельное соединение элементов.

Параллельным называют соединение, при котором все элементы цепи присоединяются к двум сложным потенциальным узлам и находятся под воздействием одного и того же напряжения. Схема такой цепи приведена на рис. 2.3. Ток каждой к – ой ветви этой цепи определяется напряжением источника U и проводимостью G_к соответствующей ветви:

Iк = Gк × U. (2.2)

Определим правило эквивалентной замены разветвленной схемы рис.2.3, а на простейшую схему рис 2.3, б. Условием эквивалентности схем

является равенство токов на зажимах 1 – 1′, т. е.:

I = I₁ + I₂ + ∙∙∙ + I_n. (2.3)

Подставляя в (2.3) значение токов из (2.2), получим:

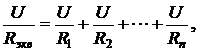(2.4)

откуда

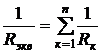
или в единицах проводимости

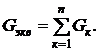(2.5)

Таким образом, цепь, состоящая из n параллельных резистивных элементов, может быть заменена простейшей цепью, эквивалентное сопротивление которой определяется выражением (2.5).

При параллельном соединении двух резистивных элементов с сопротивлениями R₁ и R₂ их эквивалентное сопротивление равно:

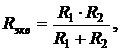(2.6)

а эквивалентная проводимость

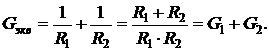(2.7)

Токи двух ветвей при их параллельном соединении определяются по правилу деления токов:

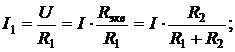
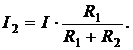(2.8)

2.3. Соединение элементов звездой или треугольником.

Соединение трех сопротивлений в виде трехлучевой звезды (рис. 2.4, а),

называют соединением «звезда», а соединение, при котором элементы образуют стороны треугольника (рис. 2.4, б), – «треугольник».

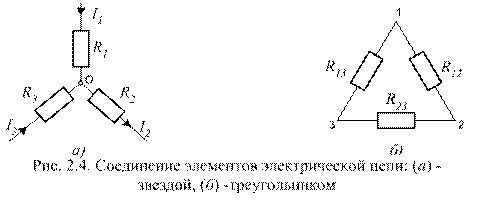Очень часто при расчете электрических цепей оказывается целесообразным преобразовать треугольник в звезду. Полезность преобразования наглядно видна на примере схемы рис. 2.5. На рис. 2.5, а приведена схема до преобразования. Пунктиром обведен преобразуемый треугольник. На рис. 2.5, б приведена та же схема после преобразования. Расчет токов в ней значительно проще.

При преобразовании треугольника в звезду следует пользоваться выражениями:

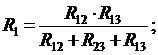
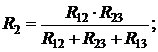
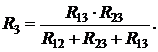`(2.9)

2.4. Метод эквивалентных преобразований.

Суть метода:

1.Участки электрической цепи с последовательно и параллельно

соединенными элементами заменяют одним эквивалентным элементом. Рядом последовательно выполненных преобразований схему упрощают до элементарного вида.

2.Применением закона Ома находится ток упрощенной схемы. Его значение определяет ток ветви, ближайшей к источнику Э.Д.С. (ток первой ветви). Это позволяет легко вычислить токи остальных ветвей.

Рассмотрим возможность применения метода на примере анализа схемы рис. 2.6, а. Будем полагать, что в схеме известны значение Э.Д.С. – Е и значения сопротивлений всех ветвей. Необходимо определить токи всех ветвей цепи.

Решение:

А) Выполняем ряд эквивалентных преобразований.

Для этого:

1) Выделяем участок с параллельно соединенными сопротивлениями R₄ и R_5. Находим эквивалентное сопротивление этого участка:

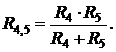
Приводим схему рис. 2.6, а к схеме рис. 2.6, б.

2) Находим эквивалентное сопротивление цепи относительно узлов а и б:

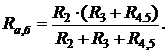
Теперь схема представляет контур с последовательно соединенными Е, R₁ и R_{а, б} элементами (рис. 2.6, в), т. е. приведена к простейшему виду.

Б) Определяем токи ветвей.

Для этого:

1) Находим ток простейшей схемы (ток первой ветви – I₁):

I₁ = Е / (R₁ + R_а,б).

2) Возвращаемся к схеме рис. 2.6, б. Учитывая, что теперь в схеме известен ток I₁, находим токи ветвей R₂ и R_3..Для этого достаточно применить правило деления токов (2.8):

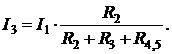
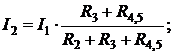
Очевидно, что после определения тока I₂, ток I₃ легко вычислить и по первому закону Кирхгофа, т. е. I₃ = I₁ – I₂.

3) Возвращаемся к схеме рис. 2.6, а. Так как теперь в схеме известны

токи I₁,I₂ и I₃, токи I₄ и I₅ находим по (2.8):

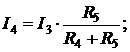
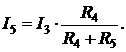
Таким образом, анализ электрической цепи рис. 2.6 проведен без составления и решения системы из N = 5 линейных уравнений по законам Кирхгофа. В этом и заключается его основное достоинство.

3. АНАЛИЗ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ МЕТОДОМ

КОНТУРНЫХ ТОКОВ

Метод контурных токов оказывается полезным, когда схема электри-

ческой цепи содержит несколько источников электрической энергии. Он позволяет выполнить анализ такой цепи решением системы из К канонических

уравнений, где К равно числу независимых контуров.

Напомним, что канонические уравнения удобны для матричной формы представления системы. В электротехнике матрицы применяют для сокращенной записи системы уравнений и для упорядочения их решения.

Члены канонических уравнений снабжаются двумя индексами, причем первый индекс соответствует номеру строки, а второй – номеру столбца. Если ввести понятия контурных токов, контурных сопротивлений и Э.Д.С., а также взаимных сопротивлений, то формально записанное каноническое уравнение соответствует уравнению, составленному по второму закону Кирхгофа.

Рассмотрим метод на примере схемы, приведенной на рис. 2.7, а. Схема имеет два независимых контура. Для ее анализа методом контурных то-

ков необходимо составить систему из двух канонических уравнений:

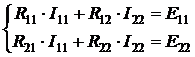, (2.10)

где: I₁₁, I₂₂ – контурные токи, Е₁₁, Е₂₂ – контурные Э.Д.С., R11, R22 – контурные сопротивления, R₁₂, R₂₁ – взаимные сопротивления контуров.

Определим введенные понятия.

Под контурными токами понимают условные (расчетные) токи, замыкающиеся в соответствующих контурах. На рис 2.7, а направление контурных токов показано стрелками в контурах. Пусть направление этих токов будет одинаковым – по часовой стрелке.

Сопоставляя контурные токи с токами ветвей, можно показать, что

значение контурных токов совпадает со значением действительных токов

только во внешних ветвях:

I₁₁ = I₁, I₂₂ = I₄.

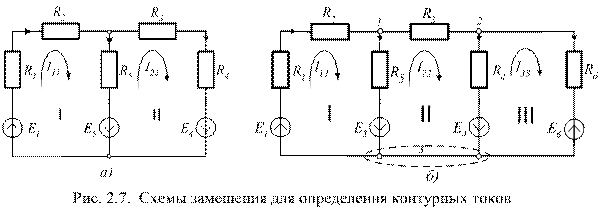
Токи смежных ветвей равны разности контурных токов соседних контуров:

I₅ = I₁₁ – I₂₂.

Таким образом, по известным контурным токам легко найти действительные токи всех ветвей. Следовательно, решение системы уравнений (2.10) относительно контурных токов отвечает целям анализа электрической цепи.

Для решения системы уравнений (2.10) определим понятия контурных сопротивлений – R₁₁, R₂₂, контурных Э.Д.С. – Е₁₁, Е₂₂ и взаимных сопротивлений – R₁₂, R₂₁:

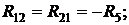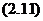R₁₁ = R₁ + R₂ + R₅, R₂₂ = R₃ + R₄ +R₅;

Е₁₁ = Е₁ + Е₅, Е₂₂ = Е₄ −Е₅.

Теперь уравнения системы (2.10) полностью соответствуют параметрам схемы рис. 2.7, а. Значение взаимных сопротивлений контуров в (2.11) определено с обратным знаком. Это обусловлено необходимостью привести канонические уравнения (2.10) в соответствие с уравнениями, составленными по второму закону Кирхгофа. Взаимное сопротивление контуров, не имеющих общих ветвей, равно нулю. Решая эту систему уравнений, можно найти контурные токи, а по ним искомые токи ветвей: I₁, I₂, I₃, I₄, I₅.

Если бы схема содержала три контура, как на рис. 2.7, б, то система канонических уравнений имела бы вид:

.

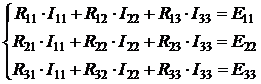Таким образом, метод контурных токов более экономен по вычислительной работе. Он позволяет формализовать процесс анализа и упрощает применение ЭВМ к анализу сложных электрических цепей.

4. АНАЛИЗ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ МЕТОДОМ

МЕЖДУУЗЛОВОГО НАПРЯЖЕНИЯ

В реальных электрических цепях часто источники и приемники электрической энергии включаются параллельно. Схемы таких цепей имеют только два узла. Если напряжение между узлами известно, то определение токов в ветвях цепи сводится к применению закона Ома. Этот факт и положен в основу метода. На первом этапе определяют междуузловое напряжение, а затем, применяя закон Ома, вычисляют токи ветвей.

Пусть анализу подлежит схема рис. 2.8, а. Схема содержит активные и пассивные ветви, соединенные параллельно. Определим токи всех ветвей цепи, применив метод междуузлового напряжения.

Формулу для междуузлового напряжения можно получить, используя принцип суперпозиции. Следуя этому принципу, сначала определим напряжение, создаваемое между узлами одним источником тока и одним источником Э.Д.С. Полученные выражения распространим на общий случай, когда в цепи действует m источников Э.Д.С. и к источников тока.

Обозначим сложные потенциальные узлы схемы индексами А и В. Напряжение U^I_АВ между узлами А и В, создаваемое только источником тока I, определим по схеме рис. 2.8, б. Согласно первому закону Кирхгофа, ток источника I равен сумме токов всех ветвей:

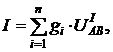(2.12)

где:g_i – проводимость i-ой ветви (кроме ветви с источником тока).

Отсюда

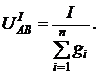(2.13)

Напряжение 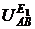между узлами А и В, создаваемое только источником Э.Д.С. Е_1, найдем по схеме рис.2.8, в. Заменим в схеме рис.2.8, в источник Э.Д.С. Е₁ эквивалентным источником тока. Схема примет вид рис.2.8, г. Теперь напряжение 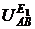, создаваемое источником Э.Д.С. Е_1, можно определить по (2.13):

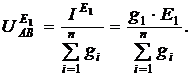(2.14)

Напряжение 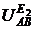от действия источника Э.Д.С. Е₂ найдем аналогично (2.14):

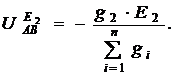(2.15)

Результирующее напряжение U_АВ, определим как сумму от воздейст-вия источников I, Е₁ и Е₂. Значения знаменателей в выражениях (2.13), (2.14), (2.15) одинаковы. Поэтому

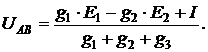
Если схема содержит к источников тока и m источников Э.Д.С., то напряжение U_АВ между узлами равно алгебраической сумме напряжений, создаваемых источниками тока и источниками Э.Д.С., т. е.

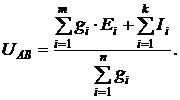(2.16)

В выражении (2.16) произведения g_i,∙E_i и I_i берут со знаком плюс, когда направления Е_i и I_i противоположны выбранному условно – положи тельному направлению напряжения U_АВ, и со знаком минус, когда эти

направления совпадают.

Зная междуузловое напряжение U_АВ, легко найти токи, как в пассивных, так и в активных ветвях цепи рис. 2.8, а:

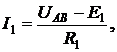
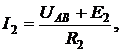
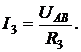
5. АНАЛИЗ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ МЕТОДОМ АКТИВНОГО

ЭКВИВАЛЕНТНОГО ДВУХПОЛЮСНИКА

При анализе сложных электрических цепей часто интересуются элек-трическим состоянием лишь одной ветви. В таком случае полезен метод эк-вивалентного генератора (метод активного эквивалентного двухполюсника). Обоснованием данного метода является теорема об активном эквивалентном двухполюснике. Теорема утверждает, что любую, сколь угодно сложную электрическую цепь или ее часть, можно представить активным эквивалентным двухполюсником с параметрами Е_экв и R_экв. Режим работы ветви, присоединенной к двухполюснику, при этом не изменится.

Пусть анализу подлежит схема электрической цепи, приведенной на рис. 2.9, а. Предположим, что в этой цепи нас интересуют напряжение и ток только одной ветви – R₃. Решим задачу применением метода активного эквивалентного двухполюсника. Для этого всю схему, кроме ветви R₃, представим активным двухполюсником (рис. 2.9, б). К зажимам двухполюсника а и б присоединим ветвь R₃.

Параметры двухполюсника R_экв и Е_экв определяются составом и топологией схемы цепи рис. 2.9, а. Поэтому режим работы ветви R₃ не изменился. Но теперь для определения тока в ней достаточно применить закон Ома:

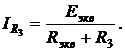(2.17)

В этом и заключается преимущество рассматриваемого метода.

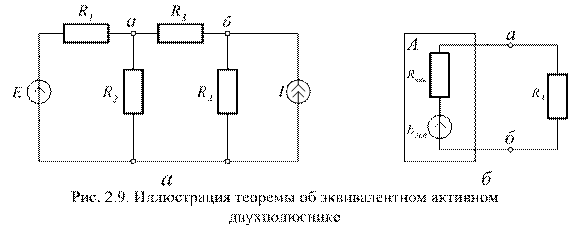
Для решения (2.17) необходимо определить значения Е_экв и R_экв. Значение Е_экв определяют исходя из того, что напряжение U_хх на разомкнутых зажимах источника равно значению его Э.Д.С. – Е_экв.

Разомкнем зажимы а, б. Схема рис. 2.9, а примет вид рис. 2.10, а. Напряжение между разомкнутыми узлами а, б – U_хх = Е_экв. Схема рис. 2.10, а позволяет определить это напряжение, используя принцип суперпозиции. Для этого последовательно определяем напряжение узла а, затем узла б, а затем вычисляем разность напряжений.

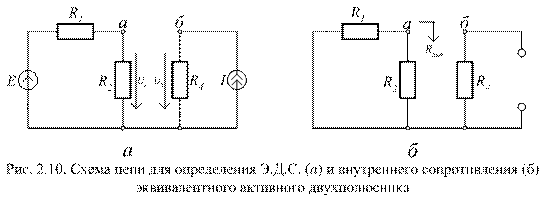
Напряжение узла а:

U_а = I₁ ∙ R₂ = E ∙ R₂/(R₁ + R₂).

Напряжение узла б:

U_б = I ∙ R₄.

Тогда

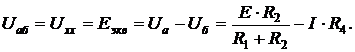
Эквивалентное сопротивление активного двухполюсника – R_экв находится также относительно разомкнутых зажимов а, б. Однако дополнительно требуется исключить источники электрической энергии. Правила

исключения источников заключаются в следующем.

При исключении источника Э.Д.С. полагают, что напряжение на его зажимах и внутреннее сопротивление равны нулю. Поэтому зажимы источника Э.Д.С. замыкают накоротко.

При исключении источника тока полагают, что ток источника равен нулю, а внутреннее сопротивление – бесконечности. Поэтому зажимы источника тока разрываются.

После исключения источников электрической энергии схема рис. 2.10, а приходит к виду рис. 2.10, б (полагаем, что между узлами а, б сохраняется режим холостого хода). Теперь очевидно, что эквивалентное сопротивление активного двухполюсника – R_экв определится выражением:

.

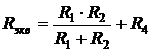Подставляя выражения, полученные для Е_экв и R_экв в (2.17), получим:

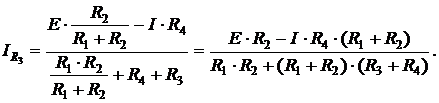
Таким образом, метод активного эквивалентного двухполюсника существенно упрощает процесс анализа, но требует определенных навыков в преобразовании топологии схемы к удобному и наглядному виду.

7. КЛАССИЧЕСКИЙ МЕТОД АНАЛИЗА

ПЕРЕХОДНЫХ ПРОЦЕССОВ

К анализу переходных процессов применяют классический, операторный методы или метод с использованием интеграла Дюамеля. Рассмотрим классический метод анализа переходного процесса.

2.1. Заряд и разряд ёмкости через резистор

Пусть задана цепь, приведённая на рис. 2.11.

Для такой цепи справедливо равенство

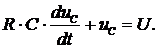(2.18)

Полученное выражение представляет собой дифференциальное уравнение. Интеграл от такого уравнения представляет сумму частного решения данного неоднородного уравнения и общего решения однородного уравнения. Токи и напряжения, полученные в результате частного решения, называют установившимися или принуждёнными i_у, u_у, i_пр, u_пр.

Однородное уравнение получаем при равенстве нулю правой части (2.18). Токи и напряжения, полученные в результате общего решения, определяются лишь параметрами элементов цепи и называются свободными i_св, u_св.

Сумма установившихся и свободных токов и напряжений определяют переходные токи и напряжения:

u_пер = u_у +u_св.

Частное решение находят для установившегося режима, когда переходный процесс закончен. Для рассматриваемой цепи при t→∞

u_су = U.

Выражение для свободного напряжения u_св определяется решением однородного дифференциального уравнения

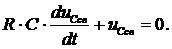
Преобразуем его к виду:

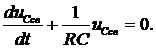
Решением этого уравнения является функция 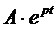. Здесь А – постоянный коэффициент, р – корень характеристического уравнения

.

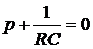Нетрудно видеть, что корень этого уравнения .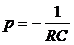

Таким образом

.

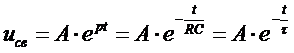Видим, что свободная составляющая напряжения на емкости в момент коммутации скачком принимает значение А. Величину τ = RC называют постоянной времени. Она имеет размерность времени и характеризует длительность переходного процесса, т. е. время, в течение которого u_Ссв уменьшается в е раз по сравнению с начальным значением u_Ссв (0) = А.

С учётом полученных выражений можем записать

.

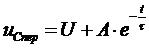Для определения А воспользуемся вторым законом коммутации. В момент, предшествующий коммутации, конденсатор С был разряжен. Следовательно, и в первый момент после коммутации напряжение на емкости останется без изменения. Значит, можем записать

U_C(0₊) = U + A = 0

и

А = -U.

Теперь очевидно, что

,

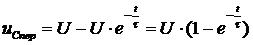Ток в цепи во время переходного процесса

,

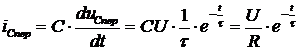т. е., ток в цепи с емкостью изменяется скачком до значения .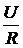

Графики напряжения и тока анализируемой цепи приведены на рис. 2.12.

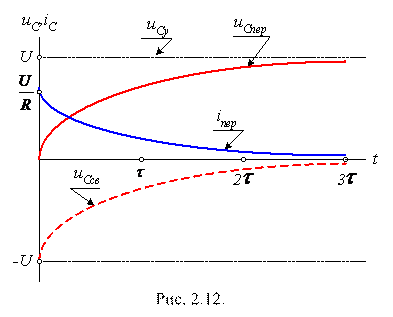
Переходный ток цепи с ёмкостью может изменяться скачком. Если активное сопротивление цепи мало, то ток в момент включения источника напряжения может быть значительно больше номинального значения.

При разряде конденсатора ёмкостью С, заряженного до напряжения U₀,на резистор R необходимо учитывать, что источник в цепи отсутствует и 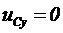(см. рис 2.13). Напряжение .

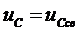Согласно второму закону Кирхгофа

u_Ссв - R·i = 0.

или

.

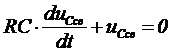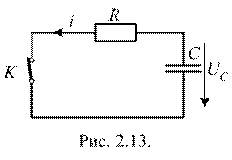
Это однородное дифференциальное уравнение. Его решение имеет вид

.

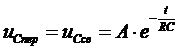В момент t = 0 u_Ссв = U₀, поэтому А = U₀. Следовательно

.

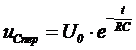Переходной ток определяется выражением

.

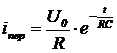Длительность переходного процесса при разряде, так же как и при заряде ёмкости, определяется постоянной времени τ.

2.2. Подключение индуктивности к источнику

постоянного напряжения

Пусть задана цепь, приведённая на рис. 2.14.

Для такой цепи справедливо выражение

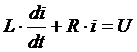. (2.19)

Частное решение этого уравнения имеет вид:

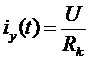. (2.20)

Однородное уравнение получают из (2.19) с учетом до коммутационных начальных условий:

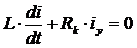. (2.21)

Общим решением (2.21) является показательная функция вида ,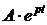

причем А – постоянный коэффициент, p – корень характеристического уравнения.

.

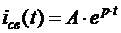Так как при U = 0 i_у = 0, то выражение (11.6) принимает вид

R_к + L∙P = 0,

откуда

.

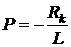Переходный ток определяется как сумма составляющих:

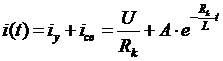. (2.22)

Согласно первому закону коммутации при t = 0 ток i(t) также равен нулю. Поэтому (2.22) приходит к виду

,

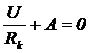откуда

.

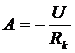Подставляя значение А в (2.22) получаем окончательное решение:

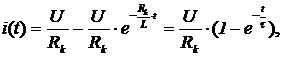(2.23)

где τ = L/R_к – постоянная цепи.

Графики i(t), u_L(t) и u_R(t) приведены на рис. 2.15.

Напряжение на резистивном элементе пропорционально току (рис. 2.15, б)

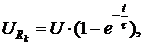
а на индуктивности

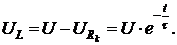
2.3. Отключение индуктивности от источника

постоянного напряжения

Рассмотрим переходный процесс при отключении источника постоянного напряжения от цепи рис. 2.16. Допустим, что ключ К находится в положении 1 достаточно долго, так, что цепь перешла в установившейся режим. В установившемся режиме сила тока ограничена только сопротивлением провода катушки индуктивности – R_к, и равна 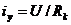. Переведем ключ К в положение .

Согласно закону коммутации ток через индуктивность после отключения источника остается равным i_у = 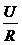. Выражение (2.21) принимает вид:

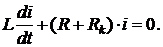
Так как источник отсутствует, принужденной составляющей тока нет. В цепи протекает только свободная составляющая тока

,

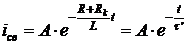где τ′ = L/(R + R_k) – постоянная цепи после переключения ключа К, А = i₀.

Если R = n∙R_k, то падение напряжения на нем в первый момент после коммутации окажется в n раз больше напряжения источника. Такой бросок напряжения может привести к аварийной ситуации в цепи. Это следует иметь в виду при проектировании, расчете и эксплуатации цепей с индуктивностью.

2.4. Подключение индуктивности к источнику

синусоидального напряжениия

Пусть в цепь с индуктивностью включён источник синусоидального напряжения u(t) = U_m·sin (ωt + ψ_u) (Рис. 2.17).

Установившийся ток определяется выражением:

i_у = I_m·sin (ωt + ψ_u - φ).

Свободная составляющая переходного тока имеет тот же вид, что и для цепи с источником постоянного напряжения:

.

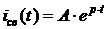Переходный ток в цепи

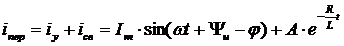. (2.24)

С учётом начальных условий, при t = 0 i_пер = 0 и (2.24) принимает вид

.

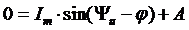Отсюда

,

,

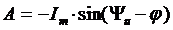а

.

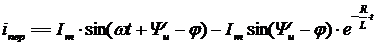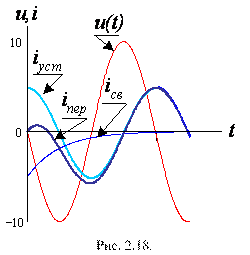
Графики зависимости от времени напряжения источника u, установившегося i_у, свободного i_св и переходного i_пер токов приведены на рис. 2.18. Они показывают, что начальное значение свободного тока зависит от момента включения, т. е. от начальной фазы напряжения – ψ_u. Если ψ_u – φ = 0, то i_св = 0. В этом случае коммутация не повлечётпереходного процесса. Сразу же после включения переходный ток будет равен установившемуся

i_у = I_m·sin (ωt + ψ_u - φ).

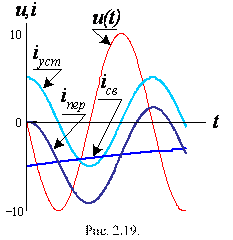
При ψ_u – φ ≠ 0 имеет место переходный режим, при котором в определенную часть периода установившийся и свободный токи имеют одинаковые знаки. Разница между i_пер и i_у зависит от начального значения и постоянной τ. При условии ψ_i = ψ_u – φ = 90° начальное значение свободного тока максимально и равно I_m. Если τ значительно больше периода напряжения и при ψ_i = ψ_u – φ = 90° максимальное значение переходного тока может почти в два раза превысить амплитуду установившегося тока (рис. 2.19).

КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ

2.1. Как определяются знаки членов уравнений, составленных:

а) по первому закону Кирхгофа,

б) по второму закону Кирхгофа?

2.2. Составьте уравнения по первому закону Кирхгофа для всех узлов схемы рис. 2.7, б.

2.3. Составьте уравнения по второму закону Кирхгофа для всех контуров схемы рис. 2.6, б.

2.4. Какое соединение участков электрической цепи называется последовательным? Приведите соотношение для эквивалентного сопротивления цепи из n последовательно соединенных сопротивлений.

2.5. Какое соединение участков электрической цепи называется параллельным? Приведите соотношение для эквивалентного сопротивления цепи из n параллельно соединенных сопротивлений.

2.6. Приведите схемы соединений треугольником и звездой. Определите значение элементов эквивалентного соединения треугольником, если в схеме рис. 2.4, а R₁ = R₂ = R₃ = 10 Ом.

2.7. В каких случаях возможно и целесообразно применять к анализу электрических цепей метод эквивалентных преобразований? В чем состоит суть этого метода?

2.8. В схеме рис. 2.6, б определите значение источника Э.Д.С. Е, если известно, что R₁ = R₃ =2 Ом, R₂ = R_4,5 = 10 Ом, а I₃ = 2 А.

2.9. В каких случаях целесообразно применение метода контурных токов? Как определяются значения контурных сопротивлений и контурных Э.Д.С., взаимных сопротивлений?

2.10. В чем состоит суть междуузлового метода анализа электрической цепи? Как определяются знаки Э.Д.С. в выражении для междуузлового напряжения?

2.11. Определите U_АВ и токи всех ветвей схемы рис. 2.8, в, если известно: Е₁ = 10 В; R₁ = 2 Ом, R₂ = 10 Ом,а R₃ = 20 Ом.

2.12. Для каких случаев расчета электрических цепей применяется метод активного эквивалентного двухполюсника?

2.13. Сформулируйте правила определения параметров активного эквивалентного двухполюсника.

2.14. В схеме рис. 2.6, б известно: Е = 32,8 В, R1 = R3 = 2 Ом, а R2 = R4,5 = 10 Ом. Определите ток I₃ методом активного эквивалентного двухполюсника.

2.15. В схеме рис. 2.11 известно: Е = 10 В, R_к = 2 Ом, R = 20 Ом, а L = 0,1 Гн. Постройте график изменения тока цепи после замыкания ключа К до установившегося значения. Определите бросок напряжения на резистре R в момент размыкания ключа К после установившегося режима.