Движение заряженной частицы в магнитном поле
 Если частица с электрическим зарядом q и массой m влетает со скоростью
Если частица с электрическим зарядом q и массой m влетает со скоростью 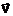 в магнитное поле с индукцией
в магнитное поле с индукцией 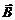 , то на нее начинает действовать сила Лоренца
, то на нее начинает действовать сила Лоренца
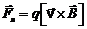 , (7.1)
, (7.1)
которая перпендикулярна скорости частицы 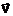 и индукции
и индукции 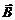 . Это приводит к искривлению траектории без изменения скорости частицы (так как сила Лоренца не совершает работу).
. Это приводит к искривлению траектории без изменения скорости частицы (так как сила Лоренца не совершает работу).
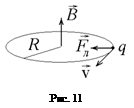
Рассмотрим ситуацию, когда частица влетает в магнитное поле перпендикулярно индукции 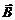 . В этом случае она будет двигаться по окружности с постоянной скоростью, а сила Лоренца будет являться центростремительной силой (см. рис.11).
. В этом случае она будет двигаться по окружности с постоянной скоростью, а сила Лоренца будет являться центростремительной силой (см. рис.11).
Найдем радиус окружности, используя второй закон Ньютона:
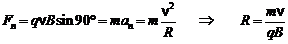 (7.2)
(7.2)
Используя формулу (7.2), можно рассчитать период вращения частицы по окружности:
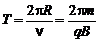 (7.3)
(7.3)
Задача 10
 В однородном магнитном поле с индукцией В = 1 Тл по окружности летает положительно заряженная частица с зарядом q = 1 мкКл и массой m = 10–10кг со скоростью v = 10 км/с. Индукция магнитного поля
В однородном магнитном поле с индукцией В = 1 Тл по окружности летает положительно заряженная частица с зарядом q = 1 мкКл и массой m = 10–10кг со скоростью v = 10 км/с. Индукция магнитного поля 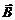 направлена вдоль оси z. В начальный момент времени скорость частицы
направлена вдоль оси z. В начальный момент времени скорость частицы 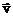 была направлена вдоль оси у. Найти минимальное время t, через которое скорость частицы будет направлена а) вдоль оси х; б) против оси х. Найти пройденный путь за это время.
была направлена вдоль оси у. Найти минимальное время t, через которое скорость частицы будет направлена а) вдоль оси х; б) против оси х. Найти пройденный путь за это время.
Решение:
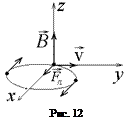
Из векторного выражения (7.1) следует, что сила Лоренца, действующая на частицу в начальный момент времени направлена вдоль оси х, поэтому частица будет двигаться так, как показано на рис.12. Из этого рисунка следует, что через четверть оборота или через время 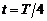 скорость частицы окажется направленной параллельно оси х, а через три четверти периода (
скорость частицы окажется направленной параллельно оси х, а через три четверти периода ( 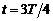 ) – антипараллельно оси х. Используя формулу для радиуса окружности (7.2) и периода (7.3), получаем ответ:
) – антипараллельно оси х. Используя формулу для радиуса окружности (7.2) и периода (7.3), получаем ответ:
а) 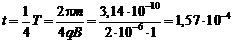 с;
с;
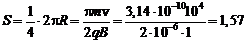 м.
м.
б) 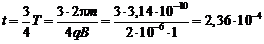 с
с
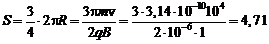 м.
м.
Ответы: а) t = 0,157 мс; S = 1,57 м; б) t = 0,236 мс; S = 4,71 м.
Задача 11
 В однородном магнитном поле с индукцией В = 1 Тл по окружности летает отрицательно заряженная частица с зарядом q = – 1 мкКл и массой m = 10–10кг со скоростью v = 20 км/с. Индукция магнитного поля
В однородном магнитном поле с индукцией В = 1 Тл по окружности летает отрицательно заряженная частица с зарядом q = – 1 мкКл и массой m = 10–10кг со скоростью v = 20 км/с. Индукция магнитного поля 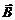 направлена вдоль оси х. В начальный момент времени скорость частицы
направлена вдоль оси х. В начальный момент времени скорость частицы 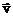 была направлена вдоль оси у. Найти минимальное время t, через которое скорость частицы будет направлена а) вдоль оси z; б) против оси z. Найти пройденный путь за это время.
была направлена вдоль оси у. Найти минимальное время t, через которое скорость частицы будет направлена а) вдоль оси z; б) против оси z. Найти пройденный путь за это время.
Решение:
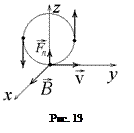
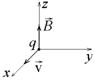
Из векторного выражения (7.1) следует, что сила Лоренца, действующая на частицу в начальный момент времени направлена вдоль оси z, поэтому частица будет двигаться так, как показано на рис.13 Из этого рисунка следует, что через четверть оборота или через время 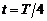 скорость частицы окажется направленной параллельно оси z, а через три четверти периода (
скорость частицы окажется направленной параллельно оси z, а через три четверти периода ( 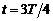 ) – антипараллельно оси z. Используя формулу для периода (7.3), получаем ответ:
) – антипараллельно оси z. Используя формулу для периода (7.3), получаем ответ:
а) 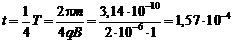 с;
с;
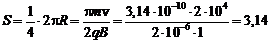 м.
м.
б) 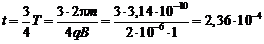 с
с
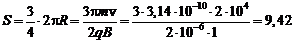 м.
м.
Ответы: а) t = 0,157 мс; S = 3,14 м; б) t = 0,236 мс; S = 9,42 м.
Плоский конденсатор
Разность потенциалов на обкладках плоского конденсатора, расстояние между которыми равно d и напряженность электрического поля Е:
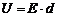 . (8.1)
. (8.1)
Энергия электрического поля в плоском конденсаторе, где С – емкость конденсатора, q – заряд на конденсаторе, U – напряжение на конденсаторе, Е – напряженность электрического поля:
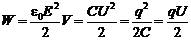 (8.2)
(8.2)
Напряженность однородного электрического поля внутри плоского конденсатора. 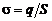 – поверхностная плотность заряда на обкладках плоского конденсатора:
– поверхностная плотность заряда на обкладках плоского конденсатора:
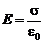 . (8.3)
. (8.3)
Уравнения Максвелла
Переменное магнитное поле с индукцией 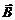 порождает в пространстве вихревое электрическое поле с напряженностью
порождает в пространстве вихревое электрическое поле с напряженностью 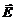 :
:
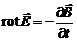 . (9.1)
. (9.1)
Вихревое магнитное поле с напряженностью 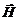 порождается в пространстве токами проводимости с плотностью
порождается в пространстве токами проводимости с плотностью 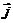 и переменным электрическим полем с индукцией
и переменным электрическим полем с индукцией 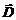 :
:
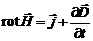 . (9.2)
. (9.2)
Материальное уравнение связывает вектор 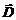 и
и 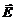 в изотропном диэлектрике:
в изотропном диэлектрике:
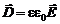 , (9.3)
, (9.3)
где e – диэлектрическая проницаемость среды ( 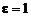 для воздуха),
для воздуха),
e0 = 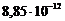 Ф/м– электрическая постоянная.
Ф/м– электрическая постоянная.
Задача 12
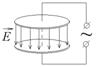 Между обкладками плоского воздушного конденстатора создано однородное электрическое поле, напряженность которого меняется со временем по закону
Между обкладками плоского воздушного конденстатора создано однородное электрическое поле, напряженность которого меняется со временем по закону 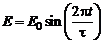 . Найти модуль ротора напряженности магнитного поля (или плотность тока смещения) внутри конденсатора в момент времени t = 1 с, если
. Найти модуль ротора напряженности магнитного поля (или плотность тока смещения) внутри конденсатора в момент времени t = 1 с, если 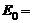 1 кВ/м;
1 кВ/м; 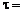 1 с.
1 с.
Решение:
Между обкладками конденсатора нет токов проводимости, т.е. 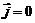 . Так как конденсатор воздушный, то диэлектрическая проницаемость среды e = 1, следовательно из формулы (9.3)
. Так как конденсатор воздушный, то диэлектрическая проницаемость среды e = 1, следовательно из формулы (9.3) 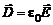 . По формуле (9.2) найдем модуль ротора
. По формуле (9.2) найдем модуль ротора 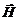 в момент времени t = 1 c:
в момент времени t = 1 c:
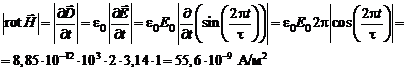
Ответ: 55,6 нА/м2
Задача 13
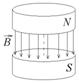 Между полюсами магнита создано однродное магнитное поле, индукция которого зависит от времени по закону
Между полюсами магнита создано однродное магнитное поле, индукция которого зависит от времени по закону 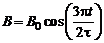 . Найти модуль ротора напряженности электрического поля между полюсами в момент времени t = 1 с, если
. Найти модуль ротора напряженности электрического поля между полюсами в момент времени t = 1 с, если 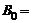 1 Тл;
1 Тл; 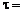 1 с.
1 с.
Решение:
По формуле (9.1) найдем модуль ротора 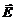 :
:
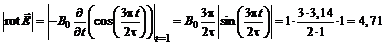 Тл/с
Тл/с
Ответ: 4,71 Тл/с
 10. Электрические колебания
10. Электрические колебания
Уравнение затухающих колебаний в контуре, состоящем из последовательно соединенных резистора с сопротивлением R, конденсатора с емкостью С и катушки с индуктивностью L, выглядит так:
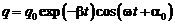 , (10.1)
, (10.1)
где b – коэффициент затухания:
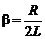 ; (10.2)
; (10.2)
w –– циклическая частота собственных затухающих колебаний.
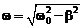 ; (10.3)
; (10.3)
w0 – циклическая частота собственных незатухающих колебаний.
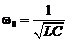 (10.4)
(10.4)
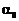 – начальная фаза колебаний,
– начальная фаза колебаний, 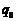 – начальная амплитуда.
– начальная амплитуда.
Амплитуда колебаний в контуре уменьшается со временем по закону:
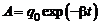 . (10.5)
. (10.5)
q – логарифмический декремент затухания:
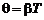 . (10.6)
. (10.6)
t –– время релаксации (время, за которое амплитуда уменьшится в е = 2,72 раз)
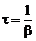 . (10.7)
. (10.7)
Задача 14
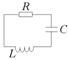 В контуре совершаются свободные слабозатухающие колебания, при которых заряд на конденсаторе изменяется во времени по закону
В контуре совершаются свободные слабозатухающие колебания, при которых заряд на конденсаторе изменяется во времени по закону 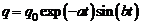 . Оцените время, через которое энергия контура уменьшится в 2раза.
. Оцените время, через которое энергия контура уменьшится в 2раза. 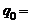 1 мкКл;
1 мкКл; 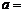 0,05 с–1;
0,05 с–1; 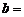 10 c–1. Каким станет коэффициент затухания, если:
10 c–1. Каким станет коэффициент затухания, если:
а) сопротивление R в контуре увеличить в 2 раза?
б) индуктивность L в контуре увеличить в 2 раза?
в) емкость С в контуре увеличить в 2 раза?
Решение:
Энергия контура W пропорциональна квадрату амплитуды колебаний, поэтому, используя формулу (10.5) и учитывая, что b = а = 0,05 с–1, получим:
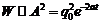 (10.8)
(10.8)
Найдем отношение энергий контура в начальный момент времени и в момент времени t:
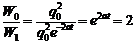 . (10.9)
. (10.9)
Из формулы (10.9) видно, что 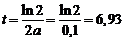 с
с
из формулы (10.2) следует, что
а) если сопротивление в контуре увеличить в два раза, то коэффициент затухания увеличится также в два раза: 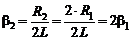 = 0,1 с–1;
= 0,1 с–1;
б) при изменении индуктивности в два раза, коэффициент затухания уменьшится в два раза: 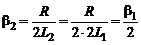 = 0,025 с–1;
= 0,025 с–1;
в) при изменении емкости в два раза коэффициент затухания не изменится, так как он не зависит от емкости С (см. формулу (10.2)).
Ответы:t = 6,93 c; а) b = 0,1 с–1; б) b = 0,025 с–1; в) b = 0,05 с–1.
