Теорема о циркуляции вектора индукции магнитного поля.
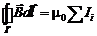 (4.1)
(4.1)
– циркуляция по замкнутому контуру вектора индукции магнитного поля равна алгебраической сумме сил токов, пронизывающих поверхность S, ограниченную контуром, умноженной на магнитную постоянную 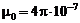 Гн/м. Cила тока считается положительной, если направление тока в точке пересечения с поверхностью S совпадает с направлением положительной нормали к поверхности в этой точке, и отрицательный, если направление тока противоположно направлению этой нормали. Положительная нормаль определяется по правилу правого винта по отношению к направлению обхода Г (см. рис.6).
Гн/м. Cила тока считается положительной, если направление тока в точке пересечения с поверхностью S совпадает с направлением положительной нормали к поверхности в этой точке, и отрицательный, если направление тока противоположно направлению этой нормали. Положительная нормаль определяется по правилу правого винта по отношению к направлению обхода Г (см. рис.6).
Если один из токов охватывается контуром N раз, то в формуле (4.1) такой ток будет складываться N раз.
Задача 6
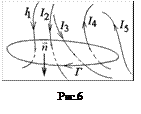 По длинным проводам различной конфигурации текут разные токи (см. рис.6). Найдите циркуляцию вектора индукции магнитного поля, созданного этими токами, по замкнутому контуру Г.
По длинным проводам различной конфигурации текут разные токи (см. рис.6). Найдите циркуляцию вектора индукции магнитного поля, созданного этими токами, по замкнутому контуру Г.
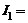 1 А,
1 А, 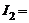 2 А,
2 А, 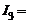 3 А,
3 А, 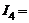 4 А,
4 А, 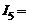 5 А.
5 А.
Решение:
Нарисуем вектор нормали 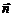 в соответствии с обходом Г по правилу правого винта (см. рис.6). Таким образом можно определить знак каждой силы тока, входящей в формулу (4.1) и найти циркуляцию:
в соответствии с обходом Г по правилу правого винта (см. рис.6). Таким образом можно определить знак каждой силы тока, входящей в формулу (4.1) и найти циркуляцию:
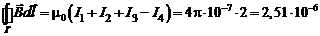 Тл×м
Тл×м
В этом примере учтено, что ток 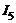 не пронизывает контур, поэтому и не входит в алгебраическую сумму в формуле (4.1)
не пронизывает контур, поэтому и не входит в алгебраическую сумму в формуле (4.1)
Ответ: 2,51 мкТл×м.
Диполи в электрическом и магнитном полях.
Система из двух одинаковых по модулю, но разных по знаку электрических зарядов q, находящихся на очень малом расстоянии друг от друга l (по сравнению с расстоянием до точки наблюдения r), называется диполем. Диполь характеризуется электрическим моментом 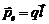 , где
, где 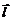 – вектор, направленный из отрицательного заряда к положительному. Диполь, взаимодействуя с электрическим полем, обладает потенциальной энергией взаимодействия
– вектор, направленный из отрицательного заряда к положительному. Диполь, взаимодействуя с электрическим полем, обладает потенциальной энергией взаимодействия
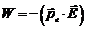 (5.1)
(5.1)
Стремясь занять в пространстве положение с наименьшей потенциальной энергией (5.1), диполь разворачивается своим моментом вдоль напряженности поля 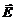 . В неоднородном электрическом поле на такой диполь действует сила
. В неоднородном электрическом поле на такой диполь действует сила
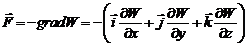 , (5.2)
, (5.2)
которая стремится втянуть диполь в область с большей напряженностью.
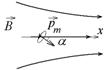
Небольшой виток площадью S с током I обладает магнитным моментом 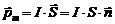 , который направлен вдоль положительной нормали
, который направлен вдоль положительной нормали 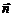 , определяемой по правилу правого винта относительно направления тока по этому витку. Такой магнитный момент, взаимодействуя с внешним магнитным полем с индукцией
, определяемой по правилу правого винта относительно направления тока по этому витку. Такой магнитный момент, взаимодействуя с внешним магнитным полем с индукцией 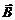 , обладает энергией взаимодействия
, обладает энергией взаимодействия
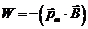 (5.3)
(5.3)
Аналогично электрическому диполю магнитный диполь также стремится принять положение с минимальной энергией (5.3) и разворачивается своим моментом вдоль поля 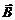 , а в неоднородном магнитном поле на него действует сила (5.2), втягивающая такой виток в область с бόльшими значениями
, а в неоднородном магнитном поле на него действует сила (5.2), втягивающая такой виток в область с бόльшими значениями 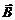 .
.
Задача 7
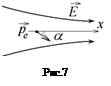 Электрический диполь с дипольным моментом
Электрический диполь с дипольным моментом 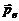 , удерживают в неоднородном электрическом поле на оси х под углом a к ней в точке с координатой
, удерживают в неоднородном электрическом поле на оси х под углом a к ней в точке с координатой 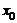 . Определите проекцию силы
. Определите проекцию силы 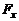 , действующей на диполь, если напряженность электрического поля на оси х меняется по закону
, действующей на диполь, если напряженность электрического поля на оси х меняется по закону 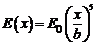 ,
,
где 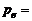 1 Кл×м;
1 Кл×м; 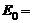 1 В/м; b = 1 м;
1 В/м; b = 1 м; 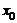 = 1 м; a = 60°.
= 1 м; a = 60°.
Решение:
По формуле (5.1) найдем зависимость энергии взаимодействия диполя и электрического поля:
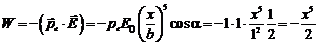
Из формулы (5.2) найдем проекцию силы на ось х в точке 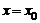 :
:
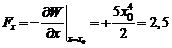 Н
Н
Ответ: 2,5 Н
 6. Э.Д.С. индукции и самоиндукции
6. Э.Д.С. индукции и самоиндукции
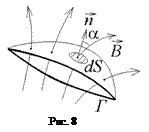 Рассмотрим замкнутый контур Г произвольной формы в неоднородном магнитном поле, который ограничивает некоторую поверхность S (см. рис.8). Потоком индукции магнитного поля сквозь эту поверхность называется величина
Рассмотрим замкнутый контур Г произвольной формы в неоднородном магнитном поле, который ограничивает некоторую поверхность S (см. рис.8). Потоком индукции магнитного поля сквозь эту поверхность называется величина
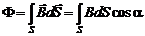 , (6.1)
, (6.1)
где a – угол между вектором 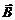 и нормалью
и нормалью 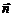 к площадке поверхности dS, которую магнитное поле пронизывает.
к площадке поверхности dS, которую магнитное поле пронизывает.
При изменении потока Ф во времени в контуре Г возникает Э.Д.С. индукции – электродвижущая сила, равная скорости изменения магнитного потока (закон электромагнитной индукции Фарадея):
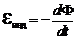 (6.2)
(6.2)
Если бы контур был сделан из проводящего вещества, то по нему потек бы электрический ток.
Поток Ф может изменяться по следующим причинам.
1) Изменяется индукция магнитного поля 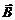 .
.
2) Изменяются геометрические размеры контура, т.е. изменяется площадь S.
3) Изменяется ориентация контура в пространстве, т.е. изменяется угол a.
В случае 1) в пространстве возникает вихревое электрическое поле 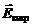 , действующее на свободные электроны проводящего контура.
, действующее на свободные электроны проводящего контура.
В случаях 2) и 3) из-за перемещения проводника в магнитном поле на свободные электроны в нем действует сила Лоренца.
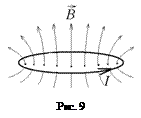 Если рассмотреть контур, по которому протекает ток I (см. рис.9), то индукция
Если рассмотреть контур, по которому протекает ток I (см. рис.9), то индукция 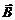 порождаемого этим током магнитного поля создает сквозь поверхность контура поток, пропорциональный силе тока I:
порождаемого этим током магнитного поля создает сквозь поверхность контура поток, пропорциональный силе тока I:
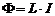 , (6.3)
, (6.3)
где коэффициент пропорциональности L называется индуктивностью контура. Если ток в контуре начинает изменяться, то в нем возникнет Э.Д.С. самоиндукции:
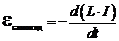 (6.4)
(6.4)
Знак "–" в формулах (6.2) и (6.4) означает, что при изменении магнитного потока сквозь замкнутый контур в нем возникает такая Э.Д.С., которая стремится уменьшить изменение потока.Это правило Ленца.В результате увеличения силы тока на рис. 9, а следовательно и индукции 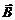 , возникает вихревое электрическое поле, направленное против тока I в контуре.
, возникает вихревое электрическое поле, направленное против тока I в контуре.
Задача 8
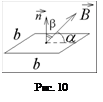 Квадратный проводящий контур со стороной b = 1 м пронизывает однородное магнитное поле под углом a = 30° к плоскости контура. Индукция магнитного поля меняется со временем по закону
Квадратный проводящий контур со стороной b = 1 м пронизывает однородное магнитное поле под углом a = 30° к плоскости контура. Индукция магнитного поля меняется со временем по закону 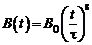 . Найти модуль э.д.с. индукции в контуре в момент времени t = 1 с, если
. Найти модуль э.д.с. индукции в контуре в момент времени t = 1 с, если 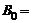 1 Тл; t = 1 с.
1 Тл; t = 1 с.
Решение:
Определим зависимость магниного потока от времени:
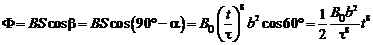
По формуле (6.2) определим модуль Э.Д.С. индукции:
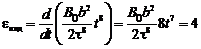 В
В
Ответ: 4 В
Задача 9
По проводящему контуру индуктивностью L течет ток I. Найти модуль э.д.с. самоиндукции в контуре в момент времени t = 1 с, если и ток и индуктивность изменяются со временем по законам 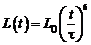 ,
, 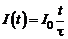 , где
, где 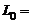 1 Гн;
1 Гн; 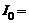 1А; t = 1 с.
1А; t = 1 с.
Решение:
Воспользуемся формулой (6.4):
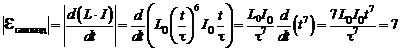 В.
В.
Ответ: 7 В.
