Математическая обработка результатов эксперимента
Прямые измерения[7]
1. Вычислить выборочное среднее из N измерений[8]:
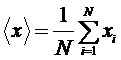 . (1)
. (1)
2. Вычислить выборочное стандартное отклонение среднего:
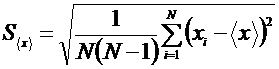 . (2)
. (2)
3. Вычислить абсолютную погрешность (значение 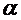 задает преподаватель):
задает преподаватель):
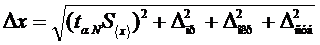 , (3)
, (3)
где 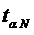 - коэффициент Стьюдента (см. табл. 3 стр. 50), для заданного
- коэффициент Стьюдента (см. табл. 3 стр. 50), для заданного 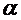 и N (N- число измерений),
и N (N- число измерений), 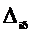 -приборная погрешность,
-приборная погрешность, 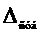 - субъективная погрешность. Эти погрешности определяются:
- субъективная погрешность. Эти погрешности определяются:
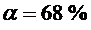 | 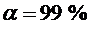 |
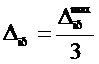 | 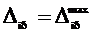 |
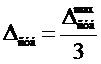 | 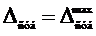 |
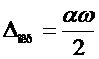 , где , где 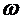 - цена деления (определяется по шкале прибора) - цена деления (определяется по шкале прибора) |
Числовые значения 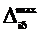 ,
, 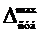 для конкретных приборов, используемых в выполняемой лабораторной работе, берутся из табл. 1 (см. стр. 46).
для конкретных приборов, используемых в выполняемой лабораторной работе, берутся из табл. 1 (см. стр. 46).
4. Определить относительную погрешность:
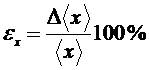 . (4)
. (4)
5. Результат записать в виде ( подробнее см. ниже «Запись результатов вычислений»):
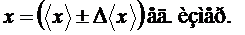 ,
, 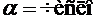 . (5)
. (5)
Косвенные измерения[9]
1. Предварительно произвести расчет погрешностей прямых измерений (см. выше) (погрешности табличных значений стр. 49), результат записать в виде (5).
2. Вычислить среднее значение 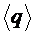 (величина q есть функция
(величина q есть функция 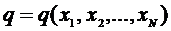 ) в соответствии с расчетной формулой.
) в соответствии с расчетной формулой.
3. Вычислить абсолютную погрешность 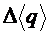 :
:
А) Универсальный метод:
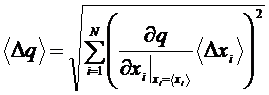 . (6)
. (6)
Например:
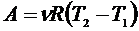 , где
, где 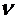 , R,
, R, 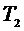 ,
, 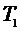 - результаты прямых измерений, для которых известны абсолютные погрешности
- результаты прямых измерений, для которых известны абсолютные погрешности 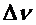 ,
, 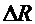 ,
, 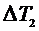 ,
, 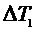 .
.
Воспользуемся формулой (6):
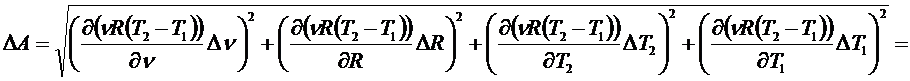
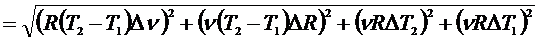 .
.
Б) Если величина q может быть представлена в виде: 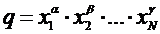 , где
, где 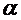 ,
, 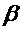 ,
, 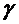 - точные числа, тогда абсолютную погрешность можно определить более просто по формуле:
- точные числа, тогда абсолютную погрешность можно определить более просто по формуле:
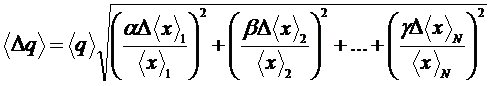 . (7)
. (7)
Например:
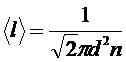 , где
, где 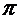 - табличное значение,
- табличное значение, 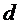 ,
, 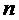 - результаты прямых измерений, для которых известны абсолютные погрешности
- результаты прямых измерений, для которых известны абсолютные погрешности 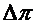 ,
, 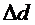 ,
, 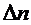 .
.
Перепишем заданную формулу в виде: 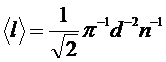 .
.
Воспользуемся формулой (7):
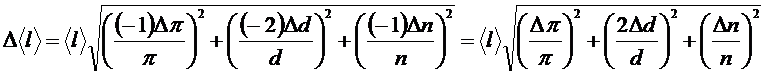 .
.
С) Метод «Шаг за шагом»:
В некоторых случаях вычисление частных производных формулы (6) может быть достаточно сложным, при этом формула (7) может оказаться не применима, т.к. q есть функция, в которую входит разность или сумма. Тогда исходную формулу можно разбить на части, используя дополнительные обозначения.
Например:
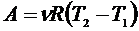 , где
, где 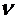 , R,
, R, 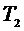 ,
, 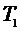 - результаты прямых измерений, для которых известны абсолютные погрешности
- результаты прямых измерений, для которых известны абсолютные погрешности 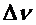 ,
, 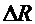 ,
, 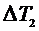 ,
, 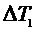 .
.
Обозначим 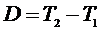 , тогда
, тогда 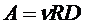 или
или 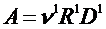 . Выражение для
. Выражение для 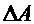 получаем, применяя формулу (7):
получаем, применяя формулу (7):
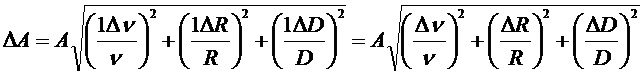 .
.
Выражение для 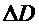 получаем, применяя формулу (6):
получаем, применяя формулу (6):
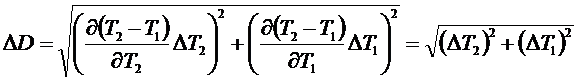 .
.
4. Результат записать в виде (см. ниже «Запись результатов вычислений»):
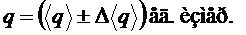 ,
, 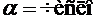 . (8)
. (8)
5. Определить относительную погрешность:
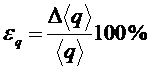 . (9)
. (9)
Запись результатов вычислений
Конечный результат вычислений при выполнении лабораторной работы записывается в виде (5), (8), при этом среднее значение записывается в стандартном виде, значение абсолютной погрешности (напр. 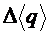 ) округляется до одной или двух значащих цифр[10].
) округляется до одной или двух значащих цифр[10].
Значащими называются все цифры числа, начиная с первой слева, отличной от нуля.
Например:
В числе 0,0320 значащими цифрами будут три цифры 3, 2, правый 0, тогда, округляя до двух значащих цифр,- 0,032 .
В числе 1245 значащими цифрами будут четыре цифры, тогда, округляя до двух значащих цифр,- 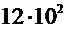 .
.
В среднем значении (напр. 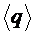 ) оставляют все верные и одну неверные цифры (округляя по правилам математики).
) оставляют все верные и одну неверные цифры (округляя по правилам математики).
