Определение универсальной газовой постоянной методом откачки
Цель работы: определение универсальной газовой постоянной (R) одинаковой для всех идеальных газов.
Теоретическая часть
Универсальную газовую постоянную можно определить, используя уравнение Менделеева-Клапейрона:
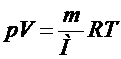, (1)
где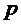 
– давление газа, V– объем газа, m– масса газа, M– молярная масса газа, Т–абсолютная температура газа. Все параметры газа, входящие в уравнение (1), можно измерить непосредственно, за исключением массы газа, т.к. взвешивание газа возможно только вместе с сосудом, в который он заключен, поэтому для определения массы газа (m)необходимо исключить массу сосуда. Это можно сделать, рассмотрев два состояния одного и того же газа при неизменных температуре (Т) и объеме (V). Пусть в первом состоянии масса газа 
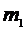, а во втором 
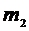. Масса сосуда с воздухом в первом состоянии 
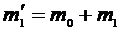, где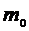 
– масса сосуда, а масса сосуда во втором состоянии 
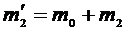, очевидно, что 
.
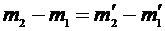Записав уравнение (1) для двух состояний газа, получаем систему из двух уравнений, решение которой дает выражение для универсальной газовой постоянной:
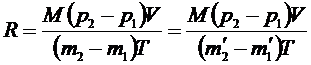. (2)
Таким образом, для определения универсальной газовой постоянной необходимо определить разность масс сосуда с воздухом при атмосферном давлении и после откачки-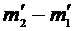 
, и остальные величины в формуле (2).
Экспериментальная часть
Описание установки
Схематический вид установки показан на рис. 1. Установка состоит из металлического баллона (1) объемом V, имеющего вакуумный кран (2) (кран (2) на рис. 1 показан в положении «Закрыто») и штуцер (3). С помощью резинового шланга (8) баллон можно соединить с откачивающей системой, которая состоит из механического вакуумного насоса (4), стрелочного манометра (манометр Бурдона) (5), укороченного ртутного манометра (6) и распределительного вакуумного крана (7).
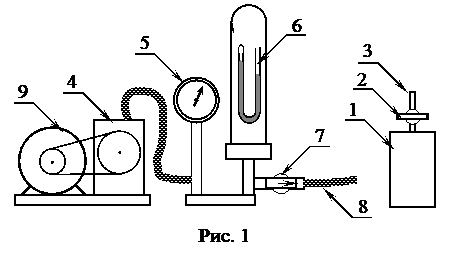Вакуумный насос приводится в действие электромотором (9). В комплект приборов входят также барометр-анероид, технические весы и термометр.
Выполнение работы
1. Соединить баллон (1) с откачивающей системой при помощи шланга (8). Открыть кран (2) на баллоне, для этого ручку крана (2) установить параллельно штуцеру (3). Распределительный кран (7) повернуть так, чтобы стрелка на нем была направлена в сторону баллона. Включить мотор насоса и следить за откачкой баллона по манометрам (5) и (6).
2. После того, как на укороченном ртутном манометре (6) установится постоянная разность уровней, определяемая предельным разрежением насоса (4), записать показания этого манометра, разность которых будет соответствовать давлению воздуха в баллоне после откачки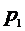 
. Закрыть кран (2) на баллоне, повернув его на угол 90°. Выключить мотор насоса.
3. Запустить воздух в насос, повернув распределительный кран (7) стрелкой от баллона. Следить за поведением манометров. После того, как стрелка манометра Бурдона (5) вернется на «0», отсоединить баллон от откачивающей системы.
4. Определить массу баллона с воздухом после откачки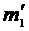 
, используя технические весы. (Перед измерениями подставка весов выставляется по отвесу вращением регулировочных ножек. Смотри рис. 2.) Определите цену деления нагруженных технических весов.
5. Включив арретир на весах, не снимая разновесов с чаши весов, аккуратно снять баллон с чаши весов. Открыть кран (2) на баллоне и запустить воздух в баллон. Далее аккуратно вернуть баллон на чашу весов и добавлением разновесов вновь уравновесить весы, т.е. определить массу баллона с воздухом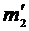 
.
6. Определить давление в баллоне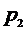 
, которое при открытом кране (2) равно атмосферному давлению и определяется с помощью барометра в аудитории. Определить температуру воздуха в баллоне (T), считая ее равной комнатной температуре.
7. Вычислить универсальную газовую постоянную (R) по формуле (2), учитывая, что молярная масса воздуха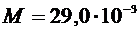 
кг/моль. Значение объема баллона (V) указано на баллоне.
8. Рассчитать абсолютную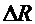 
и относительную 
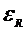погрешности. Записать окончательный результат и сравнить его с табличным с учетом погрешности.
Контрольные вопросы
1. Пояснить физический смысл универсальной газовой постоянной.
2. Назвать возможные процессы в газах, записать уравнения этих процессов, построить их диаграммы.
3. Дать определение моля и молярной массы вещества.
4. Объяснить устройство и принцип действия механических ротационных вакуумных насосов (форвакуумные насосы).
5. Объяснить устройство и принцип действия манометров, используемых в работе.
6. Объяснить устройство и принцип действия барометра-анероида.
Литература
1. Лабораторный практикум по физике. Под ред. Ахматова А.С. М.: 1980.
2. Кикоин И.К., Кикоин А.К. Молекулярная физика. M.: 1963.
3. Савельев И.В. Курс общей физики. Т. I. М.: 1977.
4. Физический энциклопедический словарь. М.: 1990.
Лабораторная работа № 3
Определение отношения теплоемкостей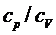 
для воздуха методом Клемана-Дезорма
Цель работы: определение отношения теплоемкости воздуха при постоянном давлении к теплоемкости воздуха при постоянном объеме методом Клемана-Дезорма.
Теоретическая часть
Теплоемкостью тела (С)называют количество теплоты, необходимое для его нагревания на 1 К:
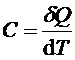. (1)
Величина Сзависит от массы тела, его химического состава и процесса, в котором сообщается теплота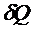 
.
Теплоемкость единицы массы вещества (с) называют удельной теплоемкостью вещества:
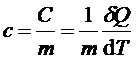, (2)
где m - масса тела.
Молярной теплоемкостью (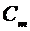 
) называют теплоемкость одного моля вещества:
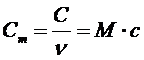, (3)
где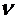 
- количество вещества, M- молярная масса вещества.
Если нагревать тело при постоянном объеме, то все тепло, сообщаемое телу извне, полностью идет на увеличение внутренней энергии. Если нагревать тело при постоянном давлении, то сообщенное тепло идет не только на увеличение внутренней энергии, но и на работу изобарического расширения. Поэтому теплоемкость при постоянном давлении (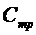 
) должна быть больше, чем теплоемкость при постоянном объеме ( 
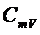). Эти теплоемкости особенно сильно различаются у газов вследствие относительно большого коэффициента объемного расширения.
Молярные теплоемкост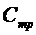и и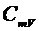 
идеального газа связаны уравнением Мейера:
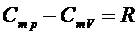, (4)
где R- универсальная газовая постоянная. Для удельных теплоемкосте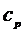й 
и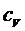 
уравнение Майера примет вид:
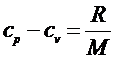. (5)
Отношение теплоемкостей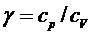 
принадлежит к числу весьма важных термодинамических величин.
В настоящей работе определение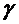 
производится одним из классических методов, методом Клемана-Дезорма, основанном на исследовании некоторой массы газа, последовательно проходящего через три состояния. Клеман и Дезорм предложили и осуществили этот метод в 1819 году.
Стеклянный баллон вместимостью в несколько литров (рис. 1) наполняется воздухом при атмосферном давлении. С помощью компрессора в баллон дополнительно накачивается небольшая порция воздуха, затем кран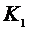 
закрывается. Спустя короткое время температура газа в баллоне сравняется с температурой 
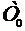в аудитории - состояние (1). После этого жидкостным манометром измеряют давление газа в баллоне:
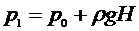, (6)
где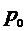 
- атмосферное давление, 
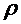- плотность жидкости в манометре, 
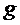- ускорение свободного падения, H- разность уровней жидкости в манометре.
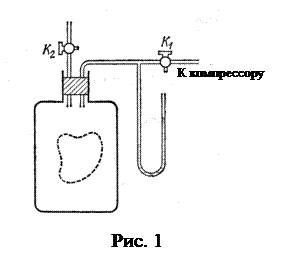Затем на короткое время открывают кран 
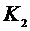, газ в баллоне адиабатически расширяется, его давление сравняется с атмосферным 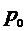, при этом часть газа выходит из баллона. Газ в баллоне при расширении совершает работу против давления окружающего воздуха, и вследствие этого его температура понизится до некоторого значения 
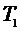- состояние (2) .
Затем кран 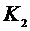быстро закрывается, и газ начинает медленно нагреваться в закрытом баллоне, пока его температура не сравняется с температурой 
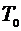в аудитории- состояние (3). Давление газа в этот момент равно:
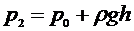, (7)
где h- разность уровней жидкости в манометре.
По измеренным давлениям 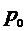, , 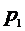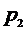можно вычислить отношение теплоемкостей 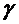. Для этого мысленно выделим внутри баллона произвольную порцию газа, ограниченную замкнутой поверхностью. Эта поверхность на рис. 1 изображена пунктиром. Она играет роль «оболочки», в которую заключена рассматриваемая порция газа постоянной массы. В различных процессах газ, заключенный в эту «оболочку», будет расширяться и сжиматься, совершая работу против давления окружающего газа и обмениваясь с ним теплом. Поскольку кинетическая энергия возникающего макроскопического движения невелика, эти процессы могут рассматриваться как квазистатические. В моменты отсчета давления параметры, характеризующие состояние газа внутри «оболочки», имеют следующие значения:
1 состояние: , ,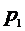 
;
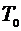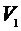2 состояние: 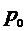, Т,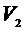 
;
3 состояние: , , .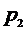
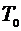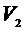Для адиабатического перехода 1- 2 справедливо уравнение Пуассона:
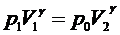. (8)
Состояния 1 и 3 соответствуют комнатной температуре 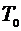, следовательно, к ним можно применить закон Бойля-Мариотта:
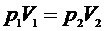. (9)
Из уравнений (8) и (9) можно определить 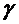. Для этого возведем уравнение (9) в степень 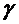и разделим его на уравнение (8):
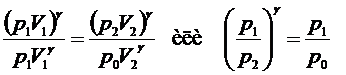. (10)
Логарифмируя (10), получим с учетом (6) и (7):
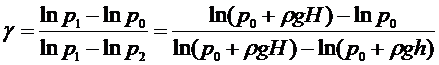. (11)
Так как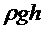 
и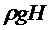 
значительно меньше 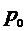, логарифмы можно разложить в ряд, ограничиваясь членами 1-го порядка малости:
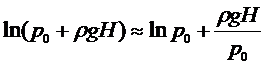(12)
и
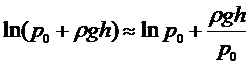. (13)
Подставив выражения (12) и (13) в (11), получим расчетную формулу для :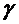
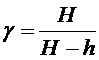. (14)
Следует отметить, что практически невозможно добиться того, чтобы длительность открывания баллона в точности совпала бы со временем адиабатического расширения воздуха. Если перекрыть баллон раньше, чем давление упадет до атмосферного, получим завышенное значение h, обозначим его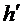 
. Наоборот, при запаздывании получается заниженное значение h, обозначим его 
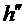, эта величина тем сильнее отличается от h, чем больше время запаздывания 
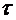. Как показывает опыт, между 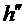, h и 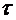выполняется соотношение:
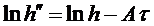, (15)
где А - константа.
На рис. 2. представлен возможный график зависимости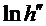 
от различных времен запаздывания 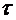, из которого видно, что путем экстраполяции можно найти 
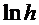и, следовательно, h.
Экспериментальная часть
Описание установки
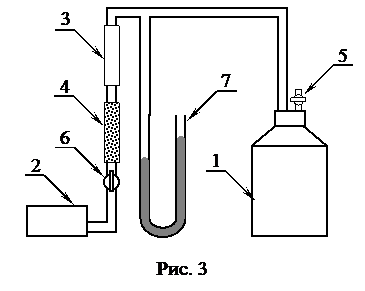Установка для определения 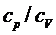изображена на рис. 3. Установка состоит из стеклянного баллона (1), в который накачивается воздух компрессором (2) через ловушку (3)и осушитель (4) до некоторого давления, превышающего атмосферное. Накачивание воздуха в баллон производится при закрытом кране (5) и открытом кране (6). По окончании накачивания кран (6) должен быть закрыт. Разность давлений воздуха в баллоне и окружающей среде измеряется манометром (7).
Выполнение работы
1.
|
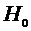=150- 300 мм (точное значение 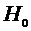задает преподаватель), закрыть кран (6), выключить компрессор. Выждать 2-3 мин, чтобы уровни масла в манометре перестали меняться и сделать отсчет разности уровней Н с точностью до миллиметра. Данные записать в таблицу. 2. Быстро открыть кран (5) и через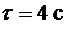 
кран (5) быстро закрыть (время засечь секундомером). Выждав 2-3 мин, пока уровни масла в манометре перестанут меняться, произвести отсчет разности уровней 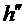с точностью до миллиметра. Данные записать в таблицу.
| № | t, с | H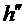, мм | , мм | |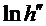
| 1. | ||||
| 2. | ||||
| 3. | ||||
| 4. | ||||
| 5. | ||||
| 6. |
3.Для заданного значения 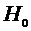повторить опыт для пяти различных времен запаздывания 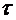(см. таблицу выше) согласно пп. 1-2. Проводя измерения для различных времен запаздывания 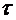, следует строго следить, чтобы начальная разность давлений 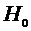была во всех опытах одинакова.
4. Построить график зависимости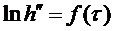 
. Точки должны укладываться на прямую линию (аналогично рис. 2).
5. Определить по графику величину 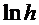. Вычислить среднее значение 
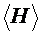, рассчитать погрешность 
.
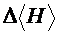6. По формуле (14) вычислить 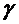. Вычислить абсолютную и относительную погрешности определении 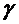. Полученный результат сравнить c теоретическим значением для двухатомного газа, полученным на основе молекулярно-кинетической теории.
Контрольные вопросы
1. Что такое теплоемкость?
2. Как связаны между собой величины 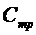и 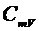? Какая из этих величин больше и почему?
3. В чем заключается метод Клемана-Дезорма? Получите расчетную формулу.
4. Почему при резком открывании крана (5) на короткое время считаем, что газ расширяется адиабатически?
5. Чему равно изменение внутренней энергии газа для любого процесса?
6. Как вычислить молярные теплоемкости и величину 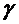через число степеней свободы i молекулы газа?
Литература
1. Сивухин Д.В. Общий курс физики. Термодинамика и молекулярная физика. М.: Наука, 1979.
2. Савельев И.В. Курс общей физики, Т. 1. М.: 1977.
3. Кикоин И.К., Кикоин А. К. Молекулярная физика. М.: 1963.
4. Физические величины: Справочник / Под ред. И. К. Кикоина.- М.: Атомиздат, 1976.
Лабораторная работа № 4