Неравенство Гёльдера в простейшей форме
Рассмотрим график функции 
(см. рисунок):
 | Сосчитаем площади областей, указанных на рисунке. Имеем  . Из уравнения , следует, что  (см. вспомогательные формулы) и поэтому  . Но, как видно из рисунка,  , и поэтому  . |
При выводе этой формулы неявно предполагалось, что 
и 
. Для произвольных а и b это неравенство можно записать в виде
.
Это и есть знаменитое неравенство Гёльдера.
Заметим, что могут быть и другие варианты поведения графика функции и другое соотношение между а и b, но результат всюду будет тот же. Попробуйте сами рассмотреть другие варианты. Кстати, для каких значений параметра р график функции выглядит так, как это изображено на рисунке?
Неравенство Гёльдера для сумм
Пусть даны два набора чисел - 
и 
. Возьмем в неравенстве Гёльдера
и 
.
Тогда неравенство Гёльдера даёт
.
Складывая все эти неравенства, получим
,
откуда получаем
,
что и представляет собой неравенство Гёльдера для сумм.
В случае р = 2 также и q = 2 неравенство Гёльдера принимает вид
.
Неравенство Гёльдера для интегралов
Пусть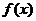 
и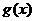 
- две функции, интегрируемые на 
. Возьмем в неравенстве Гёльдера
и 
.
Тогда неравенство Гёльдера даёт
.
Интегрируя это неравенство, получим
откуда получаем
что и представляет собой неравенство Гёльдера для интегралов.
В случае р = 2 также и q = 2 и неравенство Гёльдера принимает вид
.
Это неравенство называется неравенством Буняковского-Коши-Шварца.
Неравенство Минковского
Неравенство Минковского для сумм.
Пусть даны два набора чисел - и . Тогда имеем
Просуммируем эти выражения и к каждой сумме в правой части применим неравенство Гёльдера. Тогда получим
Но (см. вспомогательные формулы)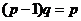 
, и мы получаем
Деля обе части неравенства на 
и учитывая, что 
, получим неравенство
которое и носит название неравенства Минковского.В частном случае р = 2 оно принимает вид
,
которое Вы знаете еще со школы (длина стороны треугольника меньше суммы длин двух других сторон).
Неравенство Минковского для интегралов.
Пусть 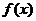и 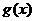- две функции, интегрируемые на . Имеем, аналогично предыдущему,
.
Интегрируя и применяя к каждому интегралу в правой части неравенство Гёльдера для интегралов, получаем
Принимая снова во внимание, что 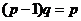будем иметь
Деля на 
и снова учитывая, что учитывая, что , получим неравенство
,
которое также носит название неравенства Минковского.В частном случае р = 2 оно принимает вид
.
Неравенство Иенсена
Это неравенство мы выведем не очень строго.
Пусть
1. 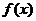есть выпуклая на 
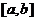функция:
2. 
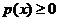и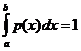 
;
3. 
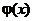непрерывная функция.
Вспомним теперь неравенство Иенсена
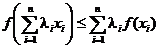
и сделаем в нем следующие замены:
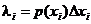, а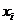 
заменим на 
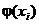. Тогда неравенство Иенсена примет вид
.
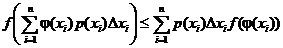Сделаем теперь в этом неравенстве предельный переход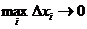 
. Тогда суммы перейдут в интегралы, и мы получим неравенство
.
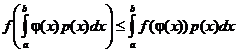Это неравенство и называется неравенством Иенсена в интегральной форме.