Практический признак сходимости.

Пусть 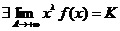, 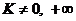. Тогда 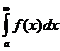сходится при 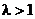и расходится при .

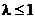(Заметим, что вопрос о том, как же находить l, остается на данном этапе открытым).

Доказательство.

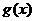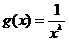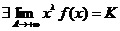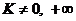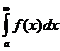Возьмем функцию в виде . Тогда условие теоремы 3 примет вид , и сходится или расходится одновременно с интегралом 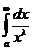.Рассмотрим поэтому вопрос о сходимости этого интеграла.

1. Пусть 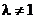. Тогда

.

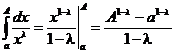Будут два варианта:

а) 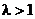. В этом случае 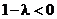, поэтому 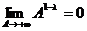и

,

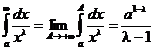так что 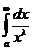сходится.

б) 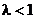. В этом случае 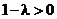, поэтому 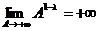и

,

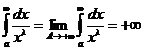так что 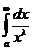расходится.

2. 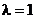. Тогда

,

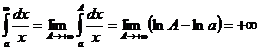так что 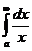расходится.

Таким образом, 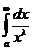сходится при 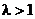и расходится при 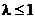. По теореме 2 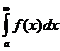также сходится при 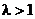и расходится при .<

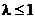Все упирается в нахождение величины l. Как это делать - будет разобрано на практике.

Сходимость несобственных интегралов первого рода от функций произвольного знака.

Рассмотрим теперь признаки сходимости, когда подынтегральная функция 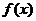может принимать значения любого знака.

Признак Больцано-Коши

Для того, чтобы интеграл 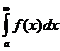сходился необходимо и достаточно, чтобы выполнялось условие

.

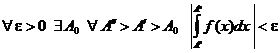Доказательство.

Снова рассмотрим функцию 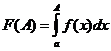. По признаку Больцано-Коши, для существования конечного предела 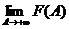необходимо и достаточно выполнение условия

.

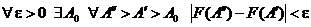Но в нашем случае

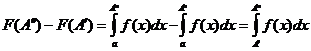
и поэтому признак Больцано-Коши принимает форму, указанную в формулировке теоремы.

Следствие. Если сходится 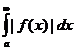, то сходится и .

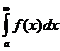Доказательство.

По признаку Больцано-Коши

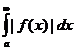сходится Þ .

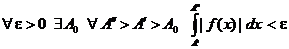(Обратите внимание, что написано так 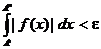, а не так 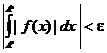; интересно, почему отсутствует знак модуля вокруг интеграла?).

Но тогда 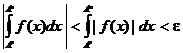и мы получаем, что

,

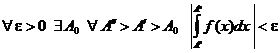откуда, по тому же самому признаку Больцано-Коши следует, что 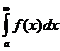сходится. <

Определение.Если 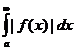сходится, то интеграл 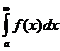называется абсолютно сходящимся (или: интеграл сходится абсолютно). Если же 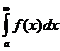сходится, но 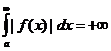, то интеграл 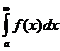называется неабсолютно сходящимся (или: интеграл сходится не абсолютно).

Вообще говоря, a priori не очевидно, что неабсолютно сходящиеся интегралы существуют вообще. Например, оказывается, что когда речь идет о плоскости и так называемых двойных интегралах, неабсолютно сходящихся интегралов не существует, и все двойные интегралы сходятся только абсолютно. Но в одномерном случае такие интегралы существуют, и ниже будет приведен пример такого интеграла.

Признак Больцано-Коши не является «рабочим» признаком, им не проверяется вопрос сходимости какого-то конкретного интеграла. Но на его основе строятся рабочие признаки, два из которых и будут рассмотрены ниже. Но, прежде чем перейти к их изучению, приведем без доказательства одну теорему, которая называется

Вторая теорема о среднем. Пусть

1. функция 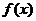интегрируема на отрезке ;

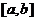2. функция 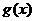монотонна и ограничена на этом отрезке.

Тогда существует точка 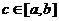, такая, что

.

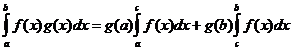Доказывать эту теорему мы не будем.

А теперь перейдем к изучению рабочих признаков сходимости несобственных интегралов.

Признак Дирихле.

Пусть

1. ;

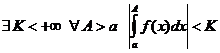2. при 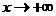функция 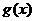монотонно убывает до нуля (запись: ).

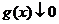Тогда 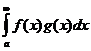сходится.

Доказательство.

1. Из первого ограничения теоремы 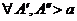имеем

.

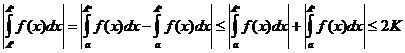2. Из второго ограничения теоремы имеем

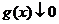Þ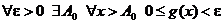

3. Возьмем любые 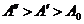. Тогда, используя вторую теорему о среднем, получим

.

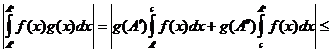
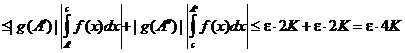Так как e сколь угодно мало, то, по признаку Больцано-Коши, 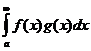сходится.

Следствие.Если 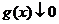, то сходятся следующие интегралы:

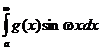(при любых значениях w) и 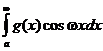(при w ¹ 0)

Доказательство.

Пусть 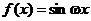или 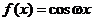. Тогда имеем

,

,

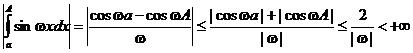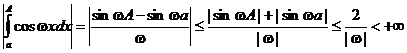если w ¹ 0. Поэтому, по признаку Дирихле, при w ¹ 0 интегралы 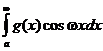и 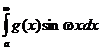сходятся. Последний интеграл сходится и при w = 0 (он просто равен нулю). <

Теперь мы можем рассмотреть

пример неабсолютно сходящегося интеграла.

Таким интегралом является 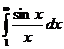. Так как при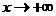 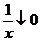, то этот интеграл сходится по признаку Дирихле.

Рассмотрим теперь 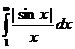. Из достаточно очевидного неравенства

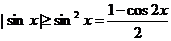
получаем

,

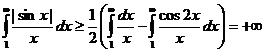так как 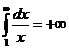(см. практический признак сходимости), а 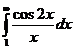сходится по тому же признаку Дирихле. Поэтому 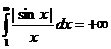и 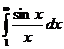сходится неабсолютно.

Признак Абеля.

Пусть

а) функции f (x) и g(x) определены на [a, +¥);

б) интеграл 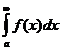сходится (не обязательно абсолютно!);

в) функция g(x) монотонна и ограничена.

Тогда интеграл 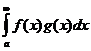сходится.

Доказательство.

Имеем

1. 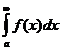сходится Þ ;

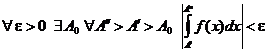2. функция 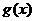ограничена Þ .

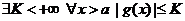3. В силу монотонности функции 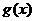можно снова воспользоваться второй теоремой о среднем. Получаем, что для любых любые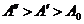

,

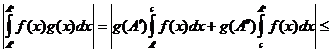
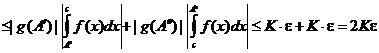и, по признаку Больцано-Коши, 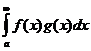сходится. <