Дифференциальная форма закона полного тока

Соотношение (13.3) пригодно для контура любых размеров, в том числе и для весьма малого. Выделим в какой-либо среде небольшой контур («жирно» обведен на рис. 13.3) и составим вдоль него циркуляцию вектора Н. Циркуляция напряженности поля вдоль этого контура равна току, пронизывающему обведенную площадь. Если площадь мала, то можно полагать, что плотность тока d в пределах этой площади одинакова и тогда ток, пронизывающий площадь, Di = dDS = d_nDS. Здесь d_n — проекция вектора плотности тока d на нормаль к площади, т. е. на направление DS; .

За положительное направление нормали к площади принимают направление движения острия правого винта, головка которого вращается в направлении, принятом за поло­жительное при обходе контура и составлении циркуляции.

Рис. 13.3. Иллюстрация к дифференциальному закону полного тока.

Разделим обе части равенства на DS и устремим DS к нулю. Это будет соответствовать стягиванию рассматриваемой площади к нулю. Предел полученного отношения

.

В левой части равенства находится величина, которая является проекцией ротора Н на направление нормали к площади DS. Следовательно, rot_n Н = d_n. Если площадь DS ориентировать в пространстве так, что направление нормали к ней совпадет с направлением вектора плотности тока d в данной точке поля, то тогда вместо равенства проекций двух векторов (rot_nН и d_n) можно записать равенство самих векторов

rot Н = d.(13.4)

Формула (13.4) и представляет собой закон полного тока в дифференциальной форме.

Ротор — это функция, характеризующая поле в рассматриваемой точке в отношении способности к образованию вихрей.

Уравнение (13.4) записано в общей форме, безотносительно к системе координат, и в каждой конкретной системе координат оно раскрывается по-своему.

13.4. Раскрытие выражения rot Н= d в декартовой системе координат

Равенство двух векторов rot Н и dозначает, что равны проекции их на ось х, проекции на ось у и проекции на ось z. Проекция rotН на ось z равна , проекция вектора d на ось z есть d_z и т. д.

На рис. 13.4 в декартовой системе координат изображен малый прямоугольный контур mnpq. Обойдем этот контур против часовой стрелки и составим циркуляцию вектора Н; при ее составлении необходимо учесть изменение вектора Hот точки к точке. Обозначим проекции Н на оси х и у в точке m соответственно через Н_x и H_y.

В точке n проекция на ось x изменится по сравнению с проекцией в точке m и будет равной ; проекцией на ось y будет . В точке q и . В точке p + и .

При составлении циркуляции на участках mn и рq необходимо принимать во внимание лишь «иксовые» составляющие Н( «игрековые» составляющие перпендикулярны элементу пути ).

Составляющую 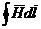на участке mn находят как произведение среднего значения «иксовой» составляющей напряженности на этом участке на длину пути dx

,

на участке np ,

на участке pq ,

на участке qm .

Рис. 13.4. Раскрытие выражения rot H = d в декартовой системе координат.

Если просуммировать все составляющие циркуляции вдоль кон­тура mnpq, то получим:

.

В соответствии с определением проекции ротора на ось z разделим циркуляцию на площадь dS_z = dxdy, после чего проекция ротора на направление оси z:

.

Аналогично,

и .

Таким образом,

.(13.5)