Применение I начала термодинамики к изопроцессам
Среди равновесных процессов, происходящих в термодинамических системах (газах), выделяют изопроцессы, при которых один из параметров состояния остается постоянным.
Изохорный процесс (V = const). В координатах P, V изохорный процесс изображается прямой параллельной оси ординат (рис. 6.3, а). В изохорном процессе газ не совершает работы, т. е. 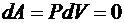 . Тогда из первого начала термодинамики количество теплоты выражается зависимостью вида:
. Тогда из первого начала термодинамики количество теплоты выражается зависимостью вида:
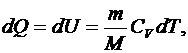
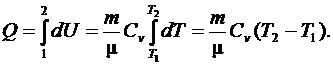 (6.21)
(6.21)
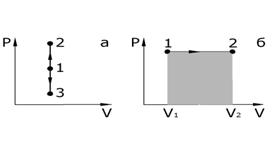 | Таким образом, в изохорном процессе все тепло, сообщенное газу, идет на увеличение его внутренней энергии. |
| Рис. 6.3 |
Изобарный процесс (P = const). Диаграмма этого процесса (изобара) изображается прямой параллельной оси x. Работа при расширении газа от V1 до V2 определяется как
 (6.22)
(6.22)
Работа численно равна площади заштрихованного прямоугольника на рис. 6.3, б. Если воспользоваться уравнением Менделеева – Клапейрона ( 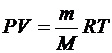 ), откуда следует, что
), откуда следует, что 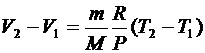 , то выражение (6.22) примет вид
, то выражение (6.22) примет вид
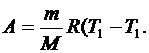 (6.23)
(6.23)
С учетом выражений параграфа 6.4 первое начало термодинамики для изобарного процесса в дифференциальной форме можно представить в виде
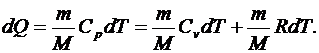 (6.24)
(6.24)
Изотермический процесс (T = const). Уравнением изотермического процесса является закон Бойля-Мариотта
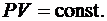 (6.25)
(6.25)
Диаграмма изотермического процесса приведена на рис.6.4.
Работа в изотермическом процессе (T = const) может быть определена как
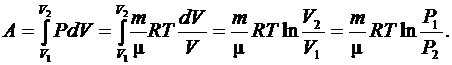 (6.26)
(6.26)
 Рис. 6.4 Рис. 6.4 | Согласно первому началу термодинамики 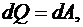 так как так как 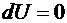 при при 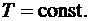 В изотермическом процессе все количество теплоты, сообщаемое газу, расходуется им на совершение работы против внешних сил В изотермическом процессе все количество теплоты, сообщаемое газу, расходуется им на совершение работы против внешних сил |
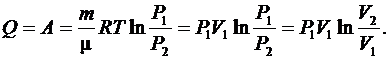 (6.27)
(6.27)
Теплоемкость изотермического процесса стремится к бесконечности, т. е.
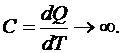 (6.28)
(6.28)
Адиабатический процесс
Адиабатическим называется процесс, при котором отсутствует теплообмен между термодинамической системой и окружающей средой 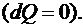
Из первого начала следует, что
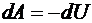 (6.29)
(6.29)
или
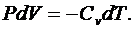 (6.30)
(6.30)
Найдем уравнение, связывающее параметры состояния в адиабатном процессе. Для этого продифференцируем уравнение состояния для 1 моля газа
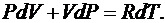 (6.31)
(6.31)
Разделив уравнение (6.31) на выражение (6.30), получим
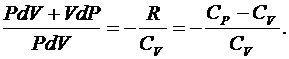 (6.32)
(6.32)
Разделим переменные, тогда с учётом 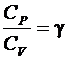 выражение (6.32) примет вид
выражение (6.32) примет вид
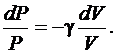 (6.33)
(6.33)
Интегрируя (6.32) в пределах от Р1 до Р2 и от V1 до V2, получим
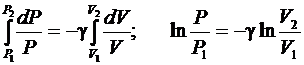 ; (6.34)
; (6.34)
или
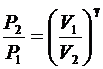 или
или 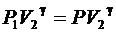 (6.35)
(6.35)
Так как состояния 1 и 2 выбраны произвольно, то (6.35) можно записать:
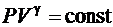 (6.36)
(6.36)
Уравнение (6.36) называется уравнением Пуассона, которое описывает адиабатический процесс. Используя уравнения Клапейрона – Менделеева, можно записать уравнение Пуассона в виде
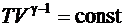 (6.37)
(6.37)
или
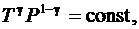 (6.38)
(6.38)
где g – коэффициент Пуассона, равный 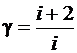 ; при i = 3g = 1,67, при i = 5, g = 1,4.
; при i = 3g = 1,67, при i = 5, g = 1,4.
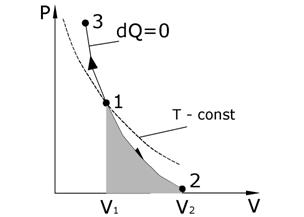
График адиабаты представлен на рис. 6.5. Адиабата более крута, чем изотерма. Это объясняется тем, что увеличение давления газа обусловлено не только уменьшением объема как при изотермическом сжатии, но и повышением температуры. При адиабатическом процессе изменяются все три параметра P, V и T .
 | Вычислим работу, совершаемую газом при адиабатическом процессе: 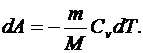 (6.39) Интегрируя выражение (6.39), получим (6.39) Интегрируя выражение (6.39), получим |
| Рис.6.5 |
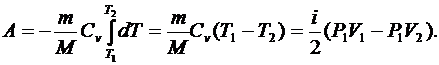 (6.40)
(6.40)
Работа, совершаемая газом при адиабатическом процессе, численно равная заштрихованной площади на рис. 6.5, меньше, чем при изотермическом процессе.
Политропный процесс
Все рассмотренные выше процессы обладают одной общей особенностью – они происходят при постоянной теплоемкости С
при 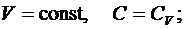
при 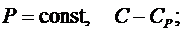 (6.41)
(6.41)
при 
при 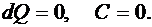
Процессы, в которых теплоемкость постоянна, называют политропными. Все изопроцессы, включая адиабатический, являются частными случаями политропного процесса.
Аналогично выводу уравнения адиабаты (6.37), используя первое начало термодинамики и уравнение Менделеева – Клапейрона для 1 моля,

получим
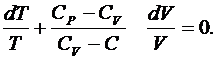 (6.42)
(6.42)
Интегрируя выражение (6.42), получим уравнение политропы
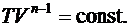 (6.43)
(6.43)
Заменив в (6.43) температуру T соотношением, полученным из уравнения Менделеева – Клапейрона, как 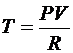 , получим
, получим
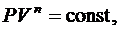 (6.44)
(6.44)
где 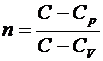 – показатель политропы.
– показатель политропы.
При 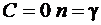 получим
получим 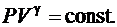
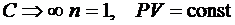 – уравнение изотермы;
– уравнение изотермы;
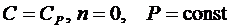 – уравнение изобары; (6.45)
– уравнение изобары; (6.45)
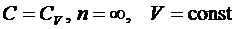 – уравнение изохоры.
– уравнение изохоры.
