Вычислить кинетическую энергию электрона, находящегося на второй орбите атома водорода.

67. Определить число атомов, распадающихся в 1 г радия ²²⁶Ra₈₈ за 1 с, если его период полураспада - 1600 лет.

68. Определить длину волны де Бройля для протона, движущегося со скоростью υ=0,6 м/с.

69. Найти массу радона ²²Rn₈₆ , активность которого равна 2 Кu. Период полураспада радона Т_1/2 = 3,8 дня.

70. Определить дефект массы и энергию связи ядра атома лития ⁷Li₃ (m(⁷Li₃) = 7,01601 а.е.м., m_n = 1,00867 а.е.м., m(¹Н₁)= 1,00783 а.е.м.,).

71. На сколько процентов должна уменьшиться в 2006 году активность стронция ⁹⁰Sr₃₈ (T_1/2 = 28 лет), выпавшего в 1986 году во время Чернобыльской аварии?

72. Для биологического исследования кролику с пищей введён радиоактивный натрий ⁴²Na₁₁ , активность которого А = 0,1 мкКи. Определить массу введённого радиоактивного элемента. Период полураспада ⁴²Na₁₁ равен 16,96 часа.

73. Некоторый радиоактивный препарат имеет постоянную распада λ = 1,44 • 10^-3 r^-1. Через сколько времени распадётся 75% первоначального количества атомов?

74. Какой изотоп образуется из ²³⁸U₉₂ после двух β — распадов и одного

α - распада? Написать реакцию.

75. Радиоактивный висмут ²¹³Bi₈₂ распадается, излучая β - частицы. Период полураспада Т_1/2= 46минут. Определить число атомов, распавшихся в 0,1 г висмута за 1 час.

76. Для сиробиологических исследований в питательную смесь введён 1 мг радиоактивного изотопа ³²Р₁₅, период полураспада которого 14.28 суток. Определить постоянную распада и активность фосфора.

77. Найти длину волны де Бройля для электрона, движущегося со скоростью υ = 2 • 10³ м/с.

Счётчик Гейгера вблизи радиоактивного вещества отсчитал в 1 минуту 480 распадов, а спустя 2 часа - 150 распадов в минуту. Определить период полураспада.

79. Определить энергию связи ядра атома азота ¹⁴N₇ (m (¹⁴N₇) = 14,00307 а.е.м., m(¹H₁)=l,00783 а.е.м., m„=1,00867 а.е.м.).

80. Определить энергию ядерной реакции ⁴Не₂ + ¹⁰В₅ → ¹Н₁ + ^l3C₆ (m(4Не2) = 4,00260 а.е.м., m(^l3C₆) = 13,00335 а.е.м., m(¹⁰В₅) = 10,01294 а.е.м. m(¹Н₁) = 1.00783 а.е.м.).

81. При радиоактивном распаде из ядра ²³⁸U₉₂ испускается три

α-частицы. В ядро какого элемента превращается в процессе распада ядро атома урана?

82. Определить дефект массы и энергию связи ядра трития ³Н₁ (m(³H₁) = 3,01605 а.е.м., m(¹n₀) = 1.00867 а.е.м., m(¹Н₁) = 1,00783 а.е.м).

83. Вычислить энергию ядерной реакции ²Li₃ + ²H₁ → 2 ⁴Не₂ + ¹n₀ (²Li₃) = 7.01601 а.е.м., m(²Н₁) = 2,01410 а.е.м., m(⁴Не₂) = 4.00260 а.е.м., m(¹n₀)= 1.00867 а.е.м.).

Чему равна длина волны де Бройля теплового нейтрона, обладающего энергией, равной средней энергии теплового движения при температуре 300 К?

85. Найти энергию связи атома бора ¹¹В₅ (m(¹¹B₅) = 11,00930 а.е.м., m(¹Н₁) = 1.00783 а.е.м., m_n = 1,00867 а.е.м.).

86. Найти среднюю продолжительность жизни атома радиоактивного изотопа ⁶⁰Со₂₇(Т_1/2 = 5,26 лет).

87. Вычислить энергию ядерной реакции ⁹Ве₄ + ⁴Не₂ → ¹²С₆ + ¹n₀ (m_n = 1.00867 а.е.м., m(⁹Ве₄) = 9,01219 а.е.м., m(⁴Не₂) = 4,00260 а.е.м., m(¹²С₆) =12.00000 а.е.м.).

88. Найти энергию связи, приходящуюся на один нуклон, ядра урана ²³⁸U₉₂ (m(²³⁸U₉₂)=238,05077 а.е.м., m(¹Н₁) = 1,00783 а.е.м., m_n = 1.00867 а.е.м.).

89. Вычислить энергию ядерной реакции ³H₁ + ¹H₁ → ³He₂ + ¹n₀(m_n 1.00867 а.е.м., m(¹H₁) = 1,00783 а.е.м., m(³H₁) = 3,01605 а.е.м., m(³He₂) = =3.01603 а.е.м.).

Определить энергию, массу и импульс фотона с энергией 1МэВ.

На какой уровень переходит с четвёртого уровня электрон, если энергия излученного атомом водорода фотона равна 2,55 эВ.

92. Найти энергию ядерной реакции ^l4N₇ + ⁴Не₂ → ¹Н₁ + ¹⁷O₈

(m(^l4N₇)=l4.00307 а.е.м., m(¹H₁) - 1,00783 а.е.м., m(⁴Не₂) = 4,00260 а.е.м., m(¹⁷O₈) = 16,99913 а.е.м.).

93. Определить длину волны де Бройля λ, характеризующую волновые свойа электрона, если его скорость и равна 1000 км/с.

94. Сколько атомов распадается за 30 суток из миллиарда атомов радия, если его период полураспада Т_1/2 = 1600 лет?

95. Вычислить энергию ядерной реакции ¹⁶O₈ + ²Н₁ → ¹⁴N₇ +⁴Не₂ (m(⁴He₂) = 4,00260 а.е.м., m (²Н₁)= 2,01410 а.е.м., m(^l4N₇) = 14.00307 а.е.м., m(¹⁶O₈)= 15,99492 а.е.м.).

96. Какой изотоп образуется из радиоактивного изотопа ⁸Li₃ после одного β - распада и одного α - распада?

Вычислить энергию, которую поглощает атом водорода при переходе электрона со второго энергетического уровня на пятый.

Найти наибольшую длину волны в ультрафиолетовой серии Лаймана спектра водорода.

99. Какой изотоп образуется из 234U92 после двух β - распадов и одного

α -распада?

100. Какой изотоп образуется из урана ²³⁸U₉₂ после трёх α - распадов и двух β - распадов? Написать реакцию.

Примерный билет к модулю №2 по теме:

«Строение атома. Радиоактивность»

Строение атома. Опыт Резерфорда.

Уравнение Шредингера.

Линейный размер атомного ядра.

Единица активности радиоактивного излучения. Чему она равна?

Методы наблюдения и регистрации микрочастиц (перечислить). Сцинтилляционный счетчик.

Определить длину волны света, при которой возможна ионизация атома водорода, находящегося в основном состоянии.

7. Определить число атомов , распадающихся в 1 г радия ²²⁶Ra₈₈ за 1 с, если его перод полураспада Т_1/2 = 1600 лет.

Счетчик Гейгера вблизи радиоактивного вещества отсчитал в 1 минуту 480 распадов , а спустя 2 часа – 150 распадов в минуту. Определить период полураспада.

9. Вычислить энергию ядерной реакции ³Н₁ + ¹Н₁ → ³Нег + ¹n₀ (m_n = 1.00867 а.е.м., m(¹H₁) = 1,00783 а.е.м., m(³Н₁) = 3,01605 а.е.м., m(³He₂) = 3.01603 а.е.м.).

10. какой изотоп образуется из ²³⁹U₉₂ после трех α – распадов и двух β - распадов? Написать реакцию.

Задания

Для расчетно-графических работ.

Задача 1

В опыте Юнга две щели S₁ и S₂ находятся на расстоянии d и освещаются монохроматическим светом с длиной волны λ. Интерференционная картина наблюдается на экране, отстоящем от щелей на расстоянии L (рис 1). В точке О наблюдается нулевой максимум. На расстоянии y от его середины наблюдается максимум с номером К, а на расстоянии Z наблюдается минимум с номером m. Ширина интерференционной полосы равна X. Числовые данные приведены в таблице. Определить величины, обозначенные в таблице вопросительным знаком.

вариант	d, мм	λ, кмм	L, м	y, см	К	Z, см	m	X, мм
	?	0,6						?
		?		1,12				?
		0,5		?				?
		0,7		?				?
		0,6		1,2	?			?
		0,7				?		?
		0,7				1,33	?	?
	?	0,6	1,5	?
		?				?		1,4
		0,7	?		?

Задача 2

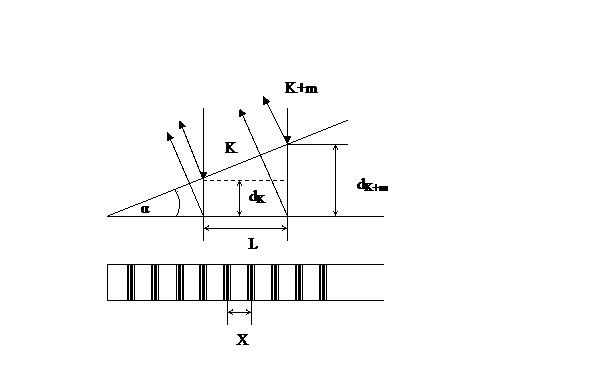
На клин с малым преломляющим углом α и показателем преломления n нормально к его грани падает свет с длиною волны λ (см.рис.). Вследствие интерференции света на поверхности наблюдаются светлые и темные полосы, параллельные ребру клина. Ширина интерференционной полосы равна X. Расстояние между темными полосами K и K+m равно L. Числовые данные приведены в таблице. Определить величину, обозначенную в таблице знаком вопроса.

вариант	λ, мкм	α , рад	n	K	K+m	L, см	X, мм
	0,5	10-4	1,3	?		1,9
	0,5	10-4	1,3		?	3,8
	0,4	5·10-5	1,3			?
	0,56	2·10-4	1,4				?
	?	2·10-4	1,4
	0,52	?	1,3
	0,6	2·10-4	?
8	?	2·10-4	1,5
	0,6	?	1,5
	0,6	10-4	?

Задача №3

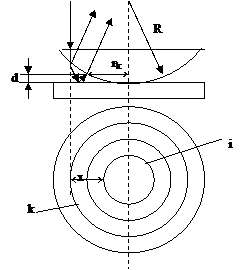
Плоско-выпуклая линза лежит на стеклянной пластине. Радиус кривизны равен R. Показатель преломления вещества, находящегося в зазоре между линзой и пластиной, равен n. На систему линза-пластина нормально падает свет с длиной волны λ. Радиус темного кольца с номером k равен r_{k ,} с номером i - r_i. Расстояние между темными кольцами с номерами k и i равно x. Значения величин указаны в таблице. Определить значение величины, обозначенной в таблице вопросительным знаком. В центре колец наблюдается темное пятно. Толщина клина, соответствующая k-му темному кольцу, равна d_k.

вариант	λ, мкм	R, м	k	i	rk, мм	ri,мм	dk, мм	n	x,мм
	0,6						?
	0,6				?			1,3	1,3
	0,64								?
	0,5	?
	0,5	?
	0,64		?		3,2
	0,7							?
	0,64	?			0,4			1,3
	?							1,3
	0,6	0,6		?		0,6

Задача 4

На прямоугольную щель шириной b падает нормально к ней параллельный пучок монохроматического света с длиной волны λ. На экране, отстоящем от щели на расстоянии L , наблюдается дифракционная картина. Ширина нулевого максимума равна x . Максимум с номером k наблюдается под углом φ_k к первоначальному направлению. Расстояние между минимумами с номерами m и n равно y. Значения величин приведены в таблице. Определить значение величины, указанной в таблице вопросительным знаком.

Вариант	b, мм	λ, мкм	L, м	x, мм	k	φk, град	m	n	y,мм
	0,05	?	0,5
	0,2	0,7	?
	0,1	0,5	1,5	?
	?	0,6				0,5
	0,1	0,6		?					?
	0,1	?		?
	0,1	0,55					?
	0,1	0,5	?
	0,1	0,5	?
	0,2	0,6		?		?

Задача 5

На дифракционную решетку нормально ее поверхности падает параллельный пучок света с длиной волны λ. Линза проецирует дифракционную картину на экран, удаленный от линзы на расстояние L (смотри рисунок). Расстояние между максимумами с номерами 0 и k равно x, а между максимумами первого порядка y. Угол дифракции, соответствующий максимуму наибольшего порядка k_max равен φ_max. Число всех максимумов наблюдаемых на экране равно n. Решетка имеет длину ℓ и содержит N щелей. Определить величину, обозначенную в таблице вопросительным знаком.

Вариант	N	ℓ, см	λ, мкм	L,м	k	x, см	y, см	kmax	φmax	n
			?
			0,5	?
			0,15		?
			0,5			?
			0,5				?
			0,6					?
		1,2	0,55						?
			0,7							?
		?	0,6
	?		0,7

Задача 6

Два поляроида расположены так, что их главные направления P₁P₁ и P₂P₂ составляют угол φ (см.рис.). Коэффициент поглощения света в первом поляроиде равен k₁, во втором – k₂. На первый поляроид падает свет, интенсивность которого равна I₀. Интенсивность света прошедшего через первый поляроид, равна I₁ , а через второй – I₂. На первый поляроид падает естественный свет (случай 1).

На первый поляроид падает плоскополяризованный свет, плоскость колебаний которого составляет угол α с главным направлением P₁P₁ первого поляроида (случай 2).