Плотной среды. Подставляя в формулу значение разности хода, получим

,

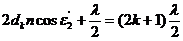Где n – коэффициент стекла (n = 1,5); d_k толщина клина в том месте, где наблюдается темная полоса, соответствующая номеру k.

Согласно условию, угол падения равен нулю, следовательно, и угол преломления ε'₂ равен нулю, a cosε'₂ = 1. Раскрыв скобки в правой части равенства, после упрощения получим

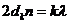
Пусть произвольной темной полосе номера k соответствует определенная толщина клина в этом месте d_k, а темной полосе номера k+10 соответствует толщина d_k+10. Согласно условию задачи, 10 полос укладываются на отрезке длинной 1 см. Тогда искомый угол будет равен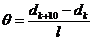

Где из-за малости преломляющегося угла sinθ ≈ θ.

Вычислив d_k и d_k+10, подставив их в формулу и произведя преобразования, найдем

.

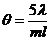После вычисления получим θ = 2 · 10^-4 рад или 41,2``.

Ответ: θ = 41,2``.

Задачи.

1. От двух когерентных источников S₁ и S₂ (λ = 0,8 мкм) лучи попадают на экран. На экране наблюдается интерференционная картина. Когда на пути одного из лучей перпендикулярно ему поместили мыльную плёнку (n =1,33), интерференционная картина изменилась на противоположную. При какой наименьшей толщине d_min плёнки это возможно?

2. На стеклянный клин с малым углом нормально к его грани падает параллельный пучок лучей монохроматического света с длиной волны λ= 0,6 мкм. Число m возникающих при этом интерференционных полос, приходящихся на l см, равно 10. Определить угол α клина.

3. На пути пучка света поставлена стеклянная пластина толщиной d = 1 мм так, что угол падения луча i₁ =30⁰. Насколько изменится оптическая длина пути светового пучка?

4. На мыльную плёнку с показателем преломления n = 1.33 падает по нормали монохроматический свет с длиной волны λ= 0,6 мкм. Отражён-ный свет в результате интерференции имеет наибольшую яркость. Какова наименьшая возможная толщина d_min плёнки?

5. Радиус второго тёмного кольца Ньютона в отражённом свете r₂= 0,4 мм. Определить радиус R кривизны плосковыпуклой линзы, взятой для опыта, если она освещается монохроматическим светом с длиной волны λ= 0,64 мкм.

6. Между стеклянной пластинкой и лежащей на ней плосковыпуклой линзой находится жидкость. Найти показатель преломления жидкости, если радиус r₃ третьего тёмного кольца Ньютона при наблюдении в отраженном свете с длиной волны λ= 0,6 мкм равен 0,82 мм. Радиус кривизны линзы R = 0,5 м.

7. На тонкую плёнку в направлении нормали к её поверхности падает монохроматический свет с длиной волны λ= 500 нм. Отраженный от неё свет максимально усилен вследствие интерференции. Определить мини-мальную толщину d_min плёнки, если показатель преломления материала плёнки n =1,4.

8. Расстояние L от щелей до экрана в опыте Юнга равно 1м. Определить расстояние между щелями, если на отрезке длиной l = 1 см укладывается N = 10 тёмных интерференционных полос. Длина волны λ= 0,7 мкм.

9. На стеклянную пластину положена выпуклой стороной плосковыпук-лая линза. Сверху линза освещена монохроматическим светом с длиной волны λ= 500 нм. Найти радиус R линзы, если радиус четвертого кольца Ньютона в отражённом свете r₄ = 2 мм.

10. На тонкую глицериновую плёнку толщиной d = 1,5 мкм нормально к её поверхности падает белый свет. Определить длины волн λ лучей видимого участка спектра (0,4 ≤ λ ≤ 0,8 мкм), которые будут ослаблены в результате интерференции.

11. На стеклянную пластинку нанесён тонкий слой прозрачного вещест-ва с показателем преломления n = 1,3. Пластинка освещена парал-лельным пучком монохроматическим светом с длиной волны λ= 640 нм, падающим на пластинку нормально. Какую минимальную толщину d_min должен иметь слой, чтобы отражённый пучок имел наименьшую яркость?

12. На тонкий стеклянный клин падает нормально параллельный пучок света с длиной волны λ= 500 нм. Расстояние между соседними темными интерференционными полосами в отражённом свете b = 0,5 мм. Опре-делить угол α между поверхностями клина. Показатель преломления стекла, из которого изготовлен клин, n =1,6.

13. Плосковыпуклая линза с фокусным расстоянием f = 1 м лежит выпуклой стороной на стеклянной пластинке. Радиус пятого тёмного кольца Ньютона в отражённом свете r₅ = 1,1 мм. Определить длину световой волны λ.

14. Два когерентных источника испускают монохроматический свет с длиной волны λ= 600 нм. Определить на каком расстоянии от центра экрана будет расположен первый максимум интерференционной карти-ны, если расстояние между источниками 1 мм, а расстояние от плоскости экрана до плоскости , в которой расположены когерентные источники равно 4 м?

Два когерентных источника света посылают на экран свет длиной волны 550 нм, дающий на экране интерференционную картину. Источники тока удалены один от другого на 2,2 мм, а расстояние от экрана равно 2,2 м. Определить, что будет наблюдаться на экране в точке, находящейся под каждым источником.