Сборник задач по курсу физики
Л.В.Гулин, С.В.Анахов
СБОРНИК ЗАДАЧ ПО КУРСУ ФИЗИКИ
Учебно-методическое пособие
Екатеринбург
ББК В3я73
УДК 530.1 (076)
Г 94
Сборник задач по курсу физики: Учеб.-метод. пособие / Л.В.Гулин, С.В.Анахов. -Екатеринбург: ГОУ ВПО «Российский гос. проф.-пед.ун-т», 2009. – 120 с.
В учебно-методическом пособии приведены варианты контрольных работ по курсу физики, даны методические указания к их выполнению, примеры решения типовых задач.
Предназначено студентам инженерно-педагогических и профессионально-педагогических специальностей.
Отв. редактор доктор физико-математических наук, профессор А.С. Борухович
Рецензенты: заведующий кафедрой общей физики Уральского государственного педагогического университета доктор физико-математических наук, профессор П.С. Попель; заведующий кафедрой микропроцессорной техники Российского государственного профессионально-педагогического университета кандидат технических наук, доцент А.А. Карпов
| У У | Гулин Л.В., Анахов С.В., 2009 ГОУ ВПО «Российский государственный профессионально-педагогический университет», 2009 |
Введение
В условиях интенсивного научно-технического прогресса необходимо повышение уровня естественнонаучного образования. Для этого максимальное внимание должно быть уделено изучению в высших учебных заведениях любого профиля дисциплин, составляющих фундамент современного учения об окружающем мире.
В этом смысле физика занимает особое положение. Именно на ее основе развиваются все направления техники. В недрах физики появились многие основополагающие идеи современной химии и биологии. На стыке физики и математики родилась кибернетика. Достижения физики последних десятилетий стимулировали появление новой междисциплинарной науки - синергетики. Изучение физики расширяет общий кругозор, развивает критический подход к анализу не только явлений живой и неживой природы, но и закономерностей развития общества.
Современная физика как наука является важнейшим достижением общечеловеческой культуры в целом. Постоянное оперирование моделями при изучении физики вырабатывает способность к абстрактному мышлению, выделению в том или ином явлении главного, а широкое применение математического аппарата приучает к использованию научных методов. Современный специалист любого профиля встречается в своей практике с большим числом разнообразных механизмов, приборов и методов исследования. Понять принципы действия большинства из них невозможно без общефизической подготовки.
Настоящий сборник задач поможет студентам овладеть приемами и методами решения конкретных задач из различных областей физики.
ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ
1.1. Самостоятельная работа студента
Учебная работа студента по курсу физики складывается из работы на установочных лекциях и практических занятиях во время лабораторно-экзаменационной сессии и решения задач контрольной работы в ходе самостоятельного изучения курса в межсессионный период.
Самостоятельное изучение курса физики следует проводить по учебным пособиям и учебникам [1-12]. Справочные материалы, необходимые при решении задач, приведены в приложении.
Сдача экзамена и зачета
Изучение физики в каждом семестре заканчивается сдачей экзамена или зачета. Вид отчетности определяется учебным планом и зависит от специализации, формы и сроков обучения.
Необходимое условие допуска студента к сдаче экзамена или зачета - выполнение всех контрольных мероприятий и лабораторных работ. Для студентов-заочников обязательным является собеседование с преподавателем, проверяющим контрольную работу. Только при положительном результате собеседования студент получает зачет по контрольной работе и допускается к сдаче семестрового экзамена или зачета.
Экзамены и зачеты проводятся по расписанию во время лабораторно-экзаменационной сессии. По нормам высшей школы на экзамен выделяется целый день, на зачет - половина рабочего дня.
Экзамены принимаются по билетам или тестам, утвержденным заведующим кафедрой. В билете, как правило, имеется два теоретических вопроса и задача. Перечень теоретических вопросов комплекта билетов сообщается или выдается студентам на установочной сессии. Студенты, показавшие отличные и хорошие знания при защите контрольных работ, освобождаются от решения задачи на экзамене. Студенты, отлично выполнившие контрольные работы, по представлению преподавателя могут быть освобождены заведующим кафедрой от экзамена с проставлением в экзаменационную ведомость оценки "отлично". Список таких студентов сообщается учебной группе перед началом экзамена или зачета.
Зачет может приниматься по усмотрению преподавателя по билетам, тестам или по результатам выполнения контрольной работы.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Механика (№№ 101-170)
Пример 1. Эскалатор поднимает идущего по нему вверх человека за t1=1 мин. Если человек будет идти вдвое быстрее, то он поднимется за t2=45 с. Сколько времени будет подниматься человек, стоящий на эскалаторе?
Решение. Пусть искомое время равно  t; расстояние, которое человек проезжает на эскалаторе, равно s, а скорость движения эскалатора равна v. При равномерном движении эти величины связаны соотношением
t; расстояние, которое человек проезжает на эскалаторе, равно s, а скорость движения эскалатора равна v. При равномерном движении эти величины связаны соотношением
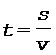 . (1)
. (1)
Аналогичные соотношения могут быть записаны для t1 и t2:
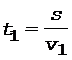 , (2)
, (2)
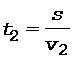 . (3)
. (3)
Скорости v1 и v2 можно найти следующим образом:
v1 = v + vо, (4)
v2 = v + 2vо, (5)
где v0 - скорость движения человека относительно эскалатора в случае, когда время подъема равно t1.
Подставляя соотношения (4) и (5) в формулы (2) и (3), получим
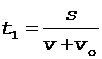 , (6)
, (6)
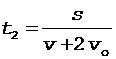 . (7)
. (7)
Перепишем соотношения (6) и (7) в виде
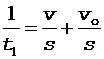 ,
,
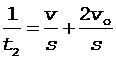 .
.
Введем обозначение x = vо/s. Тогда с учетом соотношения (1) получим систему уравнений
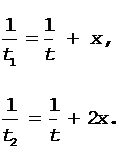


Почленное вычитание уравнения (8) из уравнения (9) дает
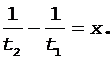
Подставляя x в уравнение (8), получим
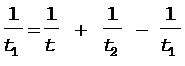 .
.
После преобразований получим выражение
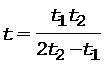 .
.
Выразив t1 в секундах, находим
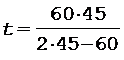 = 90 с.
= 90 с.
Пример 2. Скорость тела, движущегося прямолинейно, меняется по закону v = At + Bt3, где A = 1 м/с2; B = 3 м/с4.
Чему будет равно ускорение тела к моменту времени, когда оно пройдет расстояние s = 14 м?
Решение. Ускорение есть производная от скорости по времени:
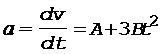 . (1)
. (1)
Время t находим, используя соотношение
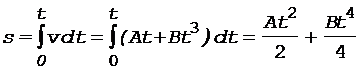 . (2)
. (2)
Введем обозначение z = t2 и, используя исходные данные, запишем соотношение (2) в виде
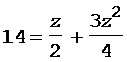 .
.
После преобразований получим уравнение
3z2 + 2z - 56 = 0. (3)
Решение уравнения (3) дает
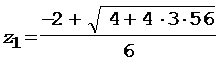 = 4 с2,
= 4 с2,
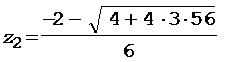 = -4,7 с2.
= -4,7 с2.
Значение z2 должно быть отброшено, так как в соответствии с введенным обозначением z > 0. Подставляя z = 4 с2 в уравнение (1), находим
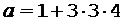 = 37 м/с2.
= 37 м/с2.
Пример 3. Траектория движения материальной точки задается уравнениями: x = At2; y = Bt, где A = 4 м/с2; B = 2 м/с. Радиус кривизны траектории через промежуток времени t = 1 с после начала движения равен R = 17 м. Определить полное ускорение точки в этот момент времени. Построить траекторию движения за первые две секунды.
Решение. Уравнение траектории задано в параметрическом виде:
x = At2, (1)
y = Bt. (2)
Чтобы получить уравнение траектории в явном виде, исключим время из уравнений (1) и (2):
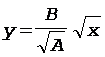 .
.
Полученное выражение представляет собой уравнение верхней ветви параболы, ось которой направлена вдоль оси x. Для построения траектории найдем по уравнениям (1) и (2) значения x и y в моменты времени, взятые с интервалом 0,5 с:
| t, c | x, м | y,м |
| 0,0 | ||
| 0,5 | ||
| 1,0 | ||
| 1,5 | ||
| 2,0 |
Траектория движения точки представлена на рис. 1.
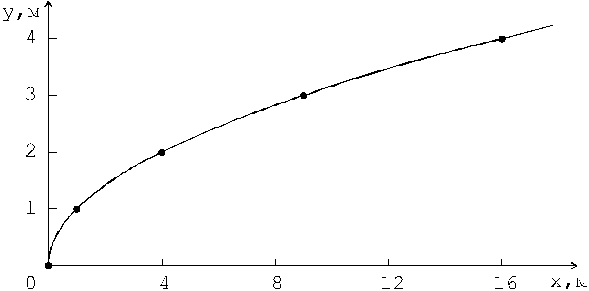 |
Рис. 1
Полное ускорение определяется по формуле
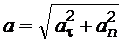 , (3)
, (3)
где 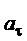 и
и 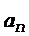 - тангенциальное и нормальное ускорения соответственно. Эти ускорения находим по формулам
- тангенциальное и нормальное ускорения соответственно. Эти ускорения находим по формулам
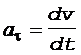 , (4)
, (4)
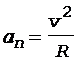 , (5)
, (5)
где v - модуль вектора скорости точки, определяемый по формуле
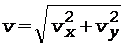 . (6)
. (6)
В свою очередь, vx и vy - проекции вектора скорости на оси x и y - вычисляются по формулам
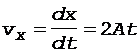 , (7)
, (7)
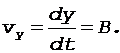 (8)
(8)
Подставляя уравнения (7) и (8) в (6), получим
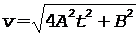 , (9)
, (9)
а затем в соответствии с формулой (4) находим
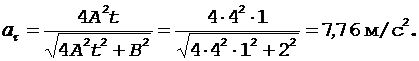 (10)
(10)
Вычисления по формуле (9) дают значение модуля скорости, равное v = 8,25 м/с, что после подстановки в уравнение (5) позволяет определить нормальное ускорение:
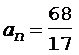 = 4 м/с2. (11)
= 4 м/с2. (11)
Подставляя результаты вычислений по формулам (10) и (11) в выражение (4), находим полное ускорение:
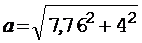 = 8,73 м/с2.
= 8,73 м/с2.
Пример 4. Шайба лежит на платформе, вращающейся вокруг вертикальной оси. Расстояние от шайбы до оси вращения равно R = 2 м. При частоте вращения n = 9 об/мин шайба начинает скользить по платформе. Определить коэффициент трения шайбы о платформу.
Решение. На шайбу действуют три силы (рис. 2): сила тяжести 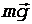 , сила нормальной реакции опоры
, сила нормальной реакции опоры 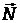 и сила трения
и сила трения 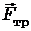 .
.
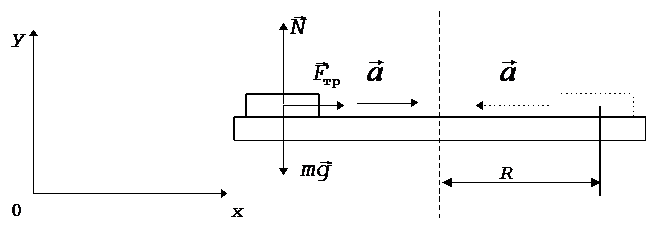
Рис.2
Запишем уравнение движения шайбы (второй закон Ньютона) сначала в векторной форме:
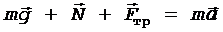 ,
,
затем в проекциях на оси Ox:
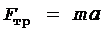 (1)
(1)
и Oy:
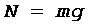 . (2)
. (2)
Оставаясь неподвижной относительно платформы, шайба вместе с тем движется с ускорением, которое является центростремительным и определяется по формуле
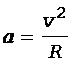 , (3)
, (3)
где v - линейная скорость шайбы.
Модуль силы трения вычисляется по формуле
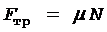 , (4)
, (4)
где m - коэффициент трения.
Перепишем формулу (4) с учетом уравнения (2):
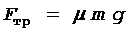 , (5)
, (5)
а уравнение (1) - с учетом формул (3) и (5):
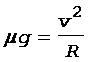 . (6)
. (6)
Линейная скорость связана с частотой вращения соотношением
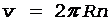 . (7)
. (7)
Подставляя уравнение (7) в формулу (6), имеем
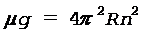 .
.
После преобразований и подстановки исходных данных в системе СИ получим
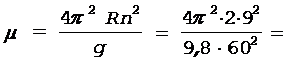 0,18.
0,18.
Пример 5. Конькобежец массой m1, стоя на льду, толкает в горизонтальном направлении камень массой m2 = 5 кг и откатывается назад со скоростью u1= 0,3 м/с относительно земли. Коэффициент трения камня о лед равен m =0,06; расстояние, на которое переместился камень, равно s = 15 м. Определить массу конькобежца.
Решение. Конькобежец и камень (рис. 3) составляют замкнутую систему, для которой выполняется закон сохранения импульса
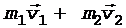
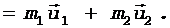 (1)
(1)
Левая часть уравнения (1) представляет собой импульс системы "конькобежец - камень" до толчка, когда камень и конькобежец покоились; правая — после толчка.

Рис. 3
Запишем уравнение (1) в проекциях на горизонтальную ось:
0 = - m1u1 + m2u2
и получим выражение для модуля скорости камня после броска
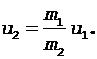 (2)
(2)
При движении камня по льду на него действуют три силы: сила тяжести 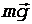 , сила нормальной реакции опоры
, сила нормальной реакции опоры 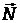 и сила трения
и сила трения 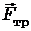 . Первые две силы перпендикулярны к направлению движения и работы не совершают, поэтому работа всех сил будет равна работе силы трения:
. Первые две силы перпендикулярны к направлению движения и работы не совершают, поэтому работа всех сил будет равна работе силы трения:
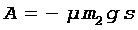 .
.
Изменение кинетической энергии камня в процессе торможения после броска составит
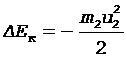 .
.
Используя теорему о кинетической энергии, получим
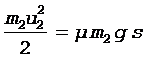 . (3)
. (3)
Переписав формулу (3) с учетом выражения (2):
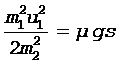 ,
,
получим выражение для расчета искомой величины
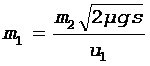 .
.
После подстановки исходных данных имеем
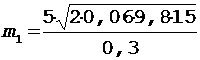 = 70 кг.
= 70 кг.
Пример 6. Нерастяжимая тонкая гибкая нить одним концом закреплена, как показано на рис.4, затем перекинута через невесомый подвижный блок и через неподвижный блок в виде сплошного диска массой m = 6 кг. К подвижному блоку подвешен груз массой m1 = 5 кг, ко второму концу нити подвешен груз массой m2 = 10 кг.
Определить: 1) скорости поступательного движения грузов v1 и v2 , когда они, будучи предоставленными самим себе, придут в движение и правый груз опустится на высоту h = 3,5 м; 2) ускорения a1 и a2 , с которыми будут двигаться грузы; 3) силы натяжения нити. Трением, массой нити и массой подвижного блока можно пренебречь.
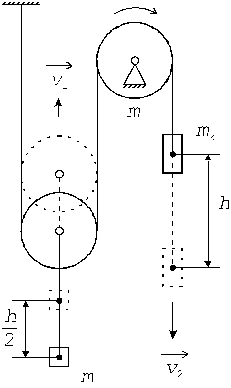 Рис. 4 Рис. 4 | 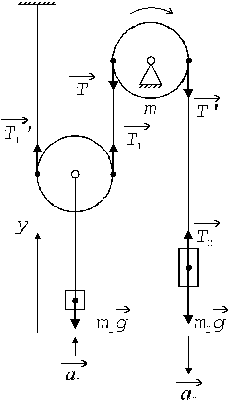 Рис. 5 Рис. 5 |
Решение. На тела системы действуют консервативные силы тяжести и упругости, поэтому выполняется закон сохранения механической энергии:
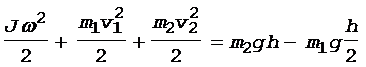 , (1)
, (1)
где w - угловая скорость неподвижного блока;
J - момент инерции неподвижного блока.
Очевидно, что
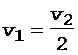 . (2)
. (2)
Скорость поступательного движения правого груза совпадает с линейной скоростью точек, лежащих на ободе неподвижного блока, поэтому
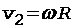 , (3)
, (3)
где R - радиус неподвижного блока.
Момент инерции блока в виде сплошного диска определяется по формуле
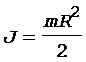 . (4)
. (4)
Перепишем уравнение (1) с учетом формул (2)-(4):
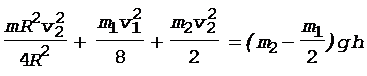 .
.
После преобразований получим
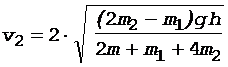 . (5)
. (5)
Подставляя исходные данные в формулу (5), найдем скорость v2:
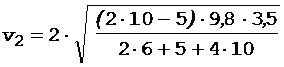 = 6 м/с,
= 6 м/с,
а затем по формуле (2) вычислим v1:
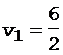 = 3 м/с.
= 3 м/с.
Ускорение второго груза найдем по формуле
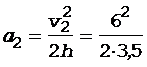 = 5,14 м/с2. (6)
= 5,14 м/с2. (6)
Очевидно, что ускорение первого груза будет вдвое меньше:
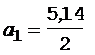 = 2,57 м/с2. (7)
= 2,57 м/с2. (7)
Рассмотрим силы, действующие на тела системы (рис. 5). На первый груз действуют силы натяжения нити 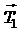 и
и 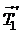 , а также сила тяжести
, а также сила тяжести 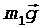 . На второй груз действует сила тяжести
. На второй груз действует сила тяжести 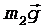 и сила натяжения нити
и сила натяжения нити 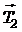 .
.
Направим ось y вертикально вверх и напишем для каждого груза уравнение движения (второй закон Ньютона) в проекциях на эту ось.
Для первого груза
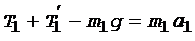 , (8)
, (8)
для второго груза
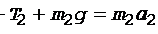 . (9)
. (9)
Момент сил 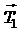 и
и 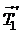 относительно оси подвижного блока равен нулю, так как блок невесомый. Из этого следует, что
относительно оси подвижного блока равен нулю, так как блок невесомый. Из этого следует, что 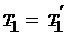 и уравнение (8) может быть переписано в виде
и уравнение (8) может быть переписано в виде
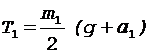 .
.
Найдем Т1 с учетом формулы (7):
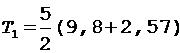 = 30,9 Н. (10)
= 30,9 Н. (10)
Выразим T2 из уравнения (9) и найдем с учетом (6):
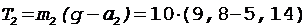 = 46,6 H. (11)
= 46,6 H. (11)
Под действием сил 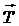 и
и 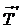 неподвижный блок будет вращаться по часовой стрелке с угловым ускорением e. Согласно основному закону динамики вращательного движения
неподвижный блок будет вращаться по часовой стрелке с угловым ускорением e. Согласно основному закону динамики вращательного движения
T'R - TR = Je . (12)
Угловое ускорение e связано с ускорением второго груза а2 и радиусом неподвижного блока R соотношением
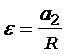 . (13)
. (13)
Подстановка формул (4) и (13) в выражение (12) приводит после сокращения на R к уравнению
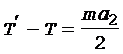 .
.
Это уравнение нужно лишь для проверки правильности ранее найденных значений Т1 и Т2, так как согласно третьему закону Ньютона с учетом невесомости нити имеем
T'= Т2 = 46,6 Н,
Т = Т1 = 30,9 Н.
Пример 7. Горизонтальная платформа в виде сплошного диска массой m1 = 200 кг вращается вокруг вертикальной оси, проходящей через ее центр, с частотой n = 8,5 об/мин. Человек массой m2 стоит при этом в центре платформы. Когда человек перешел на край платформы, она стала вращаться с частотой n’ = 5 об/мин. Найти массу человека, считая его материальной точкой.
Решение. Человек и платформа представляют собой замкнутую систему тел, вращающихся вокруг одной и той же неподвижной оси. Для такой системы справедлив закон сохранения момента импульса
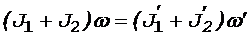 , (1)
, (1)
где J1 и 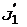 — моменты инерции платформы до и после перехода человека соответственно;
— моменты инерции платформы до и после перехода человека соответственно;
J2 и 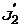 — моменты инерции человека до и после перехода соответственно;
— моменты инерции человека до и после перехода соответственно;
w — угловая скорость платформы и человека до перехода;
w’ — угловая скорость платформы и человека после перехода.
Угловые скорости связаны с частотой вращения соотношениями
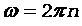 , (2)
, (2)
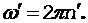 (3)
(3)
Момент инерции платформы (сплошного диска) определяется по формуле
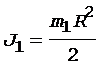 , (4)
, (4)
где R - радиус платформы.
Очевидно, что J1 = 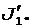 Момент инерции человека (материальной точки), находящегося на краю платформы, определяется по формуле
Момент инерции человека (материальной точки), находящегося на краю платформы, определяется по формуле
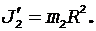 (5)
(5)
Момент инерции человека, стоящего в центре платформы, равен J2 = 0. C учетом этого, а также принимая во внимание формулы (2)-(5), перепишем уравнение (1) в виде
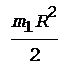
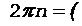
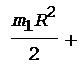
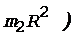
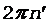 .
.
После сокращений на общие множители и перегруппировки членов получим
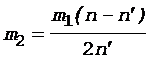 . (6)
. (6)
Подстановка исходных данных в формулу (6) дает
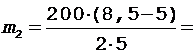 70 кг.
70 кг.
Термодинамика (№№ 231-250)
Пример 1. Кислород массой m = 2 кг занимает объем V1 = 1 м3 и находится под давлением P1 = 0,2 МПа. После нагревания при постоянном давлении он занял объем V2 = 3 м3, а затем его давление в ходе изохорического процесса стало равным P3 = 0,5 МПа. Найти изменение внутренней энергии газа DU, совершенную им работу A и количество теплоты Q, переданной газу. Построить график процесса.
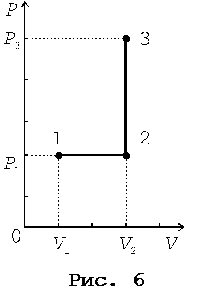 Решение. График процесса приведен на рис. 6.
Решение. График процесса приведен на рис. 6.
Работа расширения газа A12 при изобарическом переходе из состояния 1 в состояние 2 вычисляется по формуле
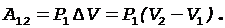
Работа газа A23 при изо-хорическом переходе из сос-тояния 2 в состояние 3 равна нулю.
Таким образом, полная работа A, совершаемая газом при переходе из состояния 1 в состояние 3, равна
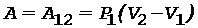 .
.
Изменение внутренней энергии газа при переходе 1®2®3 определяется соотношением
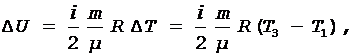 (1)
(1)
где i - число степеней свободы газа;
T1 и T3 - температура газа соответственно в начальном и конечном состояниях.
Уравнения Менделеева - Клапейрона для состояний 1 и 3 запишутся в виде
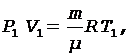 (2)
(2)
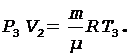 (3)
(3)
После совместного решения уравнений (1)-(3) получим выражение для изменения внутренней энергии газа:
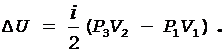
Согласно первому началу термодинамики, теплота Q, переданная газу, расходуется на совершение газом работы и на изменение его внутренней энергии:
Q = A + D1U.
Произведем вычисления, учитывая, что для двухатомных молекул кислорода 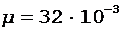 кг/моль, а число степеней свободы i = 5:
кг/моль, а число степеней свободы i = 5:
A = A12 = 0,2×106×(3 - 1) = 0,4×106 Дж = 0,4 МДж;
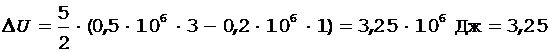 ×МДж;
×МДж;
Q = (3,25 + 0,4) = 3,65 МДж.
Пример 2. Тепловой двигатель, работающий по циклу Карно, получает тепло от нагревателя при температуре 227 °С в количечтве Q1=5 кДж за цикл и передает часть его окружающему воздуху. При этом двигатель совершает за цикл работу, равную 2 кДж.
С каким к.п.д. работает двигатель? Какова температура окружающего воздуха и как изменяется его энтропия за счет работы двигателя в течении одного цикла?
Р е ш е н и е. Коэффициент полезного действия двигателя, работающего по циклу Карно, равен
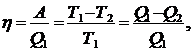 (1)
(1)
где Q2 - тепло, передаваемое двигателем холо-дильнику (окружающей среде);
A - работа;
Т2 – температура холодильника (окружающей среды - воздуха);
Т1 - температура нагревателя.
Отсюда к.п.д.:
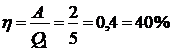 .
.
Температура окружающей среды (Т1=227+273=500К):
Т2=Т1(1-h)=500(1-0,4)=300К=270С.
Изменение энтропии окружающей среды определим по формуле Клаузиуса:
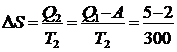 =0,01кДж/К=10Дж/К.
=0,01кДж/К=10Дж/К.
Заметим, что энтропия окружающей среды возрастает, так как она получает тепло от теплового двигателя.
Электростатика
Пример 1. Два точечных электрических заряда q1 = 1 нКл и q2 = - 2 нКл находятся в воздухе на расстоянии d = 10 см друг от друга. Определить напряженность 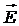 и потенциал j поля, создаваемого этими зарядами в точке А, удаленной от заряда q1 на расстояние r1 = 9 см и от заряда q2 - на расстояние r2 = 7 см.
и потенциал j поля, создаваемого этими зарядами в точке А, удаленной от заряда q1 на расстояние r1 = 9 см и от заряда q2 - на расстояние r2 = 7 см.
Решение. Согласно принципу суперпозиции электрических полей каждый заряд создает поле независимо от присутствия в пространстве других зарядов. Поэтому напряженность электрического поля в искомой точке может быть найдена как геометрическая сумма напряженностей полей, создаваемых каждым зарядом в отдельности: 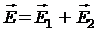 . Напряженности электрического поля, создаваемого в воздухе (e = 1) зарядами q1 и q2, равны
. Напряженности электрического поля, создаваемого в воздухе (e = 1) зарядами q1 и q2, равны
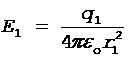 ,
, 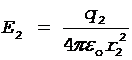 . (1)
. (1)
Вектор 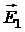 (рис. 7) направлен по силовой линии от заряда q1, так как этот заряд положителен; вектор
(рис. 7) направлен по силовой линии от заряда q1, так как этот заряд положителен; вектор 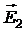 направлен также по силовой линии, но к заряду q2, поскольку этот заряд отрицателен.
направлен также по силовой линии, но к заряду q2, поскольку этот заряд отрицателен.

Модуль вектора 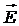 найдем по теореме косинусов:
найдем по теореме косинусов:
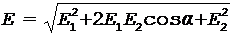 , (2)
, (2)
где a - угол между векторами 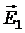 и
и 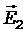 , который мо-жет быть найден из треугольника со сторонами r1, r2 и d:
, который мо-жет быть найден из треугольника со сторонами r1, r2 и d:
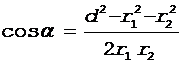 .
.
Во избежание громоздких записей значение cosa удобнее вычислить отдельно:
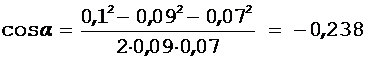 .
.
Подставляя выражения Е1 и Е2 из уравнений (1) в формулу (2) и вынося общий множитель за знак корня, получаем
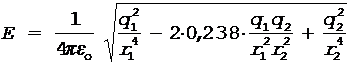 .
.
В соответствии с принципом суперпозиции потен-циал поля, создаваемого двумя зарядами q1 и q2, равен алгебраической сумме потенциалов, т.е.
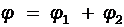 . (3)
. (3)
Потенциал электрического поля, создаваемого в воздухе (e = 1) точечным зарядом q на расстоянии r от него, вычисляется по формуле
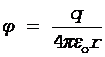 . (4)
. (4)
Согласно формулам (3) и (4),
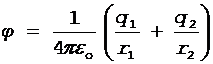 .
.
Учтем, что
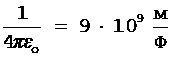 ,
,
и произведем вычисления:
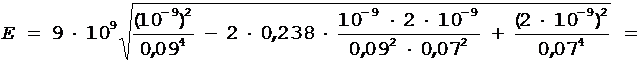
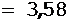 ×103 В/м
×103 В/м 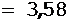 кВ/м.
кВ/м.
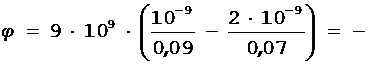 157 В.
157 В.
При вычислении Е знак заряда q2 опущен, так как он определяет направление вектора напряженности, которое было учтено при графическом изображении вектора 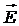 (см. рис. 7).
(см. рис. 7).
Пример 2.Конденсатор емкостью C1 = 3 мкФ был заряжен до разности потенциалов U1 = 40 В. После отключения от источника тока его соединили параллельно с другим незаряженным конденсатором емкостью C2 = 5 мкФ. Какая энергия W израсходуется на образование искры в момент присоединения второго конденсатора?
Решение. Энергия, израсходованная на образование искры, равна
W = W1- W2, (1)
где W1 - энергия, которой обладал первый конден-сатор до присоединения к нему второго конден-сатора;
W2 - энергия, которую имеет батарея, состав-ленная из двух конденсаторов.
Энергия заряженного конденсатора определяется по формуле
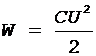 , (2)
, (2)
где C - емкость конденсатора;
U - разность потенциалов между его обкладками.
Выразив в уравнении (1) энергии W1и W2 по формуле (2) и приняв во внимание, что общая емкость параллельно соединенных конденсаторов равна сумме емкостей отдельных конденсаторов, получим
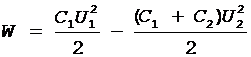 , (3)
, (3)
где U2 - разность потенциалов на зажимах батареи конденсаторов.
Учитывая, что общий заряд q после подключения второго конденсатора остался прежним, выразим разность потенциалов U2 следующим образом:
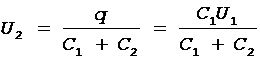 . (4)
. (4)
Подставив выражение (4) в формулу (3), найдем
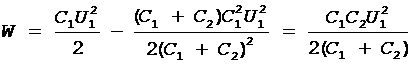 .
.
Произведем вычисления:
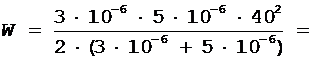 1,5×10-3 Дж.
1,5×10-3 Дж.
Постоянный ток
Пример 1.ПотенциометрссопротивлениемRп= 100 Ом подключен к батарее, ЭДС которой e = 150 В, а внут-реннее сопротивление r = 50 Ом, как показано на рис. 8.
Определить:
1) показание вольтметра, соединенного с одной из клемм потенциометра В и подвижным контактом А, установленным посередине потенциометра, еслисопротивление вольтметраравно RV =500 Ом;
2) разность потенциалов между теми же точками потенциометра при отключении вольтметра.

Решение. Показание вольтметра, подключенного к точкам А и В (рис. 8), или разность потенциалов U1 между точками А и В, определяем по формуле
U1 = I1R1, (1)
где R1 - сопротивление параллельно соединенных вольтметра и половины потенциометра;
I1 - суммарная сила тока в ветвях этого соединения (она равна силе тока в неразветвленной части цепи).
Силу тока I1 найдем по закону Ома для полной цепи:
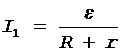 , (2)
, (2)
где R - сопротивление внешней цепи. Оно является суммой двух сопротивлений:
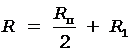 . (3)
. (3)
Перепишем формулу (2) с учетом выражения (3):
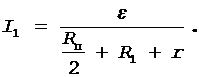 (4)
(4)
Сопротивление R1 найдем по формуле параллельного соединения проводников
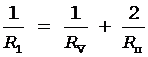 ,
,
откуда
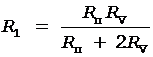 . (5)
. (5)
Произведем промежуточные вычисления по формулам (5),(4) и (1):
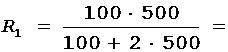 45,5 Ом,
45,5 Ом,
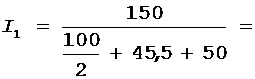 1,03 А,
1,03 А,
U1 = 1,03×45,5 = 46,9 В.
Разность потенциалов между точками А и B при отключенном вольтметре равна произведению силы тока I2 на половину сопротивления потенциометра:
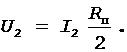 (6)
(6)
Силу тока в цепи при отключенном вольтметре определяем по формуле
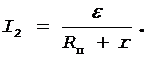 (7)
(7)
Подставив выражение (7) в формулу (6), найдем разность потенциалов U2:
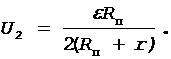
После вычислений получим
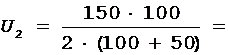 50 В.
50 В.
Пример 2.Найти мощность, выделяемую электри-ческим током в нагрузке R = 25 Ом, если последняя подключена к источнику постоянного тока с внут-ренним сопротивлением r = 0,1 Ом и током короткого замыкания Iк.з = 150 А.
Решение. Записываем выражение для определения мощности, выделяемой на нагрузке R:
P = I2R. (1)
Согласно закону Ома для замкнутой цепи
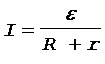 . (2)
. (2)
Запишем соотношение, связывающее ток короткого замыкания Iк.з, ЭДС источника e и его внутреннее сопротивление r:
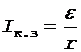 . (3)
. (3)
Отсюда
e = Iк.з r. (4)
Подстановка соотношения (4) в формулу (2) дает
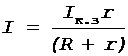 . (5)
. (5)
Переписав формулу (1) с учетом выражения (5), получим окончательную формулу
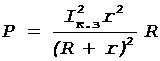 , (6)
, (6)
а затем, подставив числовые значения, найдем
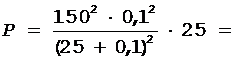 9 Вт.
9 Вт.
Электромагнетизм
Пример 1. Два параллельных бесконечно длинных провода D и С, по которым текут в одном направлении электрические токи силой I = 60 А, расположены на расстоянии d = 10 см друг от друга.

Определить индукцию 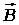 магнитного поля, создаваемого проводниками с током в точке А (рис. 9), отстоящей от оси одного проводника на r1 = 5 см, а от другого - на r2 = 12 см.
магнитного поля, создаваемого проводниками с током в точке А (рис. 9), отстоящей от оси одного проводника на r1 = 5 см, а от другого - на r2 = 12 см.
Решение. Для нахождения магнитной индукции 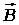 в точке А воспользуемся принципом суперпозиции магнитных полей. Для этого выделим направление магнитных индукций
в точке А воспользуемся принципом суперпозиции магнитных полей. Для этого выделим направление магнитных индукций 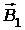 и
и 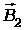 полей, создаваемых каждым проводником в отдельности, и сложим их геометрически:
полей, создаваемых каждым проводником в отдельности, и сложим их геометрически: 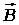 =
=
