Порядок выполнения работы на компьютерной модели

1. На экране монитора в меню «Физическая лаборатория», подведя курсор и щёлкнув левой кнопкой мыши, откройте раздел «Оптика и квантовая физика». Затем этой же кнопкой выберите лабораторную работу «Исследование качества полированной поверхности с помощью микроинтерферометра Линника» и, подведя курсор, активируйте клавишу «Выполнить». При этом откроется окно с изображением и описанием имитируемого прибора. Ознакомившись с прибором, активируйте левой кнопкой мыши клавишу «Выполнить» и войдите в окно с изображением поля зрения окулярного микрометра, вспомогательного рисунка и таблицы, в которую компьютерная программа будет заносить результаты измерений.

2. Выберите в поле зрения окулярного микрометра одну из царапин.

3. Совместите перекрестие окулярного микрометра с центральной линией любой тёмной интерференционной полосы этой царапины (в пределах неискривленного участка линии, т.е. выше или ниже изгиба). Управляйте перекрестием с помощью стрелок клавиатуры.

4. Нажав кнопку «Записать», занесите значение 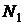в экранную таблицу.

5. Переместите перекрестие на соседнюю центральную линию и, нажав кнопку «Записать», занесите значение 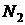в экранную таблицу.

6. Перемещая перекрестие вверх или вниз, а затем вправо или влево наведите его на вершину изгиба этой линии. Нажмите кнопку «Записать», и занесите значение 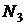в экранную таблицу.

7. Повторите п.п. 3-6 еще два раза, выбирая в качестве начальной линии каждый раз центральную линию другой тёмной интерференционной полосы. Результаты измерений перенесите с экранной таблицы в табл. 1.1 тетради.

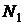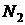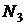8. Нажмите кнопку «Новый опыт» и, выбрав в поле зрения окулярного микрометра новую царапину, повторите п.п. 3-7 с тем, чтобы получить девять наборов параметров , и для трёх царапин.

9. Используя формулы (1.15), (1.16), (1.17) и (1.18) вычислите значения локального интервала между интерференционными полосами 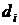, высоты изгиба 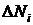, глубины царапины 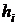, а также среднее значение глубины каждой из трех исследованных царапин .

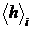10. По формуле (1.19) вычислите усредненное значение глубин царапин по всей исследуемой поверхности 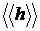, а результаты всех вычислений занесите в табл. 1.1.

11. Используя полученное значение 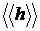и данные табл. 1.2 определите класс шероховатости исследуемой поверхности.

Контрольные вопросы:

1)Какое явление называют интерференцией света? Что такое интерференционная картина?

2) Каковы условия, необходимые для получения интерференционной картины?

3) Какие волны называются когерентными?

4) Опишите методы получения когерентных световых пучков (опыт Юнга, зеркало Ллойда, зеркала Френеля, бипризма Френеля).

5) Что такое оптическая разность хода?

6) Запишите и сформулируйте условия интерференционных максимумов и минимумов для двух синхронно излучающих источников.

7) Что такое интерферометр? Каков принцип работы интерферометра?

8) Почему искривляются интерференционные полосы в интерферометре?

9) Приведите примеры применения интерференции.

10) Почему интерференция считается одним из основных доказательств волновой природы света?

Литература:

1. Найдыш В.М. Концепции современного естествознания: Учебник. — Изд. 2-е, перераб. и доп. – М.: Альфа-М, 2004 г.
2. Трофимова Т.И. Курс физики. – М.: Высшая школа, 2001 г.
3. Бондарев Б.В. Курс общей физики: Учебное пособие. В 3-х кн. Кн. 2. Электромагнетизм. Оптика. Квантовая физика / Б.В. Бондарев, Н.П. Калашников, Г.Г. Спирин. – М.: Высшая школа, 2003 г.
4. ГОСТ 2789‑73* Шероховатость поверхности. Параметры и характеристики.

Лабораторная работа №2

ИССЛЕДОВАНИЕ ТЕПЛОВОГО ИЗЛУЧЕНИЯ
АБСОЛЮТНО ЧЁРНОГО ТЕЛА

Цель работы –исследование температурной зависимости энерге­тической светимости абсолютно чёрного тела.

Приборы и принадлежности– установка ФПК-11, включающая объект исследования – термоизолированную электропечь с отвер­с­тием в передней стенке, моделирующую абсолютно чёрное тело; термостолбик– приёмник теплового излучения; термоэлектрический термометр; измерительное устройство.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Из всех видов излучения наиболее распространённым является температурное, или тепловое.

Тепловым излучением называется электромагнитное излучение, возникающее за счет внутренней энергии излучающего тела и зависящее только от температуры и оптических свойств этого тела.

Тепловое излучение свойственно всем телам при температуре выше абсолютного нуля. Оно имеет сплошной спектр, т.е. содержит элект­ро­магнитные волны всех длин от нуля до бесконечности.

Характерная особенность теплового излучения состоит в том, что в адиабатно замкнутой (теплоизолированной) системе устанавливается тепловое равновесие между тепловым излучением и излучающим телом.

Количественной мерой энергии, излучаемой телом в единицу времени, является поток (мощность) излучения 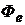, численно равный отношению энергии 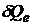, переносимой излучением за малый промежуток времени 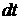, к величине этого промежутка

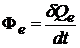. (2.1)

Поток теплового излучения, испускаемый с единицы площади поверхности излучателя в телесный угол 2p во всем интервале длин волн, называется энергетической светимостью тела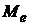

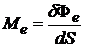. (2.2)

Для характеристики распределения излучения по длинам волн, т.е. для оценки энергетической светимости в единичном спектральном диапазоне, используют спектральную плотность энергетической светимости
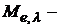физическую величину, численно равную отношению энергетической светимости 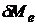в малом спектральном интервале (от 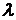до 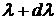) к ширине этого интервала

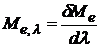. (2.3)

Тогда суммарное излучение тела, т.е. его энергетическую светимость можно рассчитать по формуле

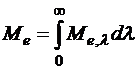(2.4)

При падении на тело поток излучения в общем случае разделяется на три части: одна часть пропускается телом, другая отражается, а третья поглощается и, увеличивая внутреннюю энергию тела, повышает его температуру.

С количественной стороны эти части характеризуются:

Коэффициентом пропускания

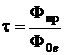, (2.5)

Коэффициентом отражения

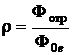(2.6)

и коэффициентом поглощения

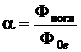, (2.7)

где 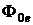– поток (мощность) падающего излучения; Ф_пр – поток прошедшего излучения; Ф_отр – поток отражённого излучения; Ф_погл – поток поглощённого излучения.

Коэффициенты t, r и a зависят от свойств самого тела и длины волны падающего излучения. Спектральная зависимость, т.е. зависимость коэффициентов от длины волны, определяет цвет как прозрачных, так и непрозрачных (t= 0) тел.

Согласно закону сохранения энергии

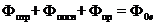. (2.8)

Разделив обе части равенства (2.8) на 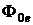, получим:

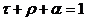(2.9)

Тело, для которого 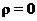, , 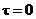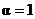называется абсолютно чёрным.

Абсолютно чёрное тело – это тело, которое при любой не разрушающей его температуре полностью поглощает всю энергию падающего на него излучения любой длины волны. Все реальные тела не являются абсолютно чёрными. Однако некоторые из них в определенных интервалах длин волн близки по своим свойствам к абсолютно чёрному телу. Например, в области длин волн видимого света коэффициенты поглощения сажи, платиновой черни и черного бархата мало отличаются от единицы.

Наиболее совершенной моделью абсолютно чёрного тела может служить малое отверстие в замкнутой полости сферической формы. Свет, попадающий через отверстие внутрь полости, будет многократно отражаться от стенок, прежде чем сможет выйти наружу. При каждом отражении свет, независимо от материала стенок, частично поглощается. В результате многократных отражений внутри полости излучение будет практически полностью поглощено, и отверстие снаружи кажется совершенно чёрным. Очевидно, что эта модель тем ближе по характеристикам к чёрному телу, чем больше отношение площади поверхности полости к площади отверстия (рис. 2.1).

Рис. 2.1. Модель абсолютно чёрного тела

Каждое тело может не только испускать, но и поглощать тепловое излучение. Опыты показывают, что чем больше энергии тело излучает при некоторой постоянной температуре, тем сильнее оно поглощает излучение такого же спектрального состава при той же температуре.

Спектральной характеристикой поглощения электромагнитных волн телом является спектральный коэффициент поглощения 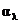– величина, определяемая отношением поглощённого телом потока излучения в малом спектральном интервале (от 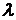до 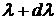) к потоку падающего на него излучения в том же спектральном интервале

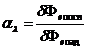. (2.10)

В 1859 г. немецкий физик Густав Кирхгоф (1824-1887гг.) на основании второго начала термодинамики установил один из основных законов теплового излучения.

Закон Кирхгофа: отношение спектральной плотности энергетической светимости равно­весного излучения тела к его спектральному коэффициенту поглощения не зависит от природы тела; для всех тел оно является универсальной функцией длины волны излучения и температуры тела

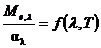. (2.11)

Закон Кирхгофа был подтвержден опытным путём.

Для абсолютно чёрного тела 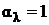. Поэтому из закона Кирхгофа следует, что

,

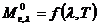где 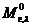– спектральная плотность энергетической светимости абсолютно чёрного тела.

Таким образом, универсальная функция Кирхгофа 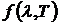представляет собой спектральную плотность энергетической светимости абсолютно чёрного тела. Поэтому выражение закона Кирхгофа (2.11) можно записать в виде

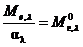. (2.12)

Из формулы (2.12) следует, что:

1) для всех тел отношение спектральной плотности энергетической светимости к спектральному коэффициенту поглощения равно спектральной плотности энергетической светимости абсолютно чёрного тела при тех же значениях 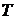и ;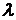

2) спектральная плотность энергетической светимости любого тела в любой области спектра всегда меньше спектральной плотности энергетической светимости абсолютно чёрного тела (при одних и тех же значениях длины волны и температуры);

3) если тело при некоторой температуре не поглощает электромагнитные волны в интервале длин от 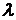до 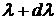, то оно их в этом интервале длин при данной температуре и не излучает;

4) тело, которое при данной температуре сильнее поглощает, должно интенсивнее излучать. Например, при накаливании платиновой пластинки, часть которой покрыта платиновой чернью, её зачернённый конец светится значительно ярче, чем светлый.

Аналитический вид функции 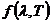для абсолютно черного тела
был установлен учеником Кирхгофа Максом Планком на основе квантовых представлений о природе излучения.

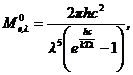(2.13)

где 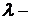длина волны излучения; 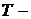температура излучающего тела; 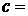3×10⁸ 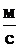– скорость света в вакууме; k = 1,38×10^-23 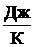– постоянная Больцмана; 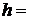6,63×10^-34 Дж×с – постоянная Планка.

Спектр излучения абсолютно черного тела имеет характерный максимум (рис. 2.2), который при повышении температуры сдвигается в коротковолновую часть (рис. 2.3).

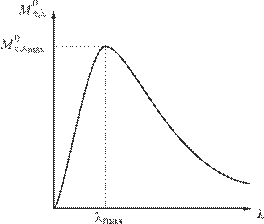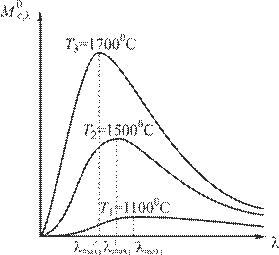Рис. 2.2. Кривая распределения энергии в спектре абсолютно чёрного тела	Рис. 2.3. Кривые спектральной плотности энергетической светимости при различной температуре излучающего тела

Положение максимума спектральной плотноcти энергетической светимости можно определить из выражения (2.13) обычным способом, приравняв к нулю первую производную:

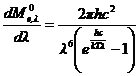
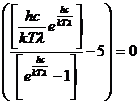. (2.14)

Обозначив 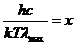, получим:

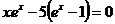. (2.15)

Решение этого трансцендентного уравнения численным методом дает значение 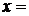4,965.

Следовательно,

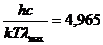, (2.16)

откуда

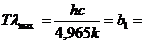2,898· 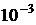м·K, (2.17)

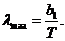(2.18)

где 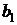– первая постоянная Вина.

Таким образом, функция 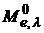достигает максимума при длине волны, обратно пропорциональной термодинамической температуре абсолютно чёрного тела.

Эта зависимость была установлена в 1893 г. немецким физиком Вильгельмом Вином(1864-1928гг.)на основе законовклассической термодинамики и электромагнитной теории света. Её называют законом смещения Вина, подчёркивая тем самым, что с ростом температуры максимум спектральной плотности энергетической светимости сдвигается в сторону меньших длин волн (больших частот).

Из закона Вина следует, что при низких температурах излучаются преимущественно длинные (инфракрасные) электромагнитные волны. По мере же возрастания температуры увеличивается доля излучения, приходящаяся на видимую область спектра, и тело начинает светиться. С дальнейшим ростом температуры яркость свечения увеличивается, а цвет изменяется. Поэтому цвет излучения может служить характеристикой температуры излучения. Примерная зависимость цвета свечения тела от его температуры приведена в табл. 2.1.

Таблица 2.1

Цвет излучения	Красный, едва видимый	Тёмно-красный	Вишнёво-красный	Оранжевый	Белый
Температура, ºС

Подставив формулу (2.18) в выражение (2.13), Вин показал, что максимальное значение функции 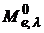пропорционально пятой степени термодинами­ческой температуры тела. Это утверждение носит название второго закона Вина. Он был получен в 1896 году.

Математическое выражение второго закона Вина имеет вид

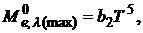(2.19)

где 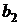– вторая постоянная Вина ( · ).

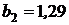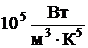В 1911 г. Вильгельм Винбыл удостоен Нобелевской премии по физике за работы по тепловому излучению.

Энергетическую светимость абсолютно чёрного тела можно найти из выражения (2.13) простым интегрированием по длине волны

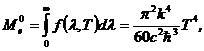(2.20)

где 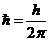– приведённая постоянная Планка,

или

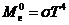(2.21)

где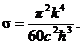

Энергетическая светимость абсолютно чёрного тела пропорциональна четвёртой степени его термодинамической температуры.

Это положение носит название закона Стефана – Больцмана по имени австрийских физиков Йозефа Стефана (1835-1893гг.) и Людвига Больцмана (1844-1906гг.).

Коэффициент пропор­циональности 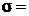5,67×10^-8 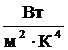называется постоянной Стефана – Больцмана.

Абсолютно чёрное тело является идеализацией реальных тел. Реальные тела испускают излучение, спектр которого не описывается формулой Планка. Их энергетическая светимость, кроме температуры, зависит от природы тела и состояния его поверхности. Эти факторы можно учесть, если в формулу (2.21) ввести коэффициент 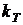, показывающий, во сколько раз энергетическая свети­мость абсолютно чёрного тела при данной температуре больше энер­гетической светимости реального тела при той же температуре

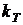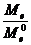= , (2.22)

откуда ,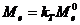

или 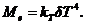(2.23)

Для всех реальных тел 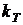<1 и зависит как от природы тела и состояния его поверхности, так и от температуры. В частности, для вольфрамовых нитей электроламп накаливания зависимость 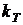от 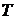имеет вид, представленный на рис. 2.4.

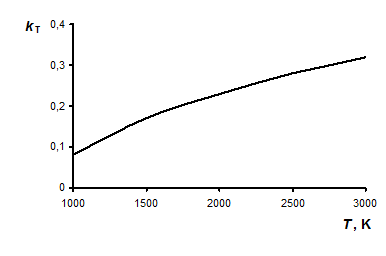
Рис. 2.4. Зависимость 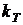от температуры 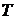тела

МЕТОДИКА ИЗМЕРЕНИЯ

Измерение энергии излучения и температуры электропечи основано на эффекте Зеебека, заключающемся в возникновении электродвижущей силы в электрической цепи, состоящей из нескольких разнородных проводников, контакты которых имеют различную температуру.

Два разнородных проводника образуют термопару, а последовательно соединенные термопары – термостолбик. Если контакты (обычно спаи) проводников находятся при различных температурах, то в замкнутой цепи, включающей термопары, возникает термоЭДС, величина которой однозначно определяется разностью температур горячих и холодных контактов, количеством последовательно соединенных термопар и природой материалов проводников.

Величина термоЭДС, возникающей в цепи за счет энергии падающего на спаи термостолбика излучения, измеряется милливольтметром, размещенным на передней панели измерительного устройства. Шкала этого прибора проградуирована в милливольтах.

Температура абсолютно чёрного тела (печи) измеряется с помощью термоэлектрического термометра, состоящего из одной термопары. Её ЭДС измеряется милливольтметром, также расположенным на передней панели измерительного устройства и проградуированным в °С.

Примечание. Милливольтметр фиксирует разность температур горячего и холодного спаев термопары, поэтому для получения температуры печи необходимо к показанию прибора прибавить значение температуры в помещении.

В данной работе проводят измерение термоЭДС термостолбика, величина которой пропорциональна энергии, затраченной на нагревание одного из контактов каждой термопары столбика, и, следовательно, энергетической светимости (при равных интервалах времени между измерениями и неизменной площади излучателя):

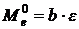, (2.24)

где 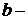коэффициент пропорциональности.

Приравнивая правые части равенств (2.21) и (2.24), получаем, что

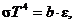
откуда ,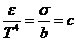

где 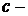постоянная величина.

Одновременно с измерением термоЭДС термостолбика измеряют разность температур 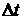горячего и холодного спаев термопары, помещенной в электропечь, и определяют температуру печи.

Используя экспериментально полученные значения температуры абсолютно черного тела (печи) и соответствующие им значения термоЭДС термостолбика, определяют значение коэффициента пропорциональности 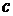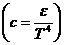, которое во всех опытах должно быть одинаковым. Затем строят график зависимости 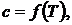который должен иметь вид прямой, параллельной оси температур.

Таким образом, в лабораторной работе устанавливаетсяхарактер зависимости энергетической светимости абсолютно черного тела от его температуры, т.е. проверяется закон Стефана–Больцмана.