Элементы физики твердого тела

· Т = Θ = 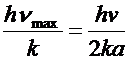- температура Дебая

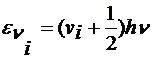· - энергия фонона

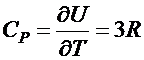· -закон Дюлонга – Пти

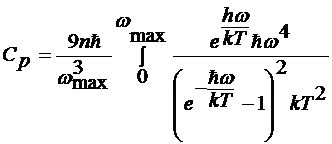· - формула теплоёмкости Дебая

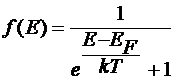· - функция Ферми – Дирака

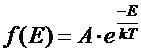· - функция Максвелла – Больцмана

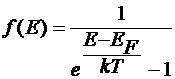· - функция распределения Бозе – Эйнштейна

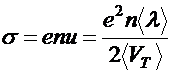· - электропроводность по квантовой теории

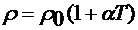· -зависимость удельного сопротивления от температуры

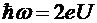· - эффект Джозефсона

· < n > ≈ 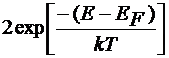- заполнение зоны электронами

· < n > ≈ 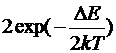- среднее число электронов проводимости

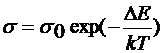· - проводимость собственного полупроводника

Примеры решения задач

Пример 1.Определить число атомов меди в 1м³. Плотность меди ρ = 8.93٠10³кг/м³, атомная масса меди μ = 63.546г, N_A = 6.022٠10²³.

Решение

Дано:

ρ = 8.93٠10³кг/м³

μ = 63.546г

N_A = 6.022٠10²³

n = ?

m = ρV 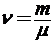общее число атомов в массе m будет n = νN_A = =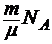

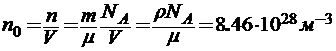
Ответ: .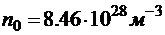

Пример 2.Вычислить скорость дрейфа зарядов при прохождении тока силой 1А через медный провод сечением 1мм².

Решение

Дано:

I = 1A

S = 1мм²

= ?

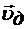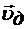Плотность тока непосредственно связана с концентрацией и скоростью движения зарядов: 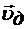‑ скорость дрейфа. За время 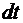заряды пройдут расстояние 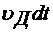. Значит количество носителей заряда, которое пройдет через площадку 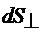будет 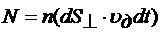, а перенесенный заряд ‑ 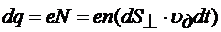, где 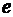‑ элементарный заряд. Тогда

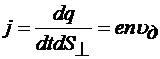
Из приведенного соотношения

.

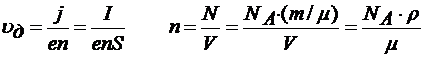Подставляя значение плотности меди 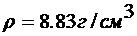и молярной массы 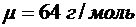, после вычисления получим .

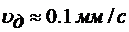Ответ: .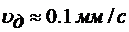

Пример 3.Определить среднеквадратичную скорость V_кв хаотического теплового движения свободных электронов в металле при Т = 300ºК.

Решение

Дано:

Т = 300ºК

V_кв = ?

Из курса молекулярной физики известно, что ,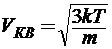

где k = 1.38٠10^-23Дж/К- постоянная Больцмана,

m – масса частицы (в данном случае m = 9.11٠10^-31кг).

Откуда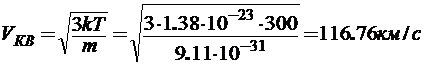

Ответ: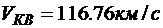

Пример 4. Определить функцию распределения N(E) для электронов на уровне Е для случая Е − Е_F<< kT если распределение описывается статистикой 1) Ферми-Дирака, 2) Максвелла-Больцмана.

Решение

Дано:

Е − Е_F<< kT

N(E) = ?

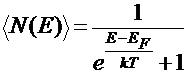- функция Ферми – Дирака

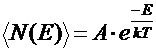- функция Максвелла – Больцмана

Для случая Е − Е_F<< kT имеем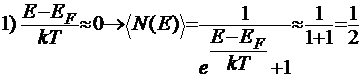

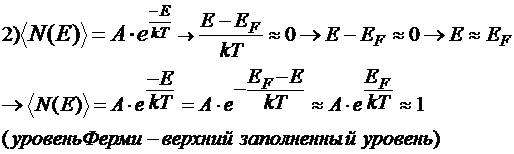
Ответ: 1) N(E) =0.5, 2) N(E) =1.

Пример 5. Определить ширину запрещённой зоны собственного полупроводника , если при температуре Т₁ его сопротивление равно R₁, а при температуре Т₂ − R₂.

Решение

Дано:

Т₁, Т₂

R₁, R₂.

∆Е = ?

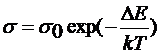- проводимость собственного полупроводника

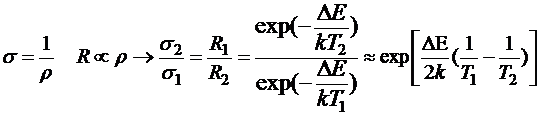. Откуда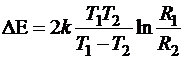

Ответ: .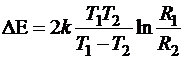

Пример 6.Определить максимальную энергию фонона, возбуждённого в кристалле NaCℓ, если температура Дебая для него T_D =320 K. Фотон какой длины волны обладал бы такой энергией?

Решение

Дано:

T_D =320 K

λ = ?

ε = ?

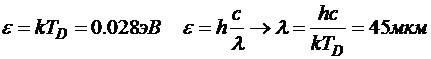
Ответ: .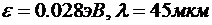

Пример 7. В чём отличие и сходство теорий теплоёмкости твёрдых тел Эйнштейна и Дебая?

Решение

Основным вопросом теории теплоёмкости твёрдых тел является вопрос о зависимости теплоёмкости от температуры.

Все теории теплоёмкости представляют кристалл как совокупность гармонических осцилляторов с частотой ν.

Теория теплоёмкости, основанная на классических представлениях о равновероятном распределении энергии по степеням свободы в состоянии термодинамического равновесия (kT на одну степень свободы) приводит к выражениюU = 3N_AkT = 3RT для внутренней энергии тела. Откуда 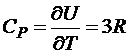. Это – закон Дюлонга – Пти, согласно которому молярная теплоёмкость всех химически простых тел в кристаллическом состоянии одинакова и равна 3R (R – универсальная газовая постоянная).

Этот закон справедлив только при высоких температурах и не согласуется с экспериментом при низких температурах.

При низких температурах теплоёмкость кристаллов убывает, стремясь к 0 при Т = 0ºК.