Теория активных столкновений

Теория активных столкновений (она также называется теорией активных соударений) явилась первой теорией, количественно объяснившей данные кинетических исследований на основе молекулярно-кинетических представлений. Эта теория разработана как для случая бимолекулярных столкновений, так и для тримолекулярных столкновений. Ниже рассматриваются основные результаты, полученные для бимолекулярных столкновений.

В основе теории использованы следующие предположения (постулаты теории активных соударений):

1) Первым актом возможного взаимодействия молекул является их столкновение.

2) Столкновение молекул может служить причиной превращения молекул только в том случае, если энергия столкновения превышает или по крайней мере равна некоторой критической величине e_а. Столкновения с энергией, равной этой величине или превышающей ее, называются активными.

3) Активные столкновения приводят к благоприятному исходу, то есть к началу химической реакции, если расположение молекул в момент столкновения соответствует данной реакции.

Первый постулат теории означает, что теория не рассматривает реакции, протекающие под непрерывным воздействием квантов света или частиц высокой энергии (гамма-квантов, электронов и т.д.).

Второй постулат теории предполагает, что для начала химического превращения сталкивающиеся молекулы должны обладать энергией, достаточной для преодоления вполне определенного энергетического барьера. Если энергия столкновения молекул оказывается меньше e_а, то происходит упругий удар без каких-либо химических превращений.

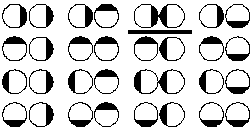Рис. 12 - 1. Условное представление положений молекул в момент столкновения.

Из третьего постулата следует, что не все активные столкновения эффективны. На рис. 12 - 1 условно показаны возможные положения двух молекул в момент столкновения. Условные благоприятные для реакции положения на рисунке подчеркнуты. Отношение числа положений, благоприятствующих химической реакции, к общему числу возможных положений молекул в момент столкновения называется стерическим фактором. Расчеты показывают, что обычно величина стерического фактора близка к 10⁻².

Молекулярно-кинетическая теория дает возможность рассчитывать число столкновений с определенной энергией.

Общее число столкновений Z₀ в единичном объеме газовой фазы определяется уравнением:

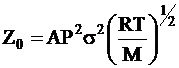, (12 - 1)

в котором A - числовой коэффициент, P - давление, s - эффективный диа­метр столк­нове­ния, M - эффективная молярная масса сталкивающихся моле­кул.

Объединив все характеристики сталкивающихся молекул с числовым коэффициентом в единую константу для данной реакции b, уравнение (12 - 1) можно записать в следующей форме:

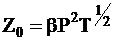. (12 - 2)

Число столкновений с энергией e_i подчиняется распределению Больцмана:

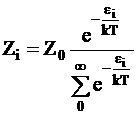. (12 - 3)

Число активных столкновений в единичном объеме представляет собой сумму всех столкновений, энергия которых не меньше e_а: _______________________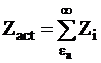

или

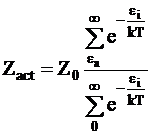. (12 - 4)

Число первичных химических превращений за единицу времени в единичном объеме в соответствии с третьим постулатом теории окажется равным:

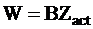, (12 - 5)

а с учетом уравнений (12 - 2) и (12 - 4):

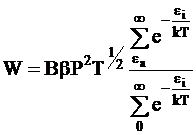. (12 - 6)

Для бимолекулярной реакции в газовой фазе зависимость скорости от давления выражается уравнением:

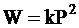. (12 - 7)

Сравнивая уравнения (12 - 6) и (12 - 7), получим уравнение для константы скорости реакции:

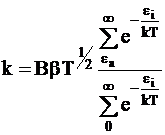. (12 - 8)

Прологарифмируем уравнение (12 - 8):

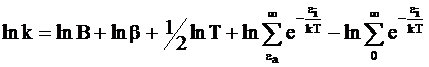
и продифференцируем по температуре:

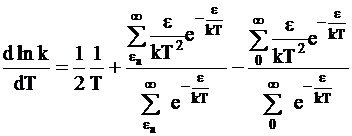. (12 - 9)

Пренебрегая в первом приближении величиной 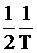и проведя преобразования, получим:

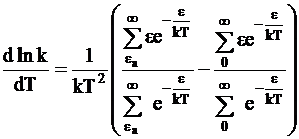. (12 - 10)

Для выяснения смысла отношений сумм, заключенных в скобках в правой части уравнения (12 - 10), отметим, что энергия всех активных соударений X_act равна:

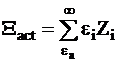. (12 - 11)

С учетом уравнения (12 - 3) равенство (12 - 11) приобретает следующий вид:

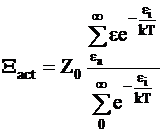. (12 - 12)

Отношение полной энергии активных столкновений к числу всех активных столкновений представляет собой среднюю энергию активного столкновения:

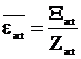. (12 - 13)

Сравнение уравнений (12 - 4), (12 - 12) и (12 - 13) показывает, что первое отношение сумм в уравнении (12 - 10) представляет собой среднюю энергию активного соударения:

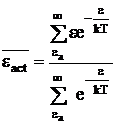. (12 - 14)

Второе отношение сумм представляет среднюю энергию всех столкновений в системе:

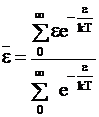. (12 - 15)

Равенства (12 - 14) и (12 - 15) позволяют представить уравнение (12 - 10) следующим образом:

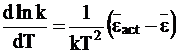. (12 - 16)

Умножение числителя и знаменателя правой части уравнения (12 - 16) на постоянную Авогадро дает:

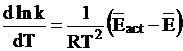, (12 - 17)

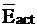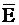где и - соответственно средняя энергия 1 моль активных соударений и средняя энергия 1 моль всех соударений.

Сравнение уравнения Аррениуса в дифференциальной форме (11 - 7) и уравнения (12 - 17) позволяет установить, чем же в соответствии с теорией активных соударений является энергия активации.

Энергия активации равна разности средней энергии 1 моль активных соударений и средней энергии 1 моль всех соударений:

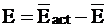. (12 - 18)

Напомним, что уравнение (12 - 18) имеет приближенный характер, так как при его выводе была исключена производная 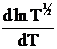. Уточненное значение энергии активации E_A со значением величины E выражается соотношением:

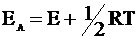. (12 - 19)

Иная трактовка энергии активации дается теорией активированного комплекса, которая будет рассмотрена в дальнейшем.

12 - 2. Механизм мономолекулярных реакций по теории активных столкновений (схема Линдемана)

Формальная кинетика предполагает, что порядок реакции зависит от молекулярности самой медленной стадии. Согласно теории активных столкновений химическая реакция начинается с соударения двух (значительно реже - трех) молекул. Так как большая часть реакций имеет первый порядок, то это означает, что реакция не ограничивается только столкновением двух частиц.

Механизм реакции, объясняющий появление первого порядка при столкновении двух молекул, был предложен Линдеманом в 1922 г. и называется схемой Линдемана.

Согласно этой схеме столкновение двух молекул не приводит к мгновенному химическому превращению, а его результатом является перераспределение энергии молекул в момент удара и образование частицы с избыточной энергией А*:

k₁

А + А ¾® А* + А. (I)

Частица с избыточной энергией А* (ее можно также называть возбужденной молекулой) способна претерпевать дальнейшее превращение до продукта В:

k₂

А* ¾® В. (II)

Кроме того, сталкиваясь с другими частицами, активная частица А* может вернуть избыток энергии и вернуться в исходное состояние:

k _-1

А* + А ¾® А + А. (III)

Всю совокупность реакций можно представить следующим образом: k₁

А + А D А* + А. (IV)

k _-1 ¯ k₂

В

Скорость накопления активных частиц в соответствии с этой схемой описывается уравнением:

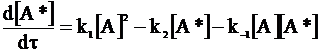(12 - 20)

Зависимость концентрации активных частиц от времени с начала реакции показана на рис. 12 - 2.

Как видно из рис. 12 - 2, вначале концентрация активных частиц в течение короткого времени очень быстро возрастает, затем в течение длительного времени медленно уменьшается. Производная концентрации по времени до точки максимума по абсолютной величине может во много раз превышать производную концентрации по времени после точки максимума. В связи с этим, сравнивая производную после достижения максимума с производной на начальном участке кривой, можно для убывающей части кривой принять:

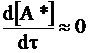. (а)

Условие (а) называется квазистационарным состоянием.

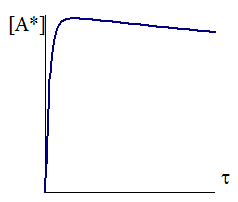Рис. 12 - 2. Изменение концентра­ции промежуточного вещества со временем.

При квазистационарном состоянии уравнение (12 - 20) принимает следующий вид:

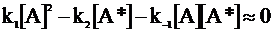. (12 - 21)

Решение уравнения (12 - 21) относительно концентрации активных частиц дает:

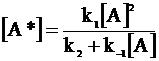. (12 - 22)

Скорость образования вещества В характеризуется уравнением:

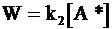
или

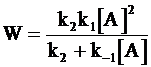. (12 - 23)

Если константа скорости k₂ окажется достаточно большой, чтобы выполнялось условие k₂ >> k₋₁[A], то уравнение (12 - 23) превращается в уравнение скорости реакции второго порядка:

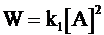. (12 - 24)

В случае очень малой константы k₂ выполняется условие: k₂ << k₋₁[A], а уравнение (12 - 23) превращается в уравнение скорости реакции первого порядка:

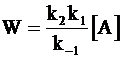. (12 - 25)

Полученные результаты легко объяснимы.

Если скорость превращения активной частицы очень велика, то она существует крайне непродолжительное время и не успевает сталкиваться с другими частицами. В этом случае скорость реакции определяется только стадией (I) и реакция является бимолекулярной.

Если частица, не превращаясь, существует в течение длительного времени, то велика вероятность ее столкновения с другими частицами. В этом случае скорость реакции возрастает вместе с увеличением скорости накопления промежуточных активных частиц и скорости их превращения в продукты реакции и убывает с ростом скорости превращения активных частиц в исходные неактивные.

Схема Линдемана подтверждается данными, полученными при изучении реакций в газовых фазах.

При очень низких давлениях газа столкновения активных частиц с другими молекулами происходят редко и они успевают превратиться в продукты реакции. В этом случае следует ожидать второй порядок реакции. При высоких давлениях частота столкновений возрастает и полностью выполняется условие: k₂ << k₋₁[A], а реакция описывается уравнением (12 - 15). Опыт показал, что проводя реакцию от давлений в несколько сотых мм рт. ст. (от нескольких Па) до десятков атмосфер (несколько МПа), можно наблюдать переход от кинетики реакции второго порядка до реакции первого порядка.

12 - 3. Теория переходного состояния (теория активного комплекса)

В основе теории переходного состояния используются следующие положения (постулаты теории).

1) Столкновение частиц приводит к образованию связи между ними.

Неустойчивое состояние, в котором существуют связи между всеми частицами, называется переходным состоянием. Его также представляют как комплекс, временно образуемый взаимодействующими частицами, и называют активным комплексом.

Образование и распад активного комплекса происходит только в одном направлении (см. рис. 12 - 3).

2) Порядок образования и распада комплекса таков. Взаимодействующие частицы движутся друг к другу до тех пор, пока между ними не возникнет дополнительная связь, образование которой приводит к ослаблению связи, уже существующей в одной из взаимодействующих молекул. Затем частицы начинают расходиться. Ослабленная ранее существовавшая связь исчезает, а возникшая при сближении частиц новая связь остается.

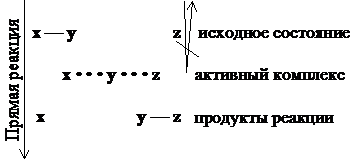Рис. 12 - 3. Образование и распад активного комплекса.

Данный постулат запрещает распад активного комплекса на исходные частицы. Он может распадаться только с образованием продуктов реакции.

3) Образование активного комплекса не приводит к нарушению распределения частиц по скоростям и энергиям Максвелла - Больцмана.

4) Предполагается, что смещение электронных орбиталей в частицах при образовании активного комплекса происходит во много раз быстрее, чем движение атомных ядер.

Этот постулат теории переходного состояния называется принципом адиабатности. Он лежит в основе расчетов энергии взаимодействующих частиц, так как предполагает, что электроны всегда успевают принять наиболее устойчивую конфигурацию для задаваемого расстояния между центрами атомов.

Покажем, как могут быть использованы вышеприведенные постулаты для вывода основного уравнения теории переходного состояния.

Пусть протекает, как показано на рис. 12 - 3, реакция:

XY + Z = X + YZ .

Формально скорость этой реакции определяется уравнением:

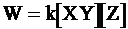. (12 - 26)

С другой стороны, скорость образования продуктов реакции определяется числом распадающихся в единицу времени активных комплексов по схеме:

k_A.C.

X××× Y×××Z ¾® X + YZ.

Так как распад комплекса является мономолекулярной реакцией, то для ее скорости можно записать следующее выражение:

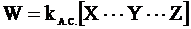. (12 - 27)

Используя уравнение (9 - 20), связывающее константу скорости необратимой реакции первого порядка со средним временем жизни превращаемого вещества 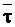, равенство (12 - 27) можно представить следующим образом:

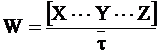. (12 - 28)

Сравнивая равенства (12 - 26) и (12 - 28), получим:

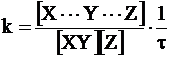. (12 - 29)

Уравнение (12 - 29) является основным уравнением для расчета константы скорости реакции. Однако оно может получить окончательную форму, если выразить входящие в него величины через энергетические характеристики.

Среднее время жизни комплекса можно оценить, используя второй постулат теории.

Так как образование и распад комплекса происходят только в одном направлении, то его существование можно представить в виде одного колебательного цикла по новой связи. Энергия таких колебаний равна:

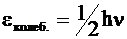, (12 - 30)

где h - постоянная Планка.

Энергия, необходимая для возбуждения колебаний, равна кинетической составляющей сталкивающихся частиц. При движении частиц вдоль одной оси она равна:

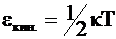, (12 - 31)

где k - постоянная Больцмана.

Из равенства кинетической энергии и энергии колебаний следует:

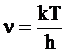. (12 - 32)

Частота колебаний представляет собой величину, обратную периоду одного колебания, а принимая во внимание, что комплекс существует только в течение одного колебательного цикла, имеем:

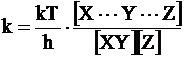. (12 - 33)

При сохранении равновесного распределения скоростей и энергий частиц соотношение между концентрациями исходных веществ и активного комплекса определяется константой K^#:

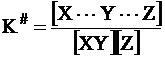. (12 - 34)

Константа К^# не является истинной константой равновесия, так как комплекс не распадается в обратном направлении (на исходные частицы). Однако соотношение между концентрациями зависит от энергии частиц в исходном состоянии и в состоянии активного комплекса. В этом случае можно воспользоваться уравнением изотермы химической реакции в следующей форме (см. часть I, стр. 77):

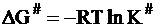. (12 - 35)

Изменение энергии Гиббса для перехода из исходного состояния частиц в состояние активного комплекса (переходное состояние) DG^# определяется изменением энтальпии DH^# и изменением энтропии DS^#:

.

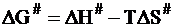Следовательно, константа К^# может быть представлена следующим образом:

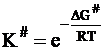
или

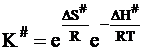. (12 - 36)

Таким образом, уравнение для константы скорости реакции приобретает вид:

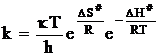. (12 - 37)

Величина 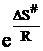, содержащая энтропию активации DS^#, соответствует стерическому множителю В теории активных столкновений. Энтальпия активации DH^# в теории переходного состояния соответствует энергии активации. Для ее расчета необходимо знать энергию системы в исходном состоянии и энергию активированного комплекса.

Для расчета изменения энергии системы при переходе из исходного состояния в переходное необходимо найти зависимость энергии системы от расстояний между атомами. В рассматривавшемся случае образования активного комплекса из исходной молекулы XY и частицы Z независимыми переменными служат расстояния между центрами атомов в паре X и Y, которые обозначим r_XY, и расстояние между центрами атомов Y и Z, которое обозначим r_YZ. Энергия системы является функцией этих переменных:

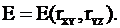
В системе трех координат эта зависимость передается поверхностью. Для представления зависимости энергии от расстояний r_XY и r_YZ на плоскости используется такой же метод, что и при построении топографических карт, а именно: проводятся равноотстоящие друг от друга плоскости, перпендикулярные оси энергии, а линии пересечения этих плоскостей с поверхностью наносятся на плоскость чертежа. На рис. 12 - 4 показан пример построения энергетической диаграммы по этому методу.

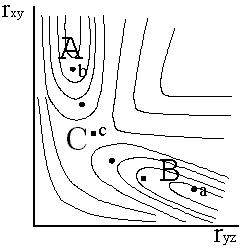Рис. 12 - 4. Энергетическая диа­грамма трехатомной системы.

Для построения диаграммы рассчитывают потенциальную энергию системы для различных сочетаний расстояний r_XY и r_YZ. При этом используется четвертый постулат теории (принцип адиабатности), в соответствии с которым расчеты проводятся для систем с равновесными электронными конфигурациями. Молекула XY имеет минимум энергии при расстоянии между атомами, равном длине связи. Увеличение или уменьшение этого расстояния приводит к возрастанию энергии в отдельной молекуле. То же относится и к молекуле YZ. Следовательно, на диаграмме должны быть две области с пониженными значениями энергии А и В (их образно называют долинами). Области А и В отделены друг от друга участком небольшого подъема энергии С (его образно называют перевалом).

На типичной энергетической диаграмме (рис. 12 - 4) имеется несколько особых точек. Первая из них a отвечает исходному состоянию системы (состоянию до начала реакции). В этом состоянии расстояние между центрами атомов X и Y должно быть равно нормальной длине связи в устойчивом состоянии молекулы XY. Расстояние между центрами атомов Y и Z должно быть очень большим, так как частица Z еще не вступила во взаимодействие с молекулой XY. Еще одна характерная точка b отражает конечное состояние системы (состояние после реакции). Ей соответствует расстояние между центрами атомов Y и Z, равное длине связи во вновь образовавшейся молекуле, и большое расстояние между отделившейся частицей X и атомом Y. Третьей важнейшей точкой на энергетической диаграмме является точка перевала с. Именно в точке перевала существует полностью сформировавшийся активный комплекс.

Из изложенного следует, что химическое превращение согласно теории переходного состояния представляет собой переход из точки а в точку b через точку с. Такой переход происходит при минимальных значениях энергии (на энергетической диаграмме ему соответствует движение из точки а по дну долины А до перевала с, а затем спуск в долину В и движение до точки b). Он называется путем реакциии показан пунктирной линией.

Если разрезать пространственную энергетическую диаграмму по пути реакции перпендикулярно плоскости r_XY - r_YZ, то в разрезе получится линия, длина которой соответствует длине пути реакции, а ордината - энергии системы. Назовем линию в этих координатах профилем пути реакции(рис. 12 - 5).

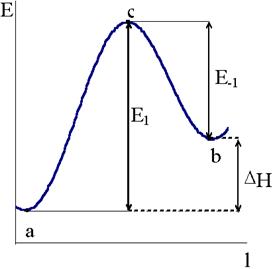Рис. 12 - 5. Энергетический профиль пути реакции.

Разность между энергией системы в переходном состоянии и энергией в исходном состоянии Е₁, как показано на рис. 12 - 5, представляет собой классическую энергию активации прямой реакции. Разность энергий в состоянии активного комплекса и конечном состоянии Е₋₁, равна энергии активации обратной реакции. Разность между энергиями активации прямой и обратной реакций соответствует тепловому эффекту реакции DН.

Таким образом, энергия активации в теории переходного состояния имеет четкую трактовку как величина энергетического барьера, равная разности энергий в переходном и исходном состояниях.

Как уже неоднократно отмечалось, все расчеты потенциальной энергии системы возможны лишь в том случае, когда электроны имеют равновесные конфигурации. В ходе реакции принцип адиабатности нарушается. Поэтому расчетное значение энергии оказывается завышенным. Для учета расхождения между расчетными и реальными значениями энергии в состоянии активного комплекса вводится поправочный коэффициент, который называется трансмиссионным коэффициентомc. С введением этой поправки основное уравнение теории переходного состояния принимает окончательный вид:

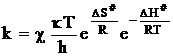. (12 - 38)

Теория переходного состояния применима не только к химическим превращениям, но и к другим кинетическим процессам: диффузии, вязкому течению, электрической проводимости растворов. Предполагается, что движение частиц в жидкости связано с преодолением энергетического барьера, величина которого равна энергии активации.