Изучение корпускулярно-волнового дуализма материи
Материя – бесконечное множество всех сосуществующих в мире объектов и систем, совокупность их свойств, связей, отношений и форм движения. При этом она включает в себя не только все наблюдаемые объекты и тела природы, но и все те которые не даны человеку в ощущениях. Окружающий мир – это движущаяся материя в бесконечно разнообразных формах и проявлениях, со всеми свойствами, связями и отношениями. Все объекты в мире обладают внутренней упорядоченностью и системной организацией. Исходя из системного подхода к природе, материя делится на два больших класса материальных систем: живую и неживую природу.
В живой природе основными элементами выступают белки и нуклеиновые кислоты, клетка и одноклеточные организмы, многоклеточные организмы, органы и ткани, популяции, биоценоз, живое вещество планеты. В системе неживой природы структурными элементами являются элементарные частицы, атомы, молекулы, поля, макроскопические тела, планеты и планетарные системы, звезды и звездные системы, галактики, метагалактики и Вселенная в целом.
Как известно, классическая физика исходит из коренного различия между понятиями частицы и волны. Считается, что частица обладает конечным числом степеней свободы, строгой траекторией движения, отсутствием интерференции и дифракции. Волна же обладает бесконечным числом степеней свободы, отсутствием траектории, ибо каждая точка пространства, куда приходит возбуждение, сама становится источником вторичных волн. Явление интерференции и дифракции – не что иное, как наложение друг на друга когерентных волн; то есть эти явления отражают волновую природу конкретных материальных процессов.
Вся классическая физика строится исходя из представлений о непрерывной природе пространства, времени, движения, непрерывного характера изменения всех физических величин. Гениальная гипотеза, высказанная М. Планком в связи с разрешением кризисной ситуации, которая сложилась в физике в конце XIX века при исследовании законов излучения абсолютно черного тела, постулирует, что вещество не может излучать или поглощать энергию иначе как конечными порциями (квантами), пропорциональными излучаемой (или поглощаемой) частоте. Энергия одной порции (кванта)
E = hn,
где n - частота излучения, а h – универсальная константа, получившая название постоянной Планка, или элементарного кванта действия. Открытие Планка не перечеркивало ряд эффектов, в которых свет проявляет свои волновые свойства. Но при этом были открыты явления, свидетельствующие о корпускулярной природе света. К таким явлениям относится фотоэффект – испускание веществом электронов под воздействием электромагнитного излучения. Таким образом, заговорили о корпускулярно-волновом дуализме света: в одних ситуациях свет ведет себя как волна; а в других ситуациях свет ведет себя как поток частиц (фотонов).
В 1924 году известный французский физик Луи де Бройль распространил идею о двойственной корпускулярно-волновой природе света на все материальные объекты. Согласно де Бройлю,любой частице материи можно поставить в соответствие волну, длина которой обратно пропорциональна импульс частицы:
l = h/p
где l - длина волны, p –импульс частицы, равный произведению ее массы на скорость: p = mv, h – постоянная Планка.
Экспериментально эта гипотеза была подтверждена в 1927 году американскими физиками К. Девиссоном и Л. Джермером, впервые обнаружившими явление дифракции электронов в кристалле никеля. Как мы уже знаем, явление дифракции свидетельствует о типично волновом характере явления. Впоследствии такая же дифракционная картина была обнаружена у протонов, нейтронов и других элементарных частиц при прохождении ими через дифракционную решетку.
Таким образом, было установлено, что материальные частицы, такие, как электрон, протон, нейтрон и другие, обладают не только корпускулярными, но и волновыми свойствами. Это принципиально новое явление было названо корпускулярно-волновым дуализмом.
Лабораторная работа №1А
Определение длины волны при помощи дифракционной решетки
Дифракция света
Развитие оптики вплоть до начала XX века базировалось в основном, на представлении о прямолинейности распространения света. Но уже в XVII веке были известны факты, указывающие на отступление от закона прямолинейного распространения. Это бывает в следующих случаях: когда луч света проходит через малое отверстие в непрозрачном экране; если на пути луча находится малое непрозрачное тело и если свет проходит около края непрозрачного предмета.
Если пучок параллельных лучей света встречает на своем пути непрозрачное круглое тело, то при достаточно малых размерах тела на экране, в середине геометрической тени, будет заметно светлое пятно в центре чередующихся темных и светлых колец. Это указывает на то, что свет распространяется и в область геометрической тени.
Если же пучок параллельных лучей света пропустить через достаточно малое круглое отверстие, то на экране, начиная с некоторого расстояния, по мере изменения расстояния между отверстием и экраном, будет появляться то светлое , то темное пятно в центре чередующихся темных и светлых колец, диаметр которых значительно больше диаметра отверстия. Свет здесь распространяется в область геометрической тени.
Явление отклонения света от прямолинейного распространения в однородной среде, выражающееся в распространении света в область геометрической тени, называется дифракцией света.
Дифракция света показывает, что законы геометрической оптики, базирующиеся на законе прямолинейности распространения света, так же как и ряд других законов физики, оказываются справедливыми только в известных условиях.
Дифракционная решетка
Для получения ярких дифракционных спектров применяются дифракционные решетки. Дифракционная решетка представляет собою совокупность большого числа узких параллельных щелей одинаковой ширины, расположенных на равных расстояниях друг от друга. Простейшим примером дифракционной решетки является стеклянная пластинка, на которой делительной машиной нанесен ряд параллельных штрихов. Места прочерченные машиной являются практически непрозрачными промежутками. Неповрежденные части пластинки играют роль щелей.
Рассмотрим дифракционную картину, даваемую решеткой. Картина дифракционных максимумов и минимумов, даваемых одной щелью, не зависит от положения щели, т.е. если щель переместить параллельно самой себе, то параллельно переместится и вся дифракционная картина. Поэтому, если в пластинке проделаны одинаковые параллельные щели (рис.1), то они дадут одинаковые дифракционные картины. Если на пути лучей, распространяющихся от щелей решетки, поместить линзу, а в фокальной плоскости линзы экран, то на экране в одну точку соберутся все параллельные лучи, идущие под одним и тем же углом j к нормали.
Лучи идущие под другим углом, соберутся в другой точке. Освещенность каждой точки экрана будет зависеть как от интенсивности света, даваемого каждой щелью в отдельности, так и от результата интерференции лучей, прошедших через равные щели. В тех местах, где каждая из щелей дает минимум, будет минимум и при нескольких щелях. Но в тех местах, где каждая из щелей дает свет, не обязательно будет свет и при нескольких щелях. В некоторых направлениях лучи света, прошедшие через разные щели, могут вследствие интерференции гасить друг друга и давать добавочные, к даваемым каждой щелью, минимумы. Точно также в других направлениях лучи, складываясь, могут усиливать друг друга, давать максимумы.
Обозначим на рис. 1 ширину щели АВ = а, ширину непрозрачного промежутка ВС = в. Расстояние а + в = с называют периодом решетки или постоянной решетки.
В направлении нормали лучи идут в одинаковой фазе и при сложении усилят друг друга, дадут светлую полоску, которую называют нулевым максимумом.
Возьмем лучи., распространяющиеся от щелей под некоторым углом j к нормали, и проведем линию АР перпендикулярно к направлению лучей. От этой линии до экрана лучи, распространяющиеся от щелей, будут проходить одинаковые расстояния. Но до этой линии пути, пройденные лучами, различны. Разность хода лучей, идущих от соответственных точек соседних щелей, т.е. лучей, начинающихся у тождественных точек равна:
| d = РС = АС × Sin j = с Sin j |
На рис. 1 ряд таких соответственных точек показан стрелками.
Если разность хода d равна целому числу волн, т.е. четному числу полуволн, то все лучи, идущие от одной щели, будут при сложении усиливаться лучами, идущими от соответственных точек соседних щелей и в направлении, определяемом равенством:
с Sin j = 2k 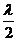 или Sin j = или Sin j = 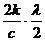 , , |
мы увидим светлую полоску, максимум. Величина k, равная любому целому числу начиная с 1, показывает порядок максимума. Из этого равенства следует, что положение максимумов не зависит от числа щелей решетки, а зависит только от длины волны падающего света и постоянной решетки.
Если разность хода d будет равна нечетному числу полуволн, то все лучи щели при сложении погасятся лучами, идущими от соответствующих точек соседних щелей. В направлении определяемом равенством
с Sin j = (2 k + 1) 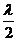 , или Sin j = , или Sin j = 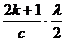 , , |
мы увидим темную полоску, добавочный минимум.
Из формулы (7) следует, что лучи различной длины волны будут иметь максимум в различных направлениях. Поэтому, если на дифракционную решетку падает белый луч, то решетка разложит его, и на экране мы увидим дифракционный спектр, обращенный к центральной полосе фиолетовой линией.
Дифракционная решетка находит большое применение в спектральном анализе, обладая рядом преимуществ по сравнению с призматическим спектрографом. Разрешающая способность спектрографов с дифракционной решеткой выше, чем у спектрографов призматических. Для определения длины волны достаточно знать период решетки и расстояние от решетки до экрана, предварительной градуировки спектрометра не требуется.
Дифракционной решеткой могут служить прозрачная жидкость или газ, в которых распространяются ультразвуковые волны. В этом случае по дифракционной картине можно определить длину ультразвуковых волн и скорость их распространения. Дифракция рентгеновских лучей при прохождении через кристалл позволяет определить структуру кристалла.
