Изменение основных термодинамических величин при сжатии реального газа

Сжатие газа — необходимый и важнейший процесс холодиль­ного цикла при использовании газообразных рабочих тел. Про­цессы сжатия реализуются в компрессорных машинах и могут протекать по-разному в машинах различных типов, характери­зоваться разной степенью необратимости. Газ можно охлаждать одновременно со сжатием или сразу после компрессора в конце­вых холодильниках.

Принципиально важно сравнить состояния сжатого и несжа­того газа при одинаковой температуре (рис.2.1.).

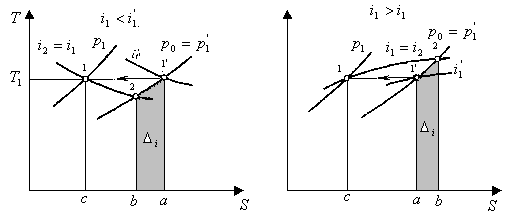Рис. 2.1. Сравнение энтальпий сжатого i₁, и несжатого i_1' реального газа при одинаковой температуре

Внутренняя энергия и энтальпия идеального газа не зависят от давления и при одинаковой температуре в состояниях 1' и 1 одинаковы . Внутренняя энергия реального газа в сжатом состоянии при одинаковой температуре всегда меньше. Физиче­ски это объясняется тем, что при сближении молекул потенци­альная составляющая внутренней энергии уменьшается.

Если внутренняя энергия реального газа при изотермическом сжатии всегда уменьшается, то характер изменения энтальпии в разных областях состояний не одинаков:

i₁— i_1' = ( u₁— u_1' ) + p₁v₁ (1 - z_1' / z₁) (2.1)

Разность u₁— u_1' в выражении (2.1) всегда отрицательна, а знак второго слагаемого определяется значениями коэффициен­тов сжимаемости z. В области состояний, где

z₁ £ z_1', энтальпия газа, как и внутренняя энергия, уменьшается при изотермическом сжатии. В области состояний, где z₁ > z_1', второе слагаемое в выражении (2.1) положительно и знак Di определя­ется соотношением абсолютных значений слагаемых, т. е. в этой области состояний энтальпия реального газа при изотермическом сжатии может и увеличиваться, и уменьшаться.

Если энтальпия сжатого газа уменьшается , то: Di = i₁– i_1'равна площади 1'ab2; теплота изотермического сжатия q _сж — площади 1'ас1, работа изотермического сжатия в открытой системе l_cж.о- площади 1'2ac1; q _сж>l_{cж. o}.

Если энтальпия сжатого газа увеличивается , то Di = i₁– i_1' равна площади 1'2ba;

q_сж— площади 1'ас1; l _{cж. о}— площади 1'2bc1; q_сж<l _{cж. о.}

Это позволяет считать, что в области состояний, где энтальпия уменьшается при изотермическом сжатии, компрессор в сово­купности со своей системой охлаждения обеспечивает создание холодопроизводительности в цикле, которая может быть реали­зована при простом адиабатном расширении газа без совершения внешней работы (например, при дросселировании). В этом случае холодопроизводительность равна разности энтальпий в состоя­ниях 1' и 1.

ДРОССЕЛИРОВАНИЕ

Адиабатное расширение газа в открытой системе в условиях стационарного течения без совершения внешней работы и прира­щения скорости на контрольной поверхности называется дроссели­рованием. Следует подчеркнуть, что стационарность течения пред­полагает в первую очередь постоянство давлений до и после дрос­селирования, а условие отсутствия приращения скорости течения на контрольной поверхности не исключает возможности ее мест­ного увеличения (или уменьшения) внутри системы, например, в самом дроссельном устройстве.

Для практического осуществления этого процесса на пути газа устанавливают какое-либо гидравлическое сопротивление: дрос­сельный вентиль, заслонку, калиброванное отверстие и пр.

Дж. Джоуль и У. Томсон исследовали этот процесс следующим образом . По медной трубке медленно протекал уста­новившийся поток газа (начальная температура T₁), проходя че­рез пробку, защищенную экранами. В опытах фиксировали изменения температуры при изменении перепада давле­ний Dр = p₁ — р_2.

Рассмот­рим элементарный объем мед­ленно текущего потока газа в двух сечениях, располо­женных по обе стороны от пробки и достаточно удален­ных от нее, где движение можно считать стационарным. Если скорости газа в рассматриваемых сечениях одинаковы, то для процесса дросселирования при l = 0 и q = 0 получим

i₂=i₁=const или u₁ + p₁v₁= u₂+ p₂v₂ = const. (2.2)

Так как никаких предположений о свойствах газов не делали, то полученный результат справедлив как для идеального, так и для реального газа: при дросселировании энтальпия газа не изменя­ется. Для идеального газа изменение внутренней энергии и эн­тальпии в любом процессе определяется выражениями du = c_v dT и di = c_p dT , откуда следует: если di = 0, то dT и du также равны нулю.

Для реального газа из уравнения (2.2) не следует постоянство температуры и внутренней энергии при дросселировании. При расширении реального газа увеличиваются расстояния между молекулами и совершается работа против молекулярных сил при­тяжения. Кроме того, в потоке реального газа работа гидродина­мических сил каждой единицы массы на входе и выходе из конт­рольной системы, равная произведению pv, различна из-за разной сжимаемости. Эти работы предопределяют изменение внутренней энергии и температуры, поэтому в общем случае для реального газа при дросселировании

di = 0 (i = const); dT ¹о; du ¹о . (2.3)

Таким образом, температура реального газа при дросселиро­вании может как понижаться, так и повышаться.

Процесс дросселирования необратим. Для идеального газа он необратим полностью, так как не сопровождается эффектами, ко­торые могли бы способствовать возвращению в исходное состояние. Приращение энтропии максимально и равно убыли энтропии при изотермическом сжатии идеального газа. Процесс дросселиро­вания реального газа частично обратим, так как сопровождается изменением температуры; при этом создается «тепловой резервуар» с температурой более высокой или более низкой и существует возможность использования перепада температур для получения работы (эту работу можно использовать для частичного возвращения газа в исходное состояние). Приращение энтропии при дросселирова­нии реального газа не равно изменению энтропии при его изо­термическом сжатии.

Определим изменение температуры реального газа при дрос­селировании

(¶Т /¶р)_i = a_i = (1/Ср) [Т (¶v/¶Т)р - v] (2.4)

Величина (¶Т/¶р)_i = a_i — дифференциальный эффект Джо­уля—Томсона, определяющий изменение температуры при беско­нечно малом падении давления в процессе дросселирования.

Практически при дросселировании всегда имеется конечная разность давлений, поэтому для такого процесса

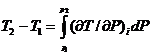(2.5)

Это выражение определяет так называемый интегральный эффект Джоуля—Томсона (изменение температуры при конечной разности давлений). Интегральный эффект дросселирования определяют обычно по таблицам или диаграммам (рис. 2.2).

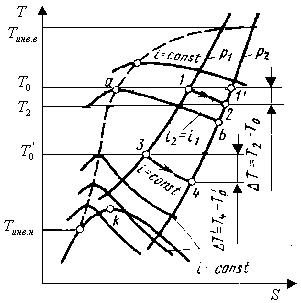Рис.2.2. Процесс дросселирования в диаграмме Т—s

Знак эффекта дроссели­рования может быть различным.

Если DТ/Dp = (T₂ — T₁)/(p₂ — p₁) > 0, то Т₂< T₁ (охлаждение), поскольку всегда p₂<p₁;

если DТ/Dр < 0, то Т₂> T₁, что соответствует нагреванию.

Из­менение знака дроссельного эффекта называют инверсией. В то­чке инверсии (¶T/¶p)_i=0. Кривая, на которой (¶T/¶p)_i=0 ,называется кривой инверсии.

Кривая инверсии разграни­чивает области положительного (охлаждение) и отрицательного (нагревание) дроссель-эффекта.

На рис. 2.3. приведены кривые инверсии для некоторых газов. Область под кривой инверсии соответствует положительному дрос­сельному эффекту.

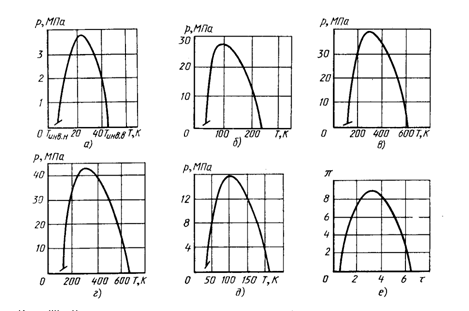
Рис. 2.3. Кривые инверсии для некоторых газов

а - гелия; б - неона; в - азота; г - воздуха; д - водорода; е - газа ван дер Ваальса

(в приведенных координатах)

Для каждого вещества сущест­вует максимальная температура инверсии Т_инв.в, выше которой при любых давлениях дроссель-эффект отрицателен. Эта темпе­ратура называется верхней температурой инверсии. Существует и так называемая нижняя температура инверсии Т_инв.н в обла­сти жидкости.

В координатах Т — s кривая инверсии проходит через экстремальные значения изоэнтальпии (i = const) и асимптотически приближается к Т_инв.в. как к тем­пературе инверсии малых давлений. Температуры инверсии для разных газов различны.

Для некоторых газов (воз­дух, азот, кислород) верхняя температура инверсии выше сред­ней температуры окружающей среды, для других (гелий, неон, водород) - ниже. Для охлаждения газа при дросселировании необходимо, прежде всего, понизить его темпера­туру до значения ниже верхней температуры инверсии Т_инв.в Если это условие выполнено, то возникает вопрос: до какого дав­ления p₁ следует сжать газ, чтобы достичь максимального инте­грального эффекта DT при известной начальной температуре T₀ (где То — обычно температура окружающей среды или тем­пература предварительного охлаждения). Продифференцировав выражение для интегрального дроссель-эффекта по

р и приравняв нулю полученное выражение, найдем

(¶Т / ¶р)_i. = 0. (2.6)

Это выражение является условием того, что искомая точка находится на кривой инверсии, а искомое давление равно давлению инверсии при данной температуре. Однако, в циклах с дросселированием практически (экономически) целесообразное давление сжатия может быть меньше давлений точки инверсии, например, в случае сжатия воздуха (при Т = 300 К ограничи­ваются давлением p » 20 МПа вместо 39 МПа). В гелиевых и водородных циклах с дросселированием оптимальные давления сжатия близки к давлениям инверсии.

При небольших давлениях значение a_i, для данного газа за­висит практически только от температуры. В области газообраз­ных состояний при снижении температуры дифференциальный эффект дрос­селирования возрастает.

При увеличении плотности газа a_i начинает зависеть от дав­ления. Экспериментально установлено, что a_i уменьшается при увеличении давления, а зависимость a_i от р близка к линейной. Влияние давления на a_i практически может сказываться только при сравнительно высоких давлениях .

Из изложенного ясно, что для увеличения интегрального эф­фекта начальную температуру процесса дросселирования следует понижать. Однако, надо четко понимать, что в низкотемпературных циклах с дросселированием холодопроизводительность теорети­ческого цикла без потерь холода не зависит от температуры начала дросселирования (процесс дросселирования в цикле не является холодопроизводящим). Увеличение интегрального эффекта дрос­селирования при снижении температуры открывает лишь прин­ципиальную возможность увеличения холодопроизводительности. Практически для этого необходимо так называемое предвари­тельное охлаждение. Роль предварительного охлаждения сво­дится к созданию теплового резервуара с температурой Т'_о, бо­лее низкой, чем температура окружающей среды T₀. При этом в области положительного дроссель-эффекта увеличивается раз­ность энтальпии сжатого и несжатого газов при одинаковой тем­пературе, что и обусловливает увеличение холодопроизводительности в цикле. Эту разность энтальпии, часто используемую при инженерных расчетах, обозначают в общем случае Di_T и называют изотермическим эффектом дросселирования. Зна­чение Di_T находят по таблицам или тепловым диаграммам как разность энтальпий сжатого и несжатого газов при данной тем­пературе.

Термины «тепловой» или «изотермический эффект дросселиро­вания» можно объяснить следующим образом. Если сравнить два состояния, соответствующие точкам 1 и 2 , то разность энтальпии i_1' – i₂, определяет количество теплоты, ко­торую можно отнять у тела, находящегося при температуре окру­жающей среды, используя эффект снижения температуры при дросселировании. С другой стороны, Di_T равна изменению энтальпии при изотермическом сжатии или расширении газа. Для того, чтобы в условиях стационарного течения расширить газ без совершения внешней работы и изменения температуры, т. е. изотермически, необходимо было бы подвести количество теплоты, равное Di_T0. При положительном дроссель эффекте Di_T опреде­ляет вклад компрессора в холодо-производительность цикла.

2.4. ПРОЦЕСС U = CONST

Если процесс расширения газа осуществить при тех же усло­виях, что и процесс дросселирования (без теплообмена с окру­жающими телами и без совершения внешней работы ), но в отличие от дросселирования расширять газ в закрытой системе, т. е. не в условиях стационарного течения, а в устройстве с жесткими стенками, то полная внутренняя энергия газа в такой системе будет постоянна. Это процесс расширения u= const; какого-либо характерного названия он не имеет. Схема реализации процесса u = const воспроизводит схему опыта Джоуля—Гей-Люссака (рис. 2.4).

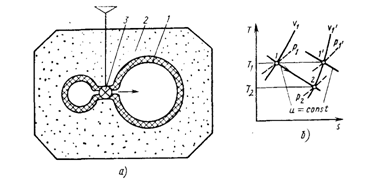
Рис.2.4. Схема реализации процесса u = const (а) и его изображение в диаграмме T—S (б)

Исследуемая система 1 состоит из двух сосудов с жест­кими стенками. Сосуды контактируют один с другим и изолиро­ваны от окружающей среды слоем изоляции 2. Начальные дав­ления газа в сосудах различные, а температуры газа одинаковые; начальное стационарное состояние с температурой T₁. При по­мощи вентиля 3 можно выравнивать давления газа в сосудах. При выпуске газа из одного сосуда давление и температура в нем снижаются; в это время в другом сосуде при втекании в него газа давление и температура повышаются. После выравнивания дав­лений в течение некоторого времени происходит выравнивание температур газа, пока система не придет в стационарное состояние с температурой Т₂. Изменение температуры газа в процессе u = const можно определить из уравнения

a_u = ( ¶T/ ¶p )_u=- (¶u / ¶р)_T / ( ¶u / ¶T )_p (2.7)

Для идеального газа ( ¶u / ¶v )_T= (¶u / ¶р)_T = 0, поэтому и dT = 0 в процессе u = const. Этот результат, установленный в опытах Джоуля—Гей-Люссака при расширении газов в области малых давлений еще в 1807 г., явился доказательством фунда­ментального положения о том, что внутренняя энергия идеального газа есть функция только температуры и не зависит от давления (плотности).

Однако, если этот опыт провести при расширении сильно сжа­тых газов, то температура не будет постоянной, а снизится: T₂< T₁. Таким об­разом, в процессе u = const для любого реального газа a_u — всегда положительная величина, т. е. температура снижается.

Процесс u = const не имеет столь большого практического значения, как процесс дросселирования i = const, однако, при­веденные соображения позволяют глубже понять сущность про­цессов внешне адиабатного расширения газа без совершения внеш­ней работы в условиях открытых и закрытых систем.