Основы атомной физики и квантовой механики
АТОМНАЯ ФИЗИКА
Методические указания
к выполнению контрольной работы № 5
для студентов – заочников
инженерно – технических специальностей
Архангельск
Рассмотрены и рекомендованы к изданию методической комиссией
факультета промышленной энергетики
Архангельского государственного технического университета
29 ноября 2006 года
Составитель:
А.И. Аникин, доц., канд. техн. наук
Рецензент
А.В. Соловьев, доц., канд. техн. наук
УДК 539.1
Аникин А.И. Атомная физика: Методические указания к выполнению контрольной работы № 5 для студентов-заочников инженерно-технических специальностей. – Архангельск: Изд-во АГТУ, 2007. – 38 с.
Подготовлены кафедрой физики АГТУ.
В методических указаниях приведены основные формулы по атомной физике, примеры решения задач, варианты контрольных заданий, а также необходимый справочный материал.
Предназначены для студентов-заочников инженерно-технических специальностей.
Ил. 5. Табл. 8. Библиогр. 5 назв.
© Архангельский государственный
технический университет, 2007
© А.И.Аникин, 2007
ВВЕДЕНИЕ
Контрольные работы по физике предусматривают решение задач и помогают закрепить усвоение теоретической части курса. Чтобы научиться решать задачи и подготовиться к выполнению контрольной работы, следует разобрать помещенные в настоящем пособии примеры решения задач с подробными пояснениями, а также самостоятельно решить ряд задач из задачников по физике.
При решении задач следует руководствоваться такими правилами.
1. Внимательно прочитать условие задачи, уяснить, какой физический процесс или явление в ней рассматриваются.
2. Записать условие задачи в сокращенном виде, применяя обще-принятые обозначения физических величин. При решении задач следует пользоваться Международной системой единиц (СИ). Все числовые величины должны быть приведены к этой системе. Следует проанализировать, все ли данные, необходимые для решения задачи, приведены в условии. Недостающие данные надо взять из справочных таблиц. Необходимо записывать также и те величины, числовые значения которых не задаются, но о них можно судить по условию задачи. Например, если тело начинает двигаться из состояния покоя, то следует записать, что начальная скорость
υ0 = 0, если в задаче сказано, что какой-то величиной x можно пренебречь, обязательно следует записать, что x = 0 и т. д.
3. Задачу следует обязательно пояснять чертежом или рисунком (если это возможно), выполняя их аккуратно с помощью чертежных принадлежностей. Обозначения на чертеже и в решении должны быть одинаковыми. Не следует обозначать одну и ту же величину разными буквами, а также обозначать различные величины одними и теми же символами.
4. Решение задачи должно сопровождаться пояснениями. В пояснениях необходимо указывать те основные законы и формулы, на которых базируется решение задачи.
5. Как правило, задача по физике решается сначала в общем виде, то есть выводится формула, в которой искомая величина выражена через ве-личины, заданные в условии задачи. При таком решении не происходит накопления погрешностей, неизбежных при промежуточных расчетах.
6. Получив решение в общем виде, сделать анализ его размерности. Для этого подставить в правую часть полученной рабочей формулы вместо символов величин обозначения единиц измерений, провести с ними необходимые действия и убедиться в том, что полученная при этом единица соответствует искомой величине.
7. Произвести вычисления путем подстановки заданных числовых величин в расчетную формулу. Все вычисления рекомендуется выполнять с помощью микрокалькулятора. При вычислениях соблюдать правила приближенных вычислений и округлений.
8. Оценить правдоподобность ответа. Такая оценка в ряде случаев позволяет обнаружить ошибочность ответа.
9. Ответ должен быть записан с определенной степенью точности, соответствующей точности исходных данных.
КОНТРОЛЬНАЯ РАБОТА № 5
Контрольная работа включает решение восьми задач. Вариант контрольной работы выбирается по последней цифре шифра студента, номера задач – по таблице. Справочные данные, необходимые при решении задач, приведены в приложении.
Таблица
Варианты контрольной работы
| Вариант | Номера задач | |||||||
1. Атом водорода в основном состоянии поглотил квант света с длиной волны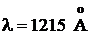 
. Определить радиус электронной орбиты возбужденного атома водорода.
2. Какую работу следует совершить, чтобы удалить электрон со второй орбиты атома водорода за пределы притяжения электрона ядром?
3. Определить частоту света, излучаемого ионом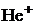 
при переходе его на энергетический уровень с главным квантовым числом 
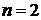, если радиус орбиты электрона при этом уменьшился в 9 раз.
4. Найти период Т обращения электрона на первой боровской орбите атома водорода и его угловую скорость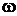 
.
5. На какой орбите скорость электрона в атоме водорода равна
734 км/с?
6. Фотон, соответствующий длине волны 0,020 мкм, выбил электрон из невозбужденного атома водорода. Вычислить скорость электрона за пределами атома.
7. Во сколько раз увеличится радиус орбиты электрона у атома водорода, находящегося в основном состоянии, при возбуждении его фотоном с энергией 12,09 эВ?
8. У какого водородоподобного иона разность длин волн первых линий серий Бальмера и Лаймана равна 59,3 нм?
9. Покоившийся атом водорода испустил фотон, соответствующий первой линии серии Лаймана. Какую скорость приобрел атом?
10. При переходе электрона в атоме водорода из возбужденного состояния в основное радиус орбиты электрона уменьшился в 16 раз. Определить длину волны излученного фотона.
11. Заряженная частица, ускоренная разностью потенциалов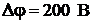 
, имеет длину волны де Бройля 
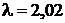пм. Найти массу частицы m, если ее заряд численно равен заряду электрона.
12. Параллельный пучок электронов, прошедших ускоряющую разность потенциалов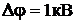 
, падает на щель шириной 
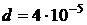м. Определить ширину 
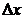изображения щели на люминесцентном экране, находящемся на расстоянии 
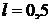м от щели. За ширину изображения щели принять расстояние между дифракционными минимумами первого порядка.
13. Какую энергию необходимо дополнительно сообщить электрону, чтобы его дебройлевская длина волны уменьшилась от 100 до 50 пм?
14. Вычислить длину волны де Бройля для молекулы серебра (Аg), движущейся со скоростью, совпадающей со средней квадратической скоростью молекул при температуре 27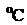 
. Будет ли испытывать эта молекула дифракцию при прохождении через щель шириной 1 мм?
15. Протон обладает кинетической энергией 1 кэВ. Определить величину дополнительной энергии, которую необходимо ему сообщить для того, чтобы дебройлевская длина волны уменьшилась в три раза.
16. Электрон движется по окружности радиусом 0,5 см в однородном магнитном поле с индукцией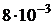 
Тл. Определить длину волны де Бройля электрона.
17. Какую ускоряющую разность потенциалов должен пройти электрон, чтобы длина волны де Бройля была равна 1,0 нм?
18. Вычислить длину волны де Бройля для электрона, движущегося по круговой орбите атома водорода, находящегося в основном состоянии.
19. Параллельный поток электронов, движущихся с одинаковой скоростью, падает нормально на диафрагму с узкой прямоугольной щелью шириной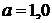 
мкм. Определить скорость этих электронов, если на экране, отстоящем от щели на расстоянии 
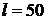см, ширина центрального дифракционного максимума 
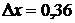мм.
20. Вычислить длину волны де Бройля протона, прошедшего ускоряющую разность потенциало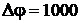в 
В.
21. Используя соотношение неопределенностей, оценить ошибки в определении скоростей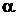 
-частицы и шарика массой 0,1 мг, если координаты центров масс этих частиц могут быть установлены с неопределенностью 10 мкм.
22. Найти неопределенность в определении координаты электрона, движущегося в атоме водорода со скоростью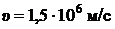 
, если допускаемая неточность 
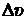в определении скорости составляет 10% от ее величины. Сравнить полученную неточность с диаметром атома водорода, вычисленным по теории Бора для основного состояния, и указать, применимо ли понятие траектории в данном случае.
23. Электрон с кинетической энергией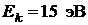 
находится в металлической пылинке диаметром 
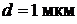. Оценить (в процентах) относительную неточность 
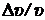, с которой может быть определена скорость электрона.
24. Среднее время жизни атома в возбужденном состоянии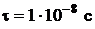 
. При переходе в основное состояние атом испустил фотон с длиной волны 
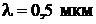. Оценить энергию фотона и неопределенность его длины волны.
25. Диаметр пузырька в жидководородной пузырьковой камере составляет величину порядка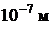 
. Рассчитать неопределенность в определении скоростей электрона и 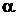-частицы в такой камере, если неопределенность в определении координаты принять равной диаметру пузырька.
26. Оценить с помощью соотношения неопределенностей минимальную кинетическую энергию электрона, движущегося в области пространства размером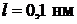 
.
27. Оценить наименьшие ошибки, с которыми можно определить скорости электрона, протона и шарика массой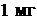 
, если координаты частиц и центра тяжести шарика установлены с неопределенностью 
.
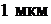28. Альфа-частица находится в бесконечно глубокой одномерной прямоугольной «потенциальной яме». Используя соотношение неопределенностей, найти ширину «ямы»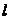 
, если известна минимальная энергия
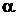-частицы 
.
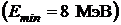29. Ширина следа электрона по фотографии, полученной с помощью камеры Вильсона, составляет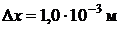 
. Найти неопределенность в определении скорости электрона, если неопределенность в определении координаты принять равной ширине следа на фотографии.
30. В некоторый момент времени область локализации свободного электрона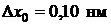 
. Оценить ширину области локализации этого электрона спустя промежуток времени 
.
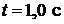31. Электрон находится в одномерной прямоугольной «потенциальной яме» с бесконечно высокими «стенками». Найти ширину «ямы», если разность энергии между уровнями с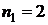 
и 
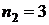составляет 
.
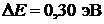32. Электрон в одномерной прямоугольной «потенциальной яме» шириной 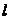находится в возбужденном состоянии 
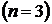. Определить, в каких точках интервала 
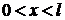плотность вероятности нахождения электрона равна 0. Найти вероятность пребывания электрона в области 
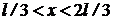. Решение пояснить графиком.
33. Пси-функция основного состояния атома водорода имеет вид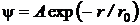 
, где А – некоторая постоянная, 
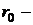радиус первой боровской орбиты. Определить наиболее вероятное расстояние 
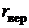электрона от ядра.
34. Частица находится в основном состоянии в одномерной прямоугольной «потенциальной яме» шириной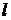 
с абсолютно непроницаемыми «стенками». Найти вероятность пребывания частицы в области .
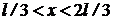35. Какова ширина 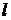одномерной «потенциальной ямы» с бесконечно высокими «стенками», если при переходе электрона со второго квантового уровня на первый излучается энергия 1 эВ? Как изменится излучаемая энергия, если 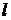увеличится в 10 раз?
36. Частица в одномерной «потенциальной яме» шириной 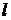находится в возбужденном состоянии 
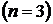. Определить, в каких точках в интервале 
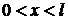плотность вероятности нахождения частицы имеет минимальное и максимальное значения. Решение задачи пояснить рисунком.
37. Электрон находится в одномерной прямоугольной «потенциальной яме» с бесконечно высокими «стенками». Ширина «ямы»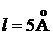 
. Определить наименьшую разность 
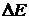энергетических уровней электрона. Ответ выразить в электрон-вольтах.
38. Волновая функция, описывающая движение электрона в основном состоянии атома водорода, имеет вид 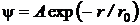, где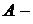 
некоторая постоянная, 
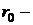радиус первой боровской орбиты. Вычислить вероятность того, что электрон в атоме водорода находится от ядра на расстоянии, превышающем 
.
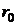39. Электрон находится в одномерной прямоугольной «потенциальной яме» с бесконечно высокими «стенками». Ширина «ямы»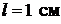 
. В каких точках в интервале 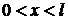плотность вероятности нахождения электрона на первом и втором энергетических уровнях одинакова? Вычислить плотность вероятности для этих точек. Решение задачи пояснить рисунком.
40. Частица находится в одномерной прямоугольной «потенциальной яме» с бесконечно высокими «стенками». Найти массу частицы, если ширина ямы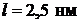 
, а разность энергий 3-го и 2-го энергетических уровней 
.
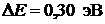41. Определить уровень Ферми при абсолютном нуле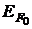 
для меди, полагая, что на каждый атом меди приходится один свободный электрон.
42. Во сколько раз увеличится при повышении температуры от 300 до 350 К электропроводность собственного полупроводника, ширина запрещенной зоны которого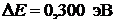 
?
43. Найти число свободных электронов, приходящихся на один атом натрия при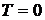 
K, если уровень Ферми для натрия 
.
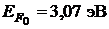44. Металл находится при температуре 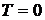К. Определить, во сколько раз число электронов со скоростями от 
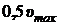до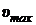 
больше числа электронов со скоростями от 0 до .
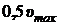45. При нагревании полупроводника, обладающего собственной проводимостью, от температуры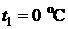 
до температуры 
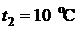его сопротивление уменьшается в 2,28 раза. Определить ширину запрещенной зоны полупроводника.
46. Во сколько раз число свободных электронов, приходящихся на один атом металла при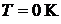 
, больше в алюминии, чем в меди, если уровни Ферми соответственно равны 
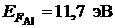и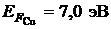 
?
47. Определить долю свободных электронов в металле при температуре Т = 0 К, энергии Е которых заключены в интервале значений от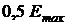 
до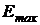 
.
48. Найти температуру вырождения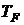 
, выше которой квантовые эффекты перестают быть существенными для калия, если принять, что на каждый атом приходится по одному свободному электрону.
49. Найти минимальную энергию образования пары электрон – дырка в чистом беспримесном полупроводнике, удельная электрическая проводимость которого возрастает в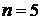 
раз при увеличении температуры от 
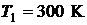до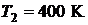 
.
50. Полагая, что на каждый атом алюминия в кристалле приходится по три свободных электрона, определить максимальную энергию 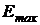электронов при температуре 
.
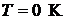51. Найти постоянную распада и среднее время жизни радиоактивного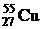 
, если известно, что его активность уменьшается на 4,0% за час. Продукт распада нерадиоактивен.
52. Какая доля радиоактивных ядер, период полураспада которых 71,3 дня, распадается за месяц?
53. Определить возраст древних деревянных предметов, если известно, что удельная активность изотопа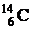 
в них составляет 3/5 удельной активности этого изотопа в только что срубленных деревьях. Период полураспада ядер 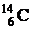равен 5570 лет.
54. Активность некоторого радиоактивного вещества уменьшается в 2,5 раза за 7,0 суток. Найти период полураспада этого вещества.
55. Некоторый радиоактивный изотоп имеет постоянную распада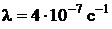 
. Через какое время 
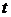распадается 75% первоначальной массы атомов 
?
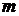56. Из каждого миллиона атомов радиоактивного изотопа каждую секунду распадается 200 атомов. Определить период полураспада этого вещества.
57. В кровь человека ввели небольшое количество раствора, содержащего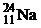 
с активностью 
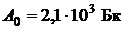. Активность 1 см3 крови, взятой через 
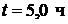после этого, оказалась равной 
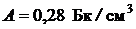. Найти объем крови человека.
58. Счетчик Гейгера, установленный вблизи препарата радиоактивного изотопа серебра, регистрирует поток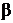 
- частиц. При первом измерении поток Ф1 частиц был равен 
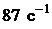, а по истечении суток поток Ф2 оказался равным 
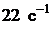. Определить период полураспада этого изотопа.
59. За один год начальное количество радиоактивного изотопа уменьшилось в три раза. Во сколько раз оно уменьшится за два года?
60. Найти активность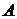 
массы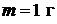 
радия, период полураспада которого 1620 лет.
61. Сколько теплоты выделяется при образовании одного грамма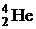 
из дейтерия 
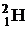? Какая масса каменного угля с удельной теплотой сгорания 30 кДж/г эквивалентна в тепловом отношении полученной величине?
62. Атомное ядро, поглотившее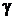 
- фотон с длиной волны 
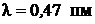, пришло в возбужденное состояние и распалось на отдельные нуклоны, разлетевшиеся в разные стороны. Суммарная кинетическая энергия нуклонов 
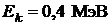. Определить энергию связи 
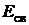ядра.
63. При взрыве водородной бомбы протекает термоядерная реакция образования гелия из дейтерия и трития. Написать уравнение реакции. Найти энергию Q, выделяющуюся при этой реакции. Какую энергию можно получить при образовании 1 г гелия?
64. Найти среднюю энергию связи на один нуклон в ядре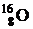 
.
65. Считая, что в одном акте деления ядра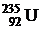 
освобождается энергия 200 МэВ, определить энергию, выделяющуюся при сгорании одного килограмма изотопа 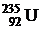, и массу каменного угля с удельной теплотой сгорания 30 кДж/г, эквивалентную в тепловом отношении одному килограмму .
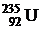66. При бомбардировке изотопа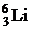 
дейтронами образуются две
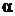- частицы, при этом выделяется энергия 
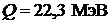. Зная массы дейтрона и 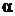- частицы, найти массу изотопа 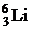(в а.е.м.).
67. Найти энергию связи ядер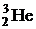 
и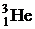 
. Какое из этих ядер более устойчиво?
68. Найти минимальную энергию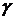 
- кванта, достаточную для осуществления реакции разложения первоначально покоившегося дейтрона 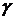- лучами: 
.
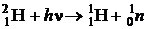69. Определить суммарную кинетическую энергию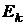 
ядер, образовавшихся в результате реакции 
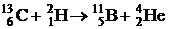. Кинетическая энергия дейтрона 
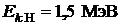. Ядро-мишень 
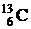считать неподвижным.
70. Найти энергию ядерной реакции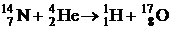 
. Освобождается или поглощается энергия при этой реакции?
71. Остановившийся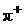 
- мезон распался на мюон и нейтрино. Найти кинетическую энергию мюона и нейтрино.
72. Найти средний путь, проходимый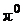 
- мезонами, кинетическая энергия которых в 
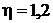раза превышает их энергию покоя. Среднее время жизни очень медленных 
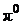- мезонов 
.
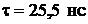73. Позитрон с кинетической энергией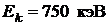 
налетает на покоящийся свободный электрон. В результате аннигиляции возникают два 
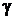- кванта с одинаковыми энергиями. Определить угол между направлениями их разлета.
74. Ядро изотопа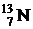 
выбросило позитрон с кинетической энергией 1 МэВ. Пренебрегая кинетической энергией ядра отдачи, определить кинетическую энергию нейтрино, выброшенного вместе с позитроном.
75. Фотон с энергией 3 МэВ превратился в пару электрон-позитрон. Принимая, что кинетическая энергия частиц одинакова, определить кинетическую энергию каждой частицы.
76. Покоящийся нейтрон распадается по схеме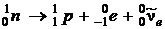 
. Определить суммарную кинетическую энергию всех частиц, возникающих в процессе распада нейтрона. Массой покоя антинейтрино пренебречь.
77. Отрицательно заряженный мюон испытывает упругое лобовое столкновение с покоящимся электроном. Найти кинетическую энергию электрона отдачи, если кинетическая энергия мюона до столкновения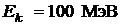 
.
78. Отрицательные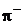 
- мезоны с кинетической энергией 
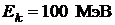пролетают от места рождения до распада в среднем расстояние 
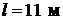. Найти собственное время жизни этих мезонов.
79. Нейтрон и антинейтрон соединяются, образуя два одинаковых фотона. Найти энергию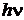 
каждого из фотонов, считая, что начальная кинетическая энергия частиц ничтожно мала.
80. Альфа-частица с кинетической энергией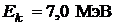 
испытала упругое соударение с первоначально покоившимся ядром 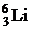. Какую кинетическую энергию получило ядро 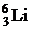, если угол между направлениями разлета обеих частиц 
?
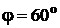ПРИЛОЖЕНИЕ
Таблица 1
Некоторые физические постоянные (округленные значения)
| Физическая постоянная | Обозна- чение | Числовое значение | Единица измерения |
| Скорость света в вакууме Постоянная Планка Постоянная Больцмана Постоянная Авогадро Молярная газовая постоянная Постоянная Ридберга Электрическая постоянная Элементарный электрический заряд Радиус первой боровской орбиты | с h k NA R0 R 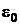 е r0 | 3,000∙10 8 6,626∙10 – 34 1,381∙10 – 23 6,022∙10 23 8,314 1,097∙10 7 8,854∙10 – 12 1,602∙10 – 19 0,529∙10 – 10 | м/с Дж∙с Дж/К моль – 1 Дж/(моль∙К) м – 1 Ф/м Кл м |
Таблица 2
Массы покоя некоторых частиц
| Частица | Масса | |
| а. е. м. | кг | |
| Электрон Протон Нейтрон Дейтрон Альфа–частица Положительный π+ - мезон Отрицательный π – - мезон Нейтральный π0 - мезон Нейтрино Мюон | 5,48580∙10 – 4 1,00728 1,00867 2,01354 4,00149 0,1498 0,1498 0,1449 0,1134 | 9,10953∙10 – 31 1,67265∙10 – 27 1,67495∙10 – 27 3,34362∙10 – 27 6,64473∙10 – 27 2,488∙10 – 28 2,488∙10 – 28 2,406∙10 – 28 1,884∙10 – 28 |
Таблица 3
Массы некоторых нейтральных атомов
| Изотоп | Масса | |
| а. е. м. | кг | |
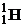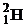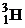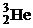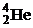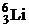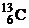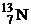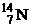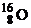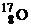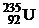             | 1,00783 2,01410 3,01605 3,01603 4,00260 6,01512 13,0033 13,0057 14,0031 15,9949 16,9991 26,9815 235,044 | 1,67357∙10 – 27 3,34454∙10 – 27 5,00835∙10 – 27 5,00832∙10 – 27 6,64658∙10 – 27 9,98850∙10 –27 2,15929∙10 – 26 2,15969∙10 – 26 2,32530∙10 – 26 2,65606∙10 – 26 2,82282∙10 – 26 4,48047∙10 – 26 3,90306∙10 – 25 |
Таблица 4
Плотности некоторых твердых тел
| Твердое тело | Плотность, кг/м3 |
| Алюминий Калий Медь Натрий | 2,70∙10 3 0,87∙10 3 8,93∙10 3 0,97∙10 3 |
Таблица 5
Коэффициенты перевода некоторых внесистемных единиц в единицы СИ
| Величина | Соотношение с единицами СИ |
| Длина Масса Энергия |    |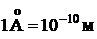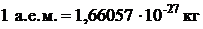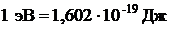
Таблица 6
Некоторые постоянные числа и математические формулы
| Постоянные числа | Математические формулы |
е = 2,7183 π = 3,1416  |    |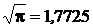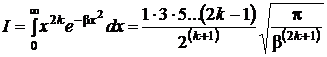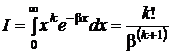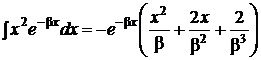
Примечание. В таблице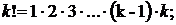 
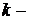любое целое число; 
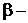константа 
.
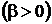Таблица 7
Множители и приставки для образования кратных
и дольных единиц системы СИ и их наименования
| Приставка | Множитель | Обозначение приставки |
| пико нано микро милли кило мега | 10 – 12 10 – 9 10 – 6 10 – 3 10 3 10 6 | п н мк м к М |
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Курс физики [Текст]: Учебник для вузов / Под ред. В.Н.Лозовского –
4 - е изд., стереотипное – СПб.: Лань, 2006. Т.1-2.
2. Савельев И.В. Курс общей физики [Текст]: Учеб. пособие для втузов / И.В.Савельев – М.: Астрель; АСТ, 2001. Т.1-5.
3. Трофимова Т.И. Курс физики [Текст]: Учеб. пособие для вузов / Т.И.Трофимова – 7 - е изд., стереотипное – М.: Высш. шк., 2002. – 542 с.
4. Чертов А.Г. Задачник по физике [Текст]: Учеб. пособие для втузов / А.Г.Чертов, А.А.Воробьев – 7 - е изд., перераб. и доп. – М.: Изд-во
физ.-мат. литературы, 2003. – 640 с.
5. СТО АГТУ 01.04 – 2005. Работы студентов. Общие требования и правила оформления [Текст]. – Введ. 11.01.2006. – Архангельск: Изд-во Архан. гос. техн. ун-та, 2006. – 104 с.
ОГЛАВЛЕНИЕ
Введение ………………………………………………………...……………3
Основы атомной физики и квантовой механики .……………...…………..4
Элементы квантовой статистики и физики твердого тела …….………...15
Физика атомного ядра и элементарных частиц …………………………..18
Порядок выполнения контрольной работы ………………………………25
Контрольная работа № 5 …………………………………………………...26
Приложение …………………………………………………………………34
Библиографический список ………………………………………...………..36
Андрей Иванович Аникин
АТОМНАЯ ФИЗИКА
Методические указания
к выполнению контрольной работы № 5
для студентов-заочников
инженерно-технических специальностей
Компьютерный набор И.М.Филиной
АТОМНАЯ ФИЗИКА
Методические указания
к выполнению контрольной работы № 5
для студентов – заочников
инженерно – технических специальностей
Архангельск
Рассмотрены и рекомендованы к изданию методической комиссией
факультета промышленной энергетики
Архангельского государственного технического университета
29 ноября 2006 года
Составитель:
А.И. Аникин, доц., канд. техн. наук
Рецензент
А.В. Соловьев, доц., канд. техн. наук
УДК 539.1
Аникин А.И. Атомная физика: Методические указания к выполнению контрольной работы № 5 для студентов-заочников инженерно-технических специальностей. – Архангельск: Изд-во АГТУ, 2007. – 38 с.
Подготовлены кафедрой физики АГТУ.
В методических указаниях приведены основные формулы по атомной физике, примеры решения задач, варианты контрольных заданий, а также необходимый справочный материал.
Предназначены для студентов-заочников инженерно-технических специальностей.
Ил. 5. Табл. 8. Библиогр. 5 назв.
© Архангельский государственный
технический университет, 2007
© А.И.Аникин, 2007
ВВЕДЕНИЕ
Контрольные работы по физике предусматривают решение задач и помогают закрепить усвоение теоретической части курса. Чтобы научиться решать задачи и подготовиться к выполнению контрольной работы, следует разобрать помещенные в настоящем пособии примеры решения задач с подробными пояснениями, а также самостоятельно решить ряд задач из задачников по физике.
При решении задач следует руководствоваться такими правилами.
1. Внимательно прочитать условие задачи, уяснить, какой физический процесс или явление в ней рассматриваются.
2. Записать условие задачи в сокращенном виде, применяя обще-принятые обозначения физических величин. При решении задач следует пользоваться Международной системой единиц (СИ). Все числовые величины должны быть приведены к этой системе. Следует проанализировать, все ли данные, необходимые для решения задачи, приведены в условии. Недостающие данные надо взять из справочных таблиц. Необходимо записывать также и те величины, числовые значения которых не задаются, но о них можно судить по условию задачи. Например, если тело начинает двигаться из состояния покоя, то следует записать, что начальная скорость
υ0 = 0, если в задаче сказано, что какой-то величиной x можно пренебречь, обязательно следует записать, что x = 0 и т. д.
3. Задачу следует обязательно пояснять чертежом или рисунком (если это возможно), выполняя их аккуратно с помощью чертежных принадлежностей. Обозначения на чертеже и в решении должны быть одинаковыми. Не следует обозначать одну и ту же величину разными буквами, а также обозначать различные величины одними и теми же символами.
4. Решение задачи должно сопровождаться пояснениями. В пояснениях необходимо указывать те основные законы и формулы, на которых базируется решение задачи.
5. Как правило, задача по физике решается сначала в общем виде, то есть выводится формула, в которой искомая величина выражена через ве-личины, заданные в условии задачи. При таком решении не происходит накопления погрешностей, неизбежных при промежуточных расчетах.
6. Получив решение в общем виде, сделать анализ его размерности. Для этого подставить в правую часть полученной рабочей формулы вместо символов величин обозначения единиц измерений, провести с ними необходимые действия и убедиться в том, что полученная при этом единица соответствует искомой величине.
7. Произвести вычисления путем подстановки заданных числовых величин в расчетную формулу. Все вычисления рекомендуется выполнять с помощью микрокалькулятора. При вычислениях соблюдать правила приближенных вычислений и округлений.
8. Оценить правдоподобность ответа. Такая оценка в ряде случаев позволяет обнаружить ошибочность ответа.
9. Ответ должен быть записан с определенной степенью точности, соответствующей точности исходных данных.
ОСНОВЫ АТОМНОЙ ФИЗИКИ И КВАНТОВОЙ МЕХАНИКИ
1. Обобщенная формула Бальмера для атома водорода
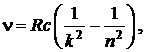
где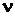 
– частота излучения, соответс