Б17. 1) Принцип суперпозиции и его применение к расчёту поля системы неподвижных зарядов.

Вектор напряжённости поля, создаваемого системой неподвижных точечных зарядов, равен векторной сумме напряжённостей полей, создаваемых каждым из зарядов в отдельности: 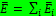. Это следует из того, что силы складываются как векторы: , поэтому

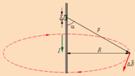
Поле равномерно заряженного кольца.

Воспользуемся принципом суперпозиции. Разобьём кольцо на элементы – точечные заряды q, каждый из которых создает в точке А напряженность 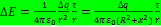Вследствие симметрии, вклад в общую напряженность дадут лишь вертикальные составляющие Е. Поэтому напряженность в точке А будет определятся только суммой Е по всем элементам кольца:

Принцип суперпозиции магнитных полей.

Если магнитное поле создано несколькими проводниками с токами, то вектор магнитной индукции в какой-либо точке этого поля равен векторной сумме магнитных индукций, созданных в этой точке каждым током в отдельности: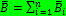

Поле прямого тока.создается током, текущего по тонкому прямому бесконечному проводу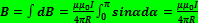

Б18. 1) Электроёмкость проводников и конденсаторов.

Емкость конденсатора: ; Емкость уединенного проводника: ; Шар R: 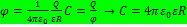. Плоский: . Цилиндрический: Сферический:

Вычисление ёмкости сферического конденсатора.

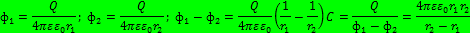
Теорема о циркуляции вектора напряженности магнитного поля в интегральной и дифференциальной формах.

Б19.1) Электростатическое поле вблизи поверхности проводника.

Напряженность поля вблизи поверхности заряженного проводника прямопропорциональна поверхностной плотности зарядов.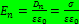

Магнитное давление.

Вычислим давление магнитного поля. Объёмная плотность силы – плотность тока в лое. Давление получается интегрированием по х. Плотность тока исключим, используя уравнение 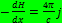. В результате имеем 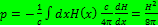Таким образом давление магнитного поля равно плотности его энергии.

Б20.1) Электрический ток.

Упорядоченное движение заряженных частиц в проводнике. Чтобы он возник, следует предварительно создать электрическое поле.

Уравнение непрерывности.

В интегральной форме . В дифференциальной форме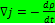

Контур с током в магнитном поле. Сила, действующая на контур с током в магнитном поле.

Рассмотрим прямоугольный контур с током I стороны которого составляют a и b, помещенный в магнитное поле В. Силы: 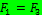= IaBsin90=IaB. Сумма всех сил равна 0, но суммарный момент сил 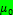не равен 0. Таким образом, контур будет проворачиваться относительно неподвижного центра масс

Запишем моменты сил относительно оси z, которая проходит через центр контура: Моменты сил F2 и F4 =0, момент сил F1 и F3 равны друг другу и составляют 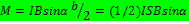, где S=ab – площадь контура.

Отсюда, суммарный момент сил: 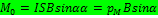; 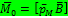Момент 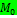поворачивает контур до тех пор, пока направление магнитного момента 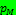не совпадает с направлением поля В.

Б21.1) Плотность энергии электростатического поля.

, V объём конденсатора. Разделим выражение на V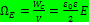

Сила Лоренца.

Сила, действующая на эл. заряд Q. F=Q[vB]. Направление по правилу левой руки. Если на движущийся заряд помимо магн. поля действует эл. Поле, то сила равна векторной сумме сил. F=qE+q[VxB].