Интерференция и дифракция света
В этих явлениях проявляется волновая природа света. Интересно, что волновая теория света была разработана значительно раньше, чем стала известна электромагнитная природа света.
Интерференция. Интерференцией называется перераспределение интенсивности света в пространстве при наложении световых волн друг на друга. Необходимым условием интерференции воли является юс когерентность. Под когерентностью понимается согласованное в пространстве и времени протекание волновых процессов. Строго когерентны лишь монохроматические волны одинаковой частоты. Рассмотрим две когерентные световые волны:
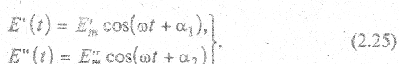
здесь α1 и α2 - начальные фазы вонл.
Предположим для простоты, что амплитуды волн равны:
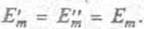 |
Результатом наложения волн (2.25) является волна
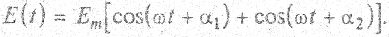
Распишем выражение в квадратных скобках как сумму косинусов и получим

Результирующая волна (2.26) также монохроматическая, имеет частоту со и амплитуду 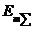 , зависящую от начальных фаз складываемых волн
, зависящую от начальных фаз складываемых волн
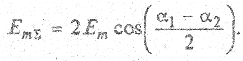
Интенсивность результирующей волны 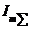
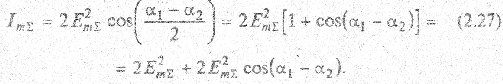
Для общего случая с различными амплитудами складываемых • волн получим
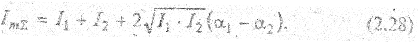
Перекрестный член в правой части (2.28) называется интерференционным. В зависимости от разности фаз складываемых волн (α1 - α2) интенсивность результирующей волны может оказаться и больше, и меньше суммы интенсивностей исходных волн. Вообще, интенсивность результирующего колебания максимальна и равна
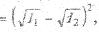
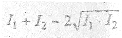
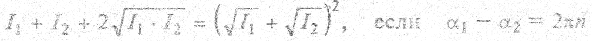
(n = 0, 1, 2, ...) и минимальна и равна
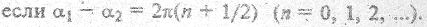
Так, при 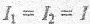 результирующая интенсивность равна нулю, если α1 – α2 = π и равна 4I, если α1 – α2 = 0.
результирующая интенсивность равна нулю, если α1 – α2 = π и равна 4I, если α1 – α2 = 0.
Все реальные электромагнитные волны не являются строго монохроматическими и строго плоскополяризованными, а следовательно, — строго когерентными.
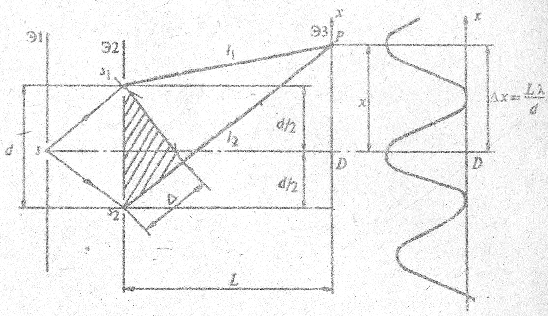 |
Рис. 2.13.
Способность реальных волн интерферировать и характеризует степень их когерентности. Относительно легко обеспечивается когерентность радиоволн. В микроволновом диапазоне источниками когерентных волн являются мазеры, а в оптическом диапазоне - лазеры. Для более высокочастотных электромагнитных волн искусственные когерентные источники пока не созданы. Естественные источники, как указывалось выше, всегда излучают некогерентные световые волны. Отсюда следует, что наблюдать интерференцию волн разных естественных источников невозможно.
Однако, если разделить свет от одного источника на две (или несколько) системы волн, оказывается, что эти системы когерентны и способны интерферировать. Это объясняется тем, что каждая система представляет излучение одних и тех же атомов источника.
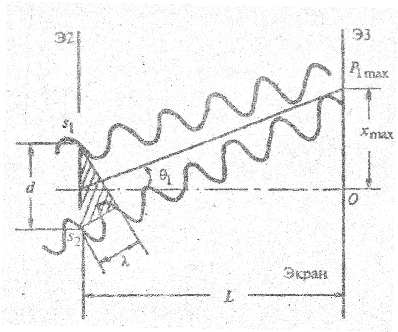 |
Рис. 2.14.
На рис. 2.13 представлена принципиальная система наблюдения интерференции света по методу Юнга. Источником света является ярко освещенная цель s в экране Э1. Свет из нее попадает на экран Э2, в котором имеются две одинаковые узкие щели s1 и s2. Щели s1 и s2 можно рассматривать как два когерентных источника.
Результат интерференции наблюдается на экране ЭЗ в виде чередующихся темных (минимумы) и светлых (максимумы) полос, параллельных друг другу.
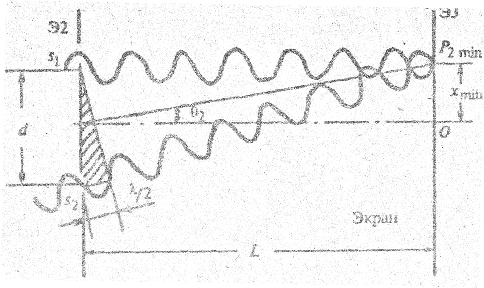
Рис. 2.15.
Конкретно результат интерференции зависит от соотношения фаз волн в данной точке экрана. Если волны приходят в фазе (рис. 2.14), они усиливают друг друга, наблюдается максимум; если в противофазе - минимум (рис. 2.15). Соотношение фаз зависит от длины волны света λ в вакууме, расстояния между целями - d, а также угла θ, под которым ведется наблюдение.
Рассмотрим результат наложения волн в некоторой точке Р, отстоящей от осевой линии на расстояние х (см. рис. 2.13).
Разность хода лучей 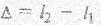 определится из соотношения
определится из соотношения
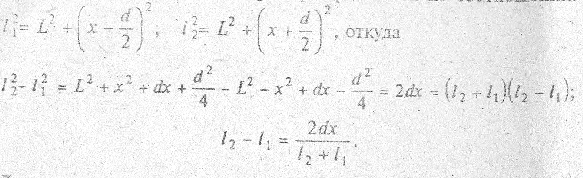
Для получения различимой интерференционной картины надо иметь 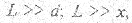 следовательно, можно принять
следовательно, можно принять 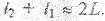

С другой стороны, 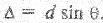 . Из рис. 2.14 следует, что если на разности хода укладывается целое число длин волн λ, то в тогчку наблюдения Р1 волны приходят в фазе, усиливают друг друга, что соответствует максимуму. Условие интерференционных максимумов
. Из рис. 2.14 следует, что если на разности хода укладывается целое число длин волн λ, то в тогчку наблюдения Р1 волны приходят в фазе, усиливают друг друга, что соответствует максимуму. Условие интерференционных максимумов
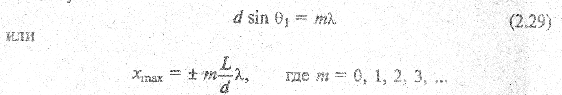
Если же на разности хода укладывается полуцелое число длин волн, в точку наблюдения Р2 они приходят в противофазе, гасят друг друга, что соответствует минимуму (см. рис. 2.15).
Условие интерференционных минимумов
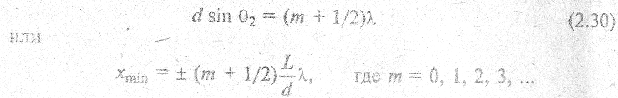 |
В центре экрана 33 (т.О) будет наблюдаться центральный - максимум — максимум нулевого порядка. Знаки «±» соответствуют расположению максимумов и минимумов по обе стороны симметрично от центрального максимума. Число m определяет порядок интерференционных максимумов и минимумов. Расстояние между двумя соседними максимумами (или минимумами) называется шириной интерференционной полосы ∆х. Оно равно 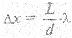 и постоянно для данного опыта.
и постоянно для данного опыта.
Дифракция света. Если свет распространяется в однородной области пространства, и длина световой волны, пренебрежимо мала по сравнению с характеристическими размерами области, то распространение света подчиняется законам геометрической оптики. В этом случае пользуются понятием светового луча, т.е. весьма узкого пучка света, распространяющегося прямолинейно. В том же случае, если в области распространения имеются резкие оптические неоднородности (отверстия, препятствия, границы непрозрачных тел и т. п.), размер которых сравним с длиной волны света, возникает дифракция — огибание световыми волнами .препятствий, проникновение в область геометрической тени, т.е. отклонение от законов геометрической оптики.
По физическому смыслу дифракция не отличается от интерференции. Оба эти явления связаны с перераспределением интенсивности светового потока в результате наложения когерентных волн. Рассчитывать распределение света в результате дифракции - дифракционную картину — позволяет принцип Гюйгенса- Френеля (1815 г.). Он формулируется в виде двух положений;
- каждый элемент пространства, до которого доходит фронт распространяющейся световой волны, становится источником вторичных световых волн; эти волны сферические; огибающая этих волн дает положение волнового фронта в следующий момент времени;
- вторичные волны когерентны, между собой, поэтому интерферируют при наложении.
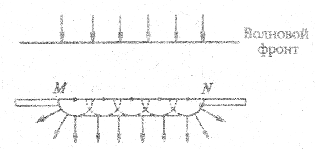 Рассмотрим в качестве примера дифракцию плоских световых воли (дифракцию Фраунгофера) на щели. Ширина щели сравнима с длиной световой волны. Пусть плоская монохроматическая волна с длиной волны λ падает нормально плоскости щели MN (рис. 2.16).
Рассмотрим в качестве примера дифракцию плоских световых воли (дифракцию Фраунгофера) на щели. Ширина щели сравнима с длиной световой волны. Пусть плоская монохроматическая волна с длиной волны λ падает нормально плоскости щели MN (рис. 2.16).
Рис. 2.16.
Каждая точка щели, до которой дошел фронт падающей волны, становится источником вторичных сферических волн, и свет, пройдя узкую щель, распространяется по всем направлениям.
 | |||
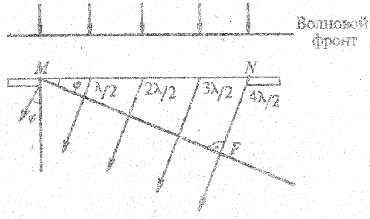 |
Рис. 2.17.
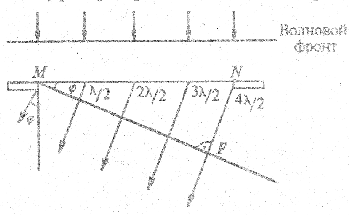
Возьмем произвольное направление хода лучей от щели под углом φ (рис. 2.17). Ясно, что, луч из точки N отстает от луча из точки М на расстояние NF. Это расстояние называется разностью хода лучей. Если ширина щели MN — а, то разность хода равна NF = ∆ = a sinφ. Для анализа удобно разбить щель на несколько зон так, чтобы разность хода, лучей от границ каждой зоны была равна λ/2. При этом волны, соответствующие лучам, будут находиться в противофазе (иметь сдвиг на π). Действительно, фаза волны
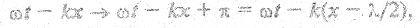
так как

Общее число зон будет равно

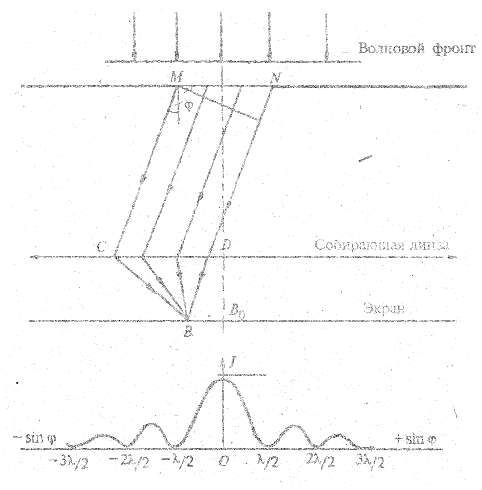 |
Рис. 2.18.
Вторичные лучи фокусируются собирающей линзой и проецируются на экран (рис. 2.18). Согласно принципу Гюйгенса-Френеля вторичные волны интерферируют. Соседние лучи ввиду противофазности соответствующих волн, интерферируя, гасят друг друга. Следовательно, если на щели укладывается четное число зон, то в точке В будет минимум:
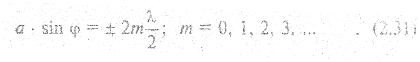
а если не четное – то максимум.
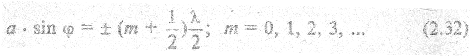

Здесь m - порядок минимума (максимума). В прямом направлении свет дает центральный максимум (точка B0). Распределение интенсивности на экране называется дифракционным спектром.
Если падающий на щель свет монохроматический (например, желтый), то дифракционный спектр будет представлять собой чередующиеся темные и желтые полоски. Если направлять на щель белый свет, являющийся суперпозицией семи монохроматических волн, то для каждой длины волны λi максимумы и минимумы будут наблюдаться под своими углами (φi)max и (φi)min. Дифракционная картина будет выглядеть как чередование “радуг” и темных промежутков, в центре картины будет неокрашенный центральный максимум (максимум нулевого порядка).
Система из большого числа одинаковых и параллельных друг другу щелей называется дифракционной решеткой. Дифракционный спектр от решетки значительно сложнее, чем спектр от одной щели, так как здесь дополнительно интерферируют световые волны от разных щелей. Вместе с тем полосы получаются значительно более яркими, так как через решетку проходит больше света.
Для электромагнитного излучения рентгеновского диапазона естественными дифракционными решетками являются пространственные кристаллические решетки. Это объясняется тем, что расстояния между узлами решеток сравнимы с длинами волн рентгеновского излучения.
Объяснение прямолинейного распространения света. С помощью принципа Гюйгенса-Френеля можно объяснить прямолинейное распространение света. Пусть свет излучается точечным монохроматическим источником S (рис. 2.19).
Согласно принципу Гюйгенса-Френеля заменим действие источника S действием вторичных воображаемых источников, расположенных на, вспомогательной сфере Ф, являющейся волновой поверхностью сферической световой волны. Эта поверхность разбивается на кольцевые зоны так чтобы расстояния от краев зон до точки М отличались на λ/2. Это означает, что волны, приходящие в точку М от каждой зоны отличаются по фазе на π, т. е. любые две «соседние» волны противофазный.
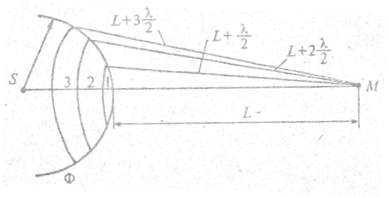
Рис. 2.19.
Амплитуды этих волн при наложении вычитаются, поэтому амплитуда результирующей волны в точке М:
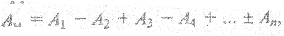 |
где А1,2,…,i,…,n - амплитуда световых волн, возбуждаемых соответствующими зонами. Ввиду очень большого числа зон можно считать, что амплитуда Аi, равна среднему значению амплитуд волн, возбуждаемых примыкающими зонами:
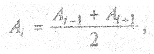
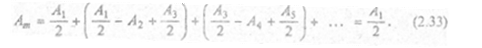 тогда
тогда
Действие всей волны на точке М сводится к действию се малого участка, меньшего, чем центральная зона. Радиус первой зоны имеет порядок десятых долей миллиметра, поэтому распространение света от S к М происходит как бы внутри узкого канала вдоль SM, т. е. прямолинейно.
