Из истории тепловых двигателей
Первой известной нам тепловой машиной была паровая турбина внешнего сгорания, изобретённая во ΙΙ (или в Ι?) веке н. э. в римской империи. Это изобретение не получило своего развития предположительно из-за низкого уровня техники того времени. На прогресс это изобретение никакого влияния не оказало и было забыто. Следующей тепловой машиной, изобретённой человеком, была пороховая ракета и пороховое орудие. Дата его изобретения неизвестна, первое известное упоминание относится к 13 веку. Это произошло в Китае. Это было простое устройство, которое с точки зрения инженера и механика не является тепловым двигателем, так как не имеет вала отбора мощности, но с точки зрения физики является тепловой машиной. Поэтому этот прибор имеет ограниченное применение: для связи, в военном деле, как транспорт (в последнем случае есть проблемы, но в принципе это возможно). В 17 веке изобретательская мысль попыталась на базе порохового орудия создать тепловой двигатель.
В поршневых тепловых двигателях горячий газ расширяется в цилиндре, перемещая поршень, и тем самым совершает механическую работу. Для превращения прямолинейного возвратно-поступательного движения поршня во вращательное движение вала обычно используется кривошипно-шатунный механизм. В двигателях внешнего сгорания (например, в паровых машинах) рабочее тело нагревают за счет сжигания топлива вне двигателя и подают в цилиндр газ (пар) под высокими температурой и давлением. Газ, расширяясь и перемещая поршень, охлаждается, а давление его падает до близкого к атмосферному. Этот отработанный газ удаляется из цилиндра, а затем в него подается новая порция газа - либо после возврата поршня в исходное положение (в двигателях одинарного действия - с односторонним впуском), либо с обратной стороны поршня (в двигателях двойного действия). В последнем случае поршень возвращается в исходное положение под действием расширяющейся новой порции газа, а в двигателях одинарного действия поршень возвращается в исходное положение маховиком, установленным на валу кривошипа. В двигателях двойного действия на каждый оборот вала приходится два рабочих хода, а в двигателях одинарного действия - только один; поэтому первые двигатели в два раза мощнее при одинаковых габаритах и скоростях. В двигателях внутреннего сгорания горячий газ, который перемещает поршень, получают за счет сжигания смеси топлива и воздуха непосредственно в цилиндре. Для подвода свежих порций рабочего тела и выпуска отработанного газа в двигателях применяется система клапанов. Подвод и выпуск газа производятся при строго определенных положениях поршня, что обеспечивается специальным механизмом, который управляет работой впускных и выпускных клапанов.
Холодильная машина
Холодильная машина – периодически действующая установка, в которой за счёт работы внешних сил теплота переносится к телу с более высокой температурой 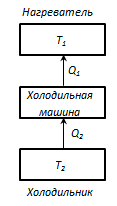 (рис. 130).
(рис. 130).
Рис. 130.
В основе действия холодильной машины лежит обратный цикл Карно: системой за цикл от термостата с более низкой температурой Т2 отнимается количество теплоты 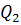 и отдаётся термостату с более высокой температурой Т1 количество теплоты
и отдаётся термостату с более высокой температурой Т1 количество теплоты 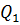 .
.
Для кругового процесса 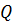 = А, но согласно условию
= А, но согласно условию 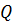 =
= 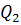 -
- 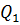 < 0, поэтому А < 0 и
< 0, поэтому А < 0 и 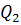 -
- 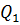 = - А или
= - А или 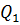 =
= 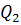 + А, т.е. количество теплоты
+ А, т.е. количество теплоты 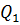 , отданное системой источнику теплоты при более высокой температуре Т1, больше количества теплоты
, отданное системой источнику теплоты при более высокой температуре Т1, больше количества теплоты 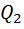 , полученного от источника теплоты при более низкой температуре Т2, на величину работы, совершённой над системой. Следовательно, без совершения работы нельзя отбирать теплоту от менее нагретого тела и отдавать её более нагретому.
, полученного от источника теплоты при более низкой температуре Т2, на величину работы, совершённой над системой. Следовательно, без совершения работы нельзя отбирать теплоту от менее нагретого тела и отдавать её более нагретому.
Эффективность холодильной машины характеризуется холодильным коэффициентом:
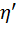 =
= 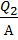 =
= 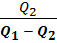 .
.
Здесь полезным эффектом выступает теплота 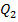 , затраченным – абсолютное значение совершенной работы.
, затраченным – абсолютное значение совершенной работы.
Для обратимых циклов существует взаимосвязь: 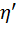 =
=  - 1.
- 1.
Цикл Карно[40]
Цикл Карно назван в честь французского учёного и инженера Сади Карно, который впервые его описал в своём сочинении «О движущей силе огня и о машинах, способных развивать эту силу» в 1824 году.
Циклом Карно называется обратимый круговой процесс, состоящий из двух изотерм и двух адиабат.
Среди всех циклов ему принадлежит особое место, т.к. он является наиболее экономичным и лежит в основе действия идеальной тепловой машины. Рассмотрим прямой цикл Карно (рис. 131).
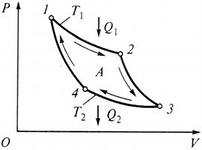
Рис. 131.
| Последовательные термодинамические процессы | |
Изотермическое расширение 1 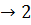 T= const; V2 > V1 T= const; V2 > V1 | A12 = 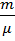 RT1ln RT1ln 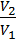 = = 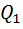 |
Адиабатное расширение 2 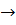 3 3 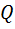 = 0; T2 < T1 = 0; T2 < T1 | A23 = 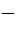 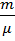 CV (T2 CV (T2 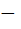 T1) T1) |
Изотермическое сжатие 3 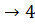 T=const; V2 < V1 T=const; V2 < V1 | A34 =  RT2 ln RT2 ln 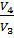 = = 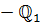 |
Адиабатное сжатие 4 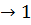 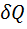 = 0; T1 > T2 = 0; T1 > T2 | A41 = 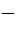 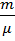 CV (T1 CV (T1 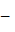 T2) = T2) = 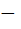 A23 A23 |
Работа за цикл:
A = A12 + A23 + A34 + A41 = 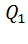 + A23
+ A23 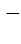
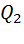
 A23 =
A23 = 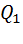

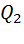 (1)
(1)
и определяется площадью, ограниченной рассматриваемыми изотермами и адиабатами (рис. 100).
Адиабатические процессы в цикле Карно носят вспомогательный характер: они помогают перейти с одной изотермы на другую. В энергетическом балансе эти процессы не участвуют, т.к. работа адиабатного расширения и адиабатного сжатия компенсируют друг друга.
В процессе Карно термодинамическая система выполняет механическую работу и обменивается теплотой с двумя тепловыми резервуарами, имеющими постоянные, но различающиеся температуры. Резервуар с более высокой температурой называется нагревателем, а с более низкой температурой — холодильником.
Пусть рабочим телом машины, работающей по циклу Карно, является моль ( 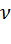 = 1 моль) идеального газа, тогда теплота
= 1 моль) идеального газа, тогда теплота 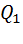 , взятая от нагревателя, определяется работой изотермического расширения газа от объёма V1 до объёма V2:
, взятая от нагревателя, определяется работой изотермического расширения газа от объёма V1 до объёма V2: 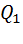 = RT1ln
= RT1ln 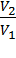 . (2)
. (2)
Теплота, переданная рабочим телом холодильнику, определяется работой изотермического сжатия газа от объёма V3 до объёма V4:
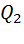 = RT2 ln
= RT2 ln 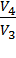 =
=  RT2 ln
RT2 ln 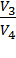 . (3)
. (3)
Тогда: A = 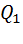

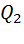 = RT1ln
= RT1ln 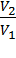
 RT2 ln
RT2 ln 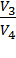 .
.
Общее выражение КПД для циклического процесса:
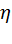 =
= 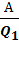 =
= 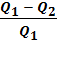 =1
=1 
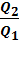 (4)
(4)
для цикла Карно с идеальным газом примет вид:
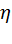 =
= 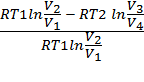 . (5)
. (5)
Из уравнения Пуассона T 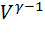 = const, применённого к адиабатическим участкам цикла, легко получить :
= const, применённого к адиабатическим участкам цикла, легко получить : 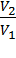 =
= 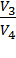 . Это позволяет сократить дробь (5) на величину Rln
. Это позволяет сократить дробь (5) на величину Rln 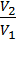 = R ln
= R ln 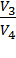 и получить для КПД идеального цикла Карно:
и получить для КПД идеального цикла Карно: 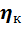 =
= 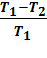 < 1
< 1  (6)
(6)
Так как абсолютный нуль температур недостижим (T2 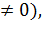 то КПД идеальной тепловой машины всегда меньше единицы.
то КПД идеальной тепловой машины всегда меньше единицы.
Формула (6) выражает теорему Карно:
КПД идеальной тепловой машины, работающей по циклу Карно, максимален и не зависит от природы рабочего вещества и конструкции тепловой машины, он определяется только по температурам нагревателя ( 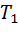 ) и холодильника (T2).
) и холодильника (T2).
Поскольку обратимые процессы могут осуществляться лишь с бесконечно малой скоростью, мощность тепловой машины в цикле Карно равна нулю. Мощность реальных тепловых машин не может быть равна нулю, поэтому реальные процессы могут приближаться к идеальному обратимому процессу Карно только с большей или меньшей степенью точности. В цикле Карно тепловая машина преобразует теплоту в работу с максимально возможным коэффициентом полезного действия из всех тепловых машин, у которых максимальная и минимальная температуры в рабочем цикле совпадают соответственно с температурами нагревателя и холодильника в цикле Карно.
КПД необратимой тепловой машины всегда меньше, чем обратимой, работающей в аналогичных условиях (т.е. с теми же нагревателем и холодильником). Так КПД современных паровых машин не превышает 25%, двигателей внутреннего сгорания – 40%. Между тем теоретический предел лежит выше. Снижение КПД реальных тепловых машин по сравнению с теоретическим вызвано необратимыми процессами, которые происходят в самой тепловой машине (теплопроводностью и т.п.).
Пути повышения КПД тепловых машин: устранение (по мере возможности) и ослабление необратимых процессов. Если необратимый процесс всё же произошёл, то нет ни какой возможности устранить его последствия, ведущие к ухудшению работы двигателя.
В тепловых двигателях стремятся обеспечить наилучшую отдачу тепла рабочему телу и наименьшую потерю тепла рабочим веществом. Так, чтобы сократить число необратимых процессов теплообмена в двигателях внутреннего сгорания, «внесли» топку внутрь рабочего цилиндра. Осуществляют и другие мероприятия.
Второе начало термодинамики
Исторически второе начало термодинамики возникло из анализа работы тепловых машин (С. Карно, 1824). Существует несколько его эквивалентных формулировок. Само название «второе начало термодинамики» и исторически первая его формулировка (1850) принадлежат Р. Клаузиусу.
Первое начало термодинамики, выражая закон сохранения и превращения энергии, не позволяет установить направление протекания термодинамических процессов. Кроме того, можно представить множество процессов, не противоречащих первому началу, в которых энергия сохраняется, а в природе они не осуществляются.
Опыт показывает, что разные виды энергии неравноценны в отношении способности превращаться в другие виды энергии. Механическую энергию можно целиком превратить во внутреннюю энергию любого тела. Для обратных превращений внутренней энергии в другие виды существуют определённые ограничения: запас внутренней энергии ни при каких условиях не может превратиться целиком в другие виды энергии. С отмеченными особенностями энергетических превращений связано направление протекания процессов в природе.
Второе начало термодинамики - принцип, устанавливающий необратимость макроскопических процессов, протекающих с конечной скоростью.
В отличие от чисто механических (без трения) или электродинамических (без выделения джоулевой теплоты) обратимых процессов, процессы, связанные с теплообменом при конечной разности температур (т. е. текущие с конечной скоростью), с трением, диффузией газов, расширением газов в пустоту, выделением джоулевой теплоты и т.д., необратимы, т. е. могут самопроизвольно протекать только в одном направлении.
Второе начало термодинамики отражает направленность естественных процессов и налагает ограничения на возможные направления энергетических превращений в макроскопических системах, указывая, какие процессы в природе возможны, а какие – нет.
Второе начало термодинамики является постулатом, не доказываемым в рамках термодинамики. Оно было создано на основе обобщения опытных фактов и получило многочисленные экспериментальные подтверждения.
Формулировки второго закона термодинамики
1). формулировка Карно: наибольший КПД тепловой машины не зависит от рода рабочего тела и вполне определяется предельными температурами, между которыми машина работает.
2). формулировка Клаузиуса: невозможен процесс единственным результатом которого является передача энергии в форме теплоты от тела менее нагретого, к телу более нагретому.
Второе начало термодинамики не запрещает переход теплоты от менее нагретого тела к более нагретому. Такой переход осуществляется в холодильной машине, но при этом внешние силы осуществляют работу над системой, т.е. этот переход не является единственным результатом процесса.
3). формулировка Кельвина: невозможен круговой процесс, единственным результатом которого является превращение теплоты, полученной от нагревателя, в эквивалентную ей работу.
На первый взгляд может показаться, что такой формулировке противоречит изотермического расширения идеального газа. Действительно, всё полученное идеальным газом от какого-то тела тепло превращается полностью в работу. Однако получение тепла и превращение его в работу не единственный конечный результат процесса; кроме того, в результате процесса происходит изменение объёма газа.
P.S.: необходимо обратить внимание на слова «единственным результатом»; запреты второго начала снимаются, если процессы, о которых идёт речь, не являются единственными.
4). формулировка Оствальда[41]: осуществление вечного двигателя второго рода невозможно.
Вечным двигателем второго рода называется периодически действующее устройство, которое совершает работу за счёт охлаждения одного источника теплоты.
Примером такого двигателя мог бы служить судовой двигатель, получающий тепло из моря и использующий его для движения судна. Такой двигатель был бы практически вечным, т.к. запас энергии в окружающей среде практически безграничен.
С точки зрения статистической физики второе начало термодинамики имеет статистический характер: оно справедливо для наиболее вероятного поведения системы. Существование флуктуаций препятствует точному его выполнению, однако вероятность сколь-нибудь значительного нарушения крайне мала.
Энтропия
Понятие «энтропия» введено в науку Р.Клаузиусом в 1862 г. и образовано из двух слов: «эн» - энергия, «тропэ» - превращаю.
Согласно нулевому началу термодинамики изолированная термодинамическая система с течением времени самопроизвольно переходит в состояние термодинамического равновесия и остаётся в нём сколь угодно долго, если внешние условия сохраняются неизменными.
В равновесном состоянии все виды энергии системы переходят в тепловую энергию хаотического движения атомов и молекул, составляющих систему. Никакие макроскопические процессы в такой системе невозможны.
Количественной мерой перехода изолированной системы в равновесное состояние служит энтропия. По мере перехода системы в равновесное состояние её энтропия возрастает и достигает максимума при достижении равновесного состояния.
Энтропия является функцией состояния термодинамической системы, обозначается: [S] = 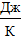 .
.
Теоретическое обоснование: приведённая теплота, энтропия
Из выражения для КПД цикла Карно: 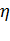 =
= 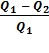 = =
= = 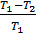 следует, что
следует, что 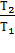 =
= 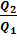 или
или 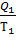

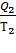 = 0, где
= 0, где 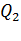 - количество теплоты, отдаваемое рабочим телом холодильнику, принимаем:
- количество теплоты, отдаваемое рабочим телом холодильнику, принимаем: 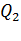 < 0.
< 0.
Тогда последнее соотношение можно записать в виде:
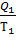 +
+ 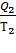 = 0 (1)
= 0 (1)
Отношение теплоты, полученной телом в изотермическом процессе, к температуре теплоотдающего тела называется приведённым количеством теплоты: 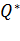 =
= 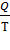 . (2)
. (2)
С учётом формулы (2) формулу (1) представим в виде:
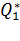 +
+ 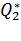 = 0, (3)
= 0, (3)
т.е. для цикла Карно алгебраическая сумма приведённых количеств теплоты равна нулю.
Приведённое количество теплоты, сообщаемое телу на бесконечно малом участке процесса: 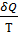 .
.
Приведённое количество теплоты для произвольного участка:
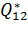 =
= 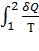 .
.
Строгий теоретический анализ показывает, что для любого обратимого кругового процесса сумма приведённых количеств теплоты равна нулю:
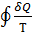 = 0. (4)
= 0. (4)
Из равенства нулю интеграла (4) следует, что подинтегральная функция 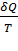 есть полный дифференциал[42] некоторой функции, которая определяется только состоянием системы и не зависит от пути, каким система пришла в это состояние:
есть полный дифференциал[42] некоторой функции, которая определяется только состоянием системы и не зависит от пути, каким система пришла в это состояние:
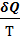 = dS. (5)
= dS. (5)
Однозначная функция состояния, полным дифференциалом которой является 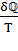 , называется энтропией S, (
, называется энтропией S, ( 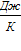 ).
).
Формула (5) справедлива лишь для обратимых процессов, в случае неравновесных необратимых процессов такое представление dS несправедливо.
Свойства энтропии
1). Энтропия определяется с точностью до произвольной постоянной. Физический смысл имеет не сама энтропия, а разность энтропий двух состояний:
∆S = S2  S1 =
S1 = 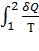 . (6)
. (6)
Пример: если система (идеальный газ) совершает равновесный переход из состояния 1 в состояние 2, то изменение энтропии равно:
∆S12 = S2  S1 =
S1 = 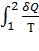 =
= 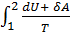 ,
,
где dU = 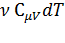 ;
; 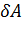 = P dV =
= P dV = 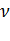 RT
RT 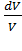 .
.
Тогда: ∆S12 = = 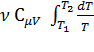 +
+ 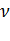 R
R 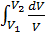 =
= 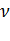 (
( 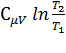 + R ln
+ R ln 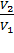 ),
),
т.е. изменение энтропии ∆S12 идеального газа при переходе его из состояния 1 в состояние 2 не зависит от вида процесса перехода.
В общем случае в формуле (6) приращение энтропии ∆S не зависит от пути интегрирования.
2). Абсолютное значение энтропии можно установить с помощью третьего начала термодинамики (теоремы Нернста[43]):
Энтропия любого тела стремиться к нулю при стремлении к абсолютному нулю его температуры: 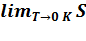 = 0.
= 0.
Таким образом, за начальную точку отсчёта энтропии принимают S0 = 0 при T = 0 K.
3). Энтропия величина аддитивная, т.е. энтропия системы из нескольких тел является суммой энтропий каждого тела: S = 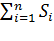 .
.
4). Как и внутренняя энергия, энтропия есть функция параметров термодинамической системы P, V, T.
5), Процесс, протекающий при постоянной энтропии (S=const) называется изоэнтропийным.
В равновесных процессах без передачи тепла ( 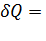 0) энтропия не меняется.
0) энтропия не меняется.
В частности, изоэнтропийным является обратимый адиабатный процесс: для него 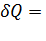 0; ∆S = 0, т.е. S = const.
0; ∆S = 0, т.е. S = const.
6). При постоянном объёме (V = const) энтропия является монотонно возрастающей функцией внутренней энергии тела.
Действительно, из первого закона термодинамики следует, что при dV = 0 имеем: 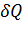 = dU, тогда dS =
= dU, тогда dS = 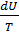 . Но температура T > 0 всегда. Поэтому приращения dS и dU имеют один и тот же знак, что и требовалось доказать.
. Но температура T > 0 всегда. Поэтому приращения dS и dU имеют один и тот же знак, что и требовалось доказать.
Примеры изменения энтропии в различных процессах
1). При изобарном расширении идеального газа
∆S = 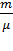 CP ln
CP ln 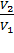 .
.
2). При изохорном расширении идеального газа
∆S = 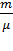 CV ln
CV ln 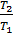 .
.
3). При изотермическом расширении идеального газа
∆S = 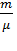 R ln
R ln 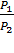 =
= 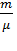 R ln
R ln 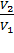 .
.
4). При фазовых переходах
Пример: найти изменение энтропии при превращении массы mл льда при температуре Т1 в пар (Тп = 373 К).
Решение
Первый закон термодинамики: 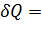 dU +
dU + 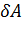 =
= 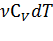 + P dV.
+ P dV.
Из уравнения Менделеева – Клапейрона следует: P = 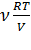 =>
=> 
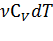 +
+ 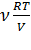 dV.
dV.
При переходе из одного агрегатного состояния в другое, общее изменение энтропии складывается из изменений в отдельных процессах:
а). Нагревание льда от температуры Т1 до температуры плавления Т0 = 273 К:
∆S1 = 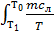 dT = mcл ln
dT = mcл ln 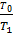 ,
,
где cл – удельная теплоёмкость льда.
б). Плавление льда: ∆S2 = 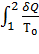 =
= 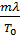 , где
, где  - удельная теплота плавления льда.
- удельная теплота плавления льда.
в). Нагревание воды от температуры Т0 до температуры кипения Тк = 273 К:
∆S3 = 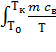 dT = mcв ln
dT = mcв ln 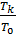 , где св – удельная теплоёмкость воды.
, где св – удельная теплоёмкость воды.
г). Испарение воды: ∆S4 = 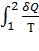 =
= 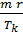 , где r – удельная теплота парообразования воды.
, где r – удельная теплота парообразования воды.
Тогда общее изменение энтропии:
∆S = ∆S1 + ∆S2 + ∆S3 + ∆S4 = mcл ln 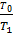 +
+ 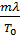 + mcв ln
+ mcв ln 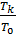 +
+ 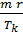 .
.
Принцип возрастания энтропии
Энтропия замкнутой системы при любых, происходящих в ней процессах не убывает:
dS 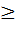 0,
0,
или для конечного процесса: ∆S 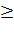 0 => S2
0 => S2 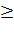 S1.
S1.
Знак равенства относится к обратимому процессу, знак неравенства – к необратимому. Последние две формулы – математическое выражение второго закона термодинамики. Таким образом, введение понятия «энтропия» позволило строго математически сформулировать второе начало термодинамики.
Необратимые процессы приводят к установлению равновесного состояния. В этом состоянии энтропия изолированной системы достигает максимума. Никакие макроскопические процессы в такой системе невозможны.
Величина изменения энтропии является качественной характеристикой степени необратимости процесса.
Принцип возрастания энтропии относится к изолированным системам. Если система неизолированная, то её энтропия может и убывать.
Вывод: т.к. все реальные процессы необратимые, то все процессы в замкнутой системе ведут к увеличению её энтропии.
Теоретическое обоснование принципа
Рассмотрим замкнутую систему, состоящую из нагревателя, холодильника, рабочего тела и «потребителя» совершаемой работы (тело, обменивающееся с рабочим телом энергией только в форме работы), совершающую цикл Карно. Это обратимый процесс, изменение энтропии которого равно:
∆S = ∆Sр + ∆Sн + ∆Sх + ∆Sп,
где ∆Sр – изменение энтропии рабочего тела; ∆Sн – изменение энтропии нагревателя; ∆Sх – изменение энтропии холодильника; ∆Sп – изменение энтропии «потребителя» работы.
Так как рабочее тело при совершении цикла Карно возвращается в исходное положение, то ∆Sр = 0. Так как «потребитель» работы получает энергию в форме работы, то ∆Sп = 0.
Изменение энтропии нагревателя и холодильника в изотермических процессах:
∆Sн = 
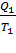 ; ∆Sх =
; ∆Sх = 
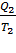 ,
,
где 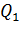 и
и 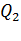 - количество теплоты, полученной рабочим телом за один цикл соответственно от нагревателя (
- количество теплоты, полученной рабочим телом за один цикл соответственно от нагревателя ( 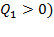 и холодильника (
и холодильника ( 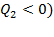 .
.
С учётом выше изложенного изменение энтропии системы равно:
∆S =  (
( 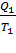 +
+ 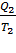 ).
).
Так как цикл Карно обратимый, то КПД цикла равен: 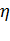 =
= 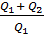 =
= 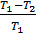
или 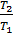 =
= 
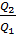 .
.
В результате получаем, что энтропия замкнутой системы, совершающей обратимый цикл, не изменяется: ∆Sобр. = 0, т.е. S = const.
Все реальные процессы необратимы. Рассмотрим необратимый цикл. КПД необратимого цикла всегда меньше КПД цикла Карно:
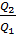 < (
< ( 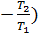 и
и 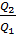 +
+ 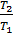 < 0 |
< 0 | 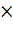
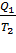 =>
=> 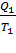 +
+ 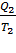 < 0,
< 0,
т.е. энтропия замкнутой системы, совершающей необратимый цикл, возрастает:
∆Sнеобр. > 0.
Эти выводы можно обобщить для произвольных процессов в замкнутой системе в виде принципа возрастания энтропии.
Основное соотношение термодинамики. Свободная энергия
Первый закон термодинамики: 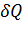 = dU +
= dU + 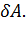 (1)
(1)
Изменение энтропии обратимого процесса: dS = 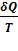 .(2)
.(2)
Второй закон термодинамики: dS 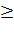 0. (3)
0. (3)
Из формул (2) и (3) следует: 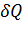
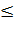 T dS, (4)
T dS, (4)
где Т – температура тела, сообщающего системе энергию 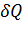 в процессебесконечно малого изменения состояния системы.
в процессебесконечно малого изменения состояния системы.
Объединив первый и второй законы термодинамики, получим основное соотношение термодинамики: T dS 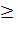 dU +
dU + 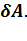 (5)
(5)
Основное соотношение термодинамики для обратимого процесса:
T dS = dU + 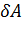 (6)
(6)
или 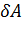 =
=  (dU
(dU  T dS) =
T dS) =  d (U
d (U  TS)
TS)  S dT =
S dT =  dF
dF  S dT,
S dT,
где F = U  TS – свободная энергия (энергия Гельмгольца[44]). (7)
TS – свободная энергия (энергия Гельмгольца[44]). (7)
Свободная энергия F является разностью двух функций состояний и поэтому то же является функцией состояния термодинамической системы.
Рассмотрим обратимый изотермический процесс, когда dT = 0 и 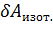 =
=  dF.
dF.
При переходе системы из состояния 1 в состояние 2 в обратимом изотермическом процессе: Аизот. = F1  F2.
F2.
Таким образом, убыль свободной энергии является мерой работы, которую система совершает в обратимом изотермическом процессе.
Из формулы (7) следует: U = F + TS, где TS – связанная энергия. (8)
