Изучение режимов движения жидкости
Цель работы – визуально наблюдать режимы движения жидкости, установить опытным путем критическое значение числа Рейнольдса, соответствующее переходу ламинарного режима в турбулентный.
Теоретическая часть. Существует два режима течения: ламинарный и турбулентный. Обычно при малых скоростях струйки жидкости движутся параллельно, скользя относительно друг друга. При непрерывном возрастании скорости потока будут нарастать потери напора из-за трения жидкости (пропорционально скорости). Такой режим называется ламинарным. Когда значение числа Рейнольдса (Re), определяемого средней скоростью потока J, диаметром трубы d, плотностью жидкости r и динамической вязкостью жидкости m достигнет определенного критического значения (Reкр = 2300), режим движения резко, скачкообразно начинает меняться. Проявляет действие всеобщий закон о переходе количества в качество. При больших скоростях наблюдается поперечное перемещение струек жидкости за счет образования вихрей. Потери напора на трение будут нарастать и стремиться к квадратичной зависимости от скорости.
Если Re < 2300, то должен иметь место ламинарный режим; если Re > 2300, то режим турбулентный.
Необходимо отметить, что приведенное критическое значение число Рейнольдса является в известной степени условной величиной, так как трудно обнаружить резкий переход от ламинарного режима к турбулентному. В действительности наблюдается так называемая «переходная» область исчезновения ламинарного режима, установления турбулентного состояния потока. Числовые значения критерия Рейнольдса для неразвитого турбулентного режима находятся в пределах 2300 ¸ 10000. При Re > 10000 режим потока становится развитым турбулентным.
При уменьшении скорости жидкости возможен обратный переход к ламинарному режиму движения.
При движении реальных жидкостей возникают силы сопротивления, вследствие чего как при ламинарном, так и при турбулентном режиме часть напора теряется на преодоление гидравлических сопротивлений. Эти потери различны, так как условия движения жидкости при разных режимах различны, поэтому при проведении гидравлических расчетов систем и решении задач, связанных с движением жидкости, необходимо вначале установить режим движения жидкости.
В большинстве технологических аппаратов наблюдается турбулентный режим движения, обеспечивающий более интенсивное протекание тепломассообменных процессов.
Описание установки
Установка для определения числа Рейнольдса (рис.2.3) состоит из напорного бака 1, питательного трубопровода 2 с регулирующим вентилем 3, успокоителя 4, мерного бака 5, стеклянной трубы 6 диаметром 0,03 м, предназначенной для наблюдения за режимами движения, и бачка с раствором красителя 7. Во избежание переполнения бака в нем предусмотрен водослив. Подача красителя регулируется краном 8.

Методика проведения работы
Наполнить водой напорный бак 1. Уровень воды в баке при проведении опытов должен поддерживаться постоянным. Это достигается с помощью водослива.
Все опыты проводить при установившихся потоках.
Приоткрыть вентиль 3 на питательном трубопроводе и для подачи красителя открыть кран 8. Подкрашенная струйка при ламинарном режиме должна быть прямой. Зарисовать наблюдаемую картину движения жидкости в трубе.
Открывая вентиль 3 и плавно увеличивая расход воды, добиться начала разрушения ламинарного режима. При некотором открытии вентиля окрашенная струйка начинает искривляться и становиться волнообразной.
Закрыть кран на сливной трубе 9 и определить расход жидкости и помощью мерного бака и секундомера. Измерить температуру воды и найти соответствующее значение кинематического коэффициента вязкости (приложение А).
По полученному значению расхода и критической скорости определить критическое значение числа Рейнольдса, соответствующее переходу ламинарного режима в турбулентный (определение Reкр повторить не менее 3-х раз).
Открыть полностью вентиль 3. Наблюдать турбулентный режим течения и зарисовать картину движения ее подкрашенной части.
Обработка результатов эксперимента
Определить расход, м3/с
 , (2.5)
, (2.5)
где W – объем жидкости в мерном баке, м3; t - время наполнения, с.
Определить среднюю скорость движения, м/с
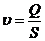 , (2.6)
, (2.6)
где S – площадь сечения трубы, м2.
Определить число Рейнольдса
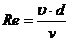 . (2.7)
. (2.7)
Результаты опытов и расчетов внести в табл.2.2.
Таблица 2.2
| Наименование параметра | Опыт 1 | Опыт 2 | Опыт 3 |
| Объем жидкости в мерном баке W, м3 | |||
| Время наполнения t, с | |||
| Расход воды в трубе Q, м3/с | |||
Средняя скорость движения 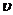 , м/с , м/с | |||
| Число Рейнольдса Re | |||
| Режим движения |
Контрольные вопросы
1. Ламинарный режим движения, его особенности.
2. Турбулентный режим движения, его особенности.
3. Число Рейнольдса для цилиндрических труб и для потоков с некруглым сечением.
4. Значение режима движения для расчета трубопроводов.
5. Причины разрушения ламинарного режима.
Список основных источников: [1, с.62-65; 2, с.65-67; 3, с.38-41].
Лабораторная работа № 3
