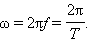При любых физических взаимодействиях энергия не возникает и не исчезает. Она лишь превращается из одной формы в другую.
Этот экспериментально установленный факт выражает фундаментальный закон природы – закон сохранения и превращения энергии.
Одним из следствий закона сохранения и превращения энергии является утверждение о невозможности создания «вечного двигателя» (perpetuum mobile) – машины, которая могла бы неопределенно долго совершать работу, не расходуя при этом энергии (рис. 1.1.17).
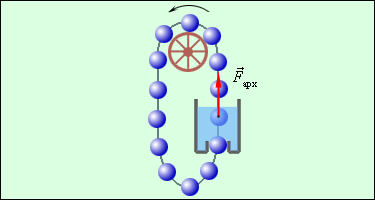 |
| Рисунок 1.1.17. Один из проектов «вечного двигателя». Почему эта машина не будет работать? |
История хранит немалое число проектов «вечного двигателя». В некоторых из них ошибки «изобретателя» очевидны, в других эти ошибки замаскированы сложной конструкцией прибора, и бывает очень непросто понять, почему эта машина не будет работать. Бесплодные попытки создания «вечного двигателя» продолжаются и в наше время. Все эти попытки обречены на неудачу, так как закон сохранения и превращения энергии «запрещает» получение работы без затраты энергии.
МЕТОДИКА И ПОРЯДОК ИЗМЕРЕНИЙ:
Внимательно рассмотрите окно опыта. Найдите все регуляторы и другие основные элементы. Зарисуйте в свой конспект схему опыта.
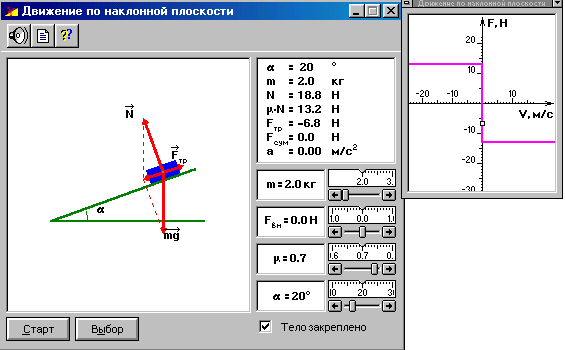
После нажатия мышью кнопки «Выбор» установите с помощью движков регуляторов значения массы тела m, угла наклона плоскости a, внешней силы Fвн, коэффициента трения m и ускорения а, указанных в табл.1 для вашей бригады.
Потренируйтесь в синхронном включении секундомера и снятия метки «тело закреплено» одиночным щелчком курсора мыши на кнопке в правом нижнем углу окна опыта
Одновременно включите секундомер и снимите метку «тело закреплено». Выключите секундомер в момент остановки тела в конце наклонной плоскости.
Проделайте этот опыт 10 раз и результаты измерения времени соскальзывания тела с наклонной плоскости запишите в табл. 2.
ТАБЛИЦА 1. Исходные параметры опыта
| № бриг. | ||||||||
| m, кг | 2,0 | 2,2 | 2,4 | 2,6 | 2,8 | 3,0 | 2,9 | 2,7 |
| m | 0,10 | 0,14 | 0,18 | 0,22 | 0,26 | 0,30 | 0,34 | 0,38 |
| a,град | ||||||||
| Fвн, Н | -4 | -3 | -2 | -1 | ||||
| а,м/с2 |
ТАБЛИЦА 2. Результаты измерений и расчётов
| № изм. | Сред. знач. | d | ||||||||||
| t, с | ||||||||||||
| v, м/с | ||||||||||||
| S, м | ||||||||||||
| Wк, Дж | ||||||||||||
| Wп , Дж | ||||||||||||
| Aтр, Дж | ||||||||||||
| Aвн , Дж | ||||||||||||
| Wполн, Дж |
ОБРАБОТКА РЕЗУЛЬТАТОВ И ОФОРМЛЕНИЕ ОТЧЁТА:
Вычислите по формулам:
а) 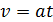 - скорость тела в конце наклонной плоскости;
- скорость тела в конце наклонной плоскости;
б) 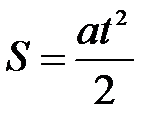 - длину наклонной плоскости;
- длину наклонной плоскости;
в) 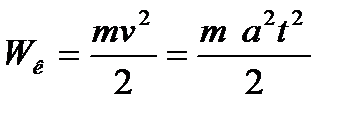 - кинетическую энергию тела, в конце наклонной плоскости;
- кинетическую энергию тела, в конце наклонной плоскости;
г) 
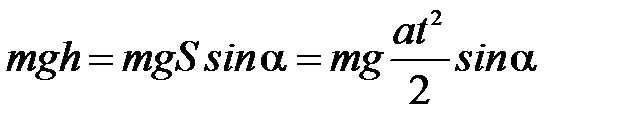 - потенциальную энергию тела в верхней точке наклонной плоскости;
- потенциальную энергию тела в верхней точке наклонной плоскости;
д) 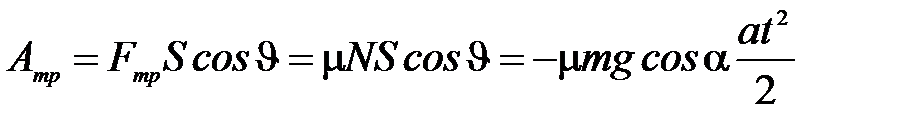 - работу силы трения на участке спуска;
- работу силы трения на участке спуска;
е) 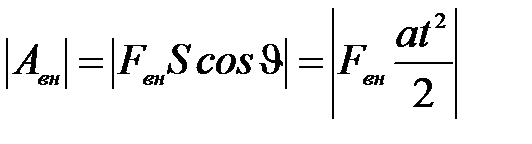 - работу внешней силы на участке спуска (определите знак работы исходя из условий эксперимента)
- работу внешней силы на участке спуска (определите знак работы исходя из условий эксперимента)
и запишите эти значения в соответствующие строки табл. 2.
Вычислите средние значения этих параметров и запишите их в столбец «средние значения» табл.2.
По формуле Емех1 = Емех2 проверьте выполнение закона сохранения механической энергии при движении тела по наклонной плоскости, рассчитайте погрешности и сделайте выводы по результатам проведённых опытов.
Вопросы и задания для самоконтроля
1. В чём заключается закон сохранения механической энергии?
2. Для каких систем выполняется закон сохранения механической энергии?
3. В чём состоит различие между понятиями энергии и работы?
4. Чем обусловлено изменение потенциальной энергии?
5. Чем обусловлено изменение кинетической энергии?
6. Необходимо ли выполнение условия замкнутости механической системы тел для выполнения закона сохранения механической энергии?
7. Какие силы называются консервативными?
8. Какие силы называются диссипативными?
9. Тело медленно втаскивают в гору. Зависят ли от формы профиля горы: а) работа силы тяжести; б) работа силы трения? Начальная и конечная точки перемещения тела фиксированы.
10. Тело соскальзывает с вершины наклонной плоскости без начальной скорости. Зависит ли работа силы трения на всём пути движения тела до остановки на горизонтальном участке: а) от угла наклона плоскости; б) от коэффициента трения?
11. По наклонной плоскости с одной и той же высоты соскальзывают два тела: одно массой m, другое массой 2m. Какое из тел пройдёт до остановки по горизонтальному участку путь больший и во сколько раз? Коэффициенты трения для обоих тел одинаковы.
12. Санки массой m скатились с горы высотой Н и остановились на горизонтальном участке. Какую работу необходимо совершить для того, чтобы поднять их на гору по линии скатывания.
13. С одинаковой начальной скоростью тело проходит: а) впадину; б) горку, имеющие одинаковые дуги траекторий и одинаковые коэффициенты трения. Сравните скорости тела в конце пути в обоих случаях.
ЛАБОРАТОРНАЯ РАБОТА № 1_2
МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
Ознакомьтесь с конспектом лекций и учебником. Запустите программу. Выберите «Механика», «Механические колебания и волны» и «Свободные колебания» (сначала математический маятник, потом груз на пружине). Нажмите вверху внутреннего окна кнопку с изображением страницы. Прочитайте краткие теоретические сведения. Необходимое запишите в свой конспект. (Если вы забыли, как работать с системой компьютерного моделирования, прочитайте ВВЕДЕНИЕ еще раз.
ЦЕЛЬ РАБОТЫ:
* Выбор физических моделей для анализа движения тел.
* Исследование движения тела под действием квазиупругой силы.
* Экспериментальное определение зависимости частоты колебаний от параметров системы.
*
КРАТКАЯ ТЕОРИЯ:
Механические колебания
Гармонические колебания
В технике и окружающем нас мире часто приходится сталкиваться с периодическими (или почти периодическими) процессами, которые повторяются через одинаковые промежутки времени. Такие процессы называют колебательными. Колебательные явления различной физической природы подчиняются общим закономерностям. Например, колебания тока в электрической цепи и колебания математического маятника могут описываться одинаковыми уравнениями. Общность колебательных закономерностей позволяет рассматривать колебательные процессы различной природы с единой точки зрения.
Наряду с поступательными и вращательными движениями тел в механике значительный интерес представляют и колебательные движения. Механическими колебаниями называют движения тел, повторяющиеся точно (или приблизительно) через одинаковые промежутки времени. Закон движения тела, совершающего колебания, задается с помощью некоторой периодической функции времени x = F(t). Графическое изображение этой функции дает наглядное представление о протекании колебательного процесса во времени.
Примерами простых колебательных систем могут служить груз на пружине или математический маятник (рис. 1.2.1).
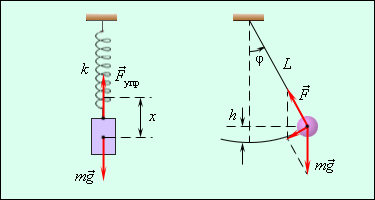 |
| Рисунок 1.2.1. Механические колебательные системы. |
Механические колебания, как и колебательные процессы любой другой физической природы, могут быть свободными и вынужденными. Свободные колебаниясовершаются под действием внутренних сил системы, после того, как система была выведена из состояния равновесия. Колебания груза на пружине или колебания маятника являются свободными колебаниями. Колебания, происходящие под действием внешних периодически изменяющихся сил, называются вынужденными (см. §2.5).
Простейшим видом колебательного процесса являются простые гармонические колебания, которые описываются уравнением
|
Здесь x – смещение тела от положения равновесия, xm – амплитуда колебаний, то есть максимальное смещение от положения равновесия, ω – циклическая или круговая частотаколебаний, t – время. Величина, стоящая под знаком косинуса φ = ωt + φ0 называется фазой гармонического процесса. При t = 0 φ = φ0, поэтому φ0 называют начальной фазой. Минимальный интервал времени, через который происходит повторение движения тела, называется периодом колебаний T. Физическая величина, обратная периоду колебаний, называется частотой колебаний:
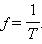 |
Частота колебаний f показывает, сколько колебаний совершается за 1 с. Единица частоты – герц (Гц). Частота колебаний f связана с циклической частотой ω и периодом колебаний T соотношениями:
|
На рис. 1.2.2 изображены положения тела через одинаковые промежутки времени при гармонических колебаниях. Такую картину можно получить экспериментально при освещении колеблющегося тела короткими периодическими вспышками света (стробоскопическое освещение). Стрелки изображают векторы скорости тела в различные моменты времени.
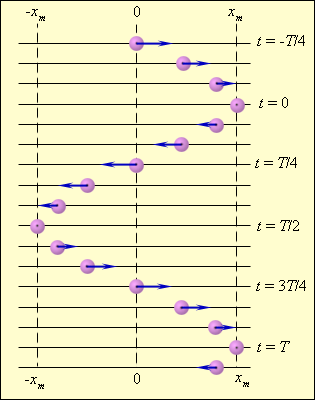 |
| Рисунок 1.2.2. Стробоскопическое изображение гармонических колебаний. Начальная фаза φ0 = 0. Интервал времени между последовательными положениями тела τ = T / 12. |
Рис. 1.2.3 иллюстрирует изменения, которые происходят на графике гармонического процесса, если изменяются либо амплитуда колебаний xm, либо период T (или частота f), либо начальная фаза φ0.
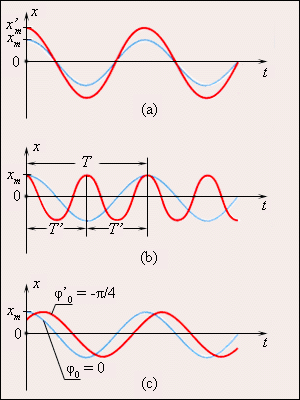 |
Рисунок 1.2.3. Во всех трех случаях для синих кривых φ0 = 0: а – красная кривая отличается от синей только большей амплитудой (x'm > xm); b – красная кривая отличается от синей только значением периода (T' = T / 2); с – красная кривая отличается от синей только значением начальной фазы ( 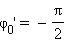 рад). рад). |
При колебательном движении тела вдоль прямой линии (ось OX) вектор скорости направлен всегда вдоль этой прямой. Скорость υ = υx движения тела определяется выражением
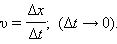 |
В математике процедура нахождения предела отношения 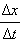 при Δt → 0 называется вычислением производной функции x(t) по времени t и обозначается как
при Δt → 0 называется вычислением производной функции x(t) по времени t и обозначается как 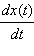 или как x'(t) или, наконец, как
или как x'(t) или, наконец, как 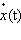 . Для гармонического закона движения
. Для гармонического закона движения 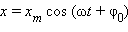 вычисление производной приводит к следующему результату:
вычисление производной приводит к следующему результату:
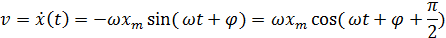 |
Появление слагаемого +π / 2 в аргументе косинуса означает изменение начальной фазы. Максимальные по модулю значения скорости υ = ωxm достигаются в те моменты времени, когда тело проходит через положения равновесия (x = 0). Аналогичным образом определяется ускорение a = ax тела при гармонических колебаниях:
 |
следовательно, ускорение a равно производной функции υ(t) по времени t, или второй производной функции x(t). Вычисления дают:
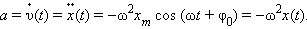 |
Знак минус в этом выражении означает, что ускорение a(t) всегда имеет знак, противоположный знаку смещения x(t), и, следовательно, по второму закону Ньютона сила, заставляющая тело совершать гармонические колебания, направлена всегда в сторону положения равновесия (x = 0).
На рис. 1.2.4 приведены графики координаты, скорости и ускорения тела, совершающего гармонические колебания.
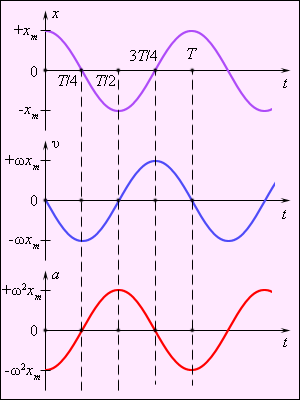 |
| Рисунок 1.2.4. Графики координаты x(t), скорости υ(t) и ускорения a(t) тела, совершающего гармонические колебания. |