Приравнивая правые части выражений (5) и (6), получаем
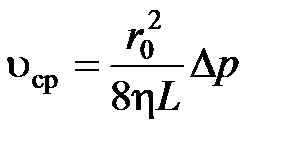 . (7)
. (7)
Сравнивая выражения (4) и (7), находим, что максимальная скорость движения частиц жидкости (газа)
 . (8)
. (8)
Из выражения (7) получаем значение динамической вязкости жидкости (газа)
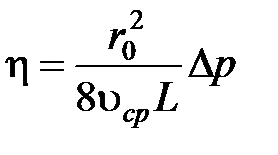
Динамическую вязкость газа можно определить и другим способом, исходя из молекулярно-кинетических представлений, согласно которым
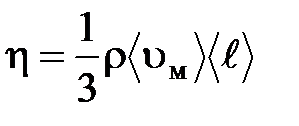 , (9)
, (9)
где 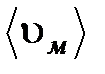 средняя скорость теплового движения молекул;
средняя скорость теплового движения молекул;  - средняя длина свободного пробега молекул;
- средняя длина свободного пробега молекул; 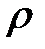 – плотность газа.
– плотность газа.
В формуле (9) и далее для скорости теплового движения молекул используется обозначение  .Это сделано для того, чтобы не путать скорости направленного движения частиц жидкости (газа) со скоростью теплового движения молекул.
.Это сделано для того, чтобы не путать скорости направленного движения частиц жидкости (газа) со скоростью теплового движения молекул.
Учет сил притяжения и отталкивания между молекулами газа приводит к более точной формуле:
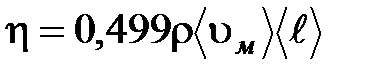 . (10)
. (10)
Значение средней скорости теплового движения молекул находится по формуле
 , (11)
, (11)
где k – постоянная Больцмана; Т – термодинамическая температура газа; m0 – масса молекулы.
Из уравнения (10) можно определить среднее значение длины свободного пробега молекул:
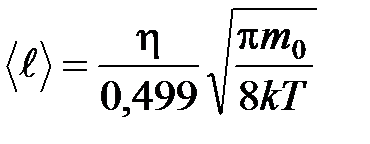 . (12)
. (12)
Значение  позволяет определить эффективный диаметр молекулы
позволяет определить эффективный диаметр молекулы
 , (13)
, (13)
где n – число молекул в единице объема.
На основании кинетической теории можно найти теоретическое приближенное значение коэффициента диффузии молекул газа
 . (14)
. (14)
Сравнивая (14) с выражением для вязкости (9), находим, что

Вводя поправку, учитывающую распределение скоростей молекул газа по закону Максвелла, получаем более точное выражение для коэффициента диффузии, который можно определить экспериментально:
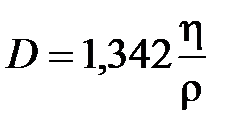 . (15)
. (15)
Таким образом, определив вязкость газа, можно найти важные газокинетические параметры: среднюю длину свободного пробега молекул 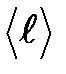 , эффективный диаметр молекулы d и коэффициент диффузии D молекул газа.
, эффективный диаметр молекулы d и коэффициент диффузии D молекул газа.
Рассмотрен случай вязкого течения газа по трубе, которое осуществляется при выполнении условия, что средняя длина свободного пробега молекул много меньше радиуса канала. При низких давлениях, когда длина свободного пробега сравнима и больше характерного размера канала, столкновения между молекулами газа будут значительно реже, чем столкновения между молекулами и стенками канала. Такое течение газа носит название "молекулярного". Существует и промежуточный тип течения. Таким образом, в зависимости от величины безразмерного параметра, называемого "числом Кнудсена", равного отношению средней длины свободного пробега молекул газа к радиусу трубы, описание течения газов через трубы разделяют на три части:
при  <0,01 течение “вязкостное”;
<0,01 течение “вязкостное”;
при  >1,00 течение “молекулярное”;
>1,00 течение “молекулярное”;
при 0,01 <  <1,00 промежуточный тип течения.
<1,00 промежуточный тип течения.
При выводе формулы Пуазейля (5) были сделаны следующие допущения:
- газ рассматривался как сплошная несжимаемая среда;
- течение полностью сформировано, т.е. распределение скоростей частиц газа по любому поперечному сечению постоянно по всей длине трубы;
- скорость частиц газа у стенки трубы равна нулю.
Чтобы установить значения этих допущений, выясним условия, при которых они становятся существенными.
Известно, что сжимаемостью газа можно пренебречь, если
 . (16)
. (16)
Здесь М – «число Маха» для течения, определяемое как отношение максимальной скорости движения частиц газа 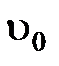 к скорости звука c в газе, которая для воздуха при комнатной температуре равна 340 м/с:
к скорости звука c в газе, которая для воздуха при комнатной температуре равна 340 м/с:

При этом труба должна быть достаточно длинной, чтобы выполнялось второе допущение, т.е. чтобы течение было полностью сформировано.
Когда газ втекает в трубу из большого объема, распределение скоростей по входному сечению приблизительно однородно. По мере прохождения газа по трубе за счет сил внутреннего трения распределение скоростей частиц газа по сечению изменяется. Расчеты показывают, что течение газа становится полностью сформированным на расстоянии  от входа в трубу
от входа в трубу
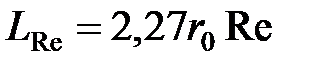
где r0 – радиус трубы; Re – «число Рейнольдса» для потока - безразмерный параметр, который определяется следующим образом:
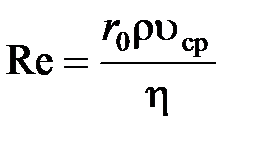 , (17)
, (17)
где ρ – плотность газа; η – динамическая вязкость; 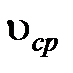 - средняя скорость движения частиц газа по сечению или скорость потока газа.
- средняя скорость движения частиц газа по сечению или скорость потока газа.
Число Рейнольдса (17) определяет отношение энергии объема газа к работе сил вязкости при движении этого объема газа. Чем меньше Re, тем большую роль играют силы вязкости в движении газа.
Число Рейнольдса является единственной безразмерной комбинацией параметров, определяющих течение вязкой жидкости (вязкого газа) по трубе. Действительно, среда полностью определяется плотностью и вязкостью, а само течение средней скоростью и радиусом канала. Такие безразмерные комбинации играют большую роль при моделировании различных явлений. В большинстве случаев моделирование процессов основано на рассмотрении физически подобных явлений. Изучение интересующего нас натурного явления мы заменяем изучением физически подобного явления, которое удобнее и проще осуществить.
Два физических явления называются подобными, если по заданным характеристикам одного можно получить характеристики другого простым пересчетом, который аналогичен переходу от одной системы единиц измерения к другой.
В теории размерности и подобия показано, что для всякой совокупности подобных явлений все соответствующие безразмерные характеристики (безразмерные комбинации размерных величин) имеют одинаковое численное значение. Верно и обратное, т.е. если все соответствующие безразмерные характеристики для движений одинаковы, то эти движения подобны. Заметим, что моделирование процессов широко применяется при проектировании самолетов, кораблей, дамб, плотин, мостов и т.д.
В зависимости от рассматриваемых явлений применяются и другие безразмерные комбинации физических параметров, например, «число Фруда», «число Струхаля», «число Прандтля» и т.д.
Вернемся к рассмотрению движения жидкости (газа) по трубе. Для всякой задачи о движении вязкой жидкости (вязкого газа) в стационарных условиях должно, в принципе, существовать точное стационарное решение уравнений гидродинамики. Эти решения формально существуют при любых параметрах среды 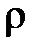 ,
, 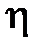 и ее течения
и ее течения 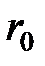 ,
,  ,но не всякое решение уравнений движения может реально существовать в природе. Осуществляющиеся в природе движения должны не только удовлетворять гидродинамическим уравнениям, а быть еще и устойчивыми: малые возмущения, раз возникнув, должны затухать со временем. Если же, напротив, возникающее в потоке возмущение стремится возрасти со временем, то движение неустойчиво и фактически существовать не может. Математическое исследование устойчивости крайне сложно. Для течения в трубе круглого сечения полное теоретическое описания устойчивости еще отсутствует.
,но не всякое решение уравнений движения может реально существовать в природе. Осуществляющиеся в природе движения должны не только удовлетворять гидродинамическим уравнениям, а быть еще и устойчивыми: малые возмущения, раз возникнув, должны затухать со временем. Если же, напротив, возникающее в потоке возмущение стремится возрасти со временем, то движение неустойчиво и фактически существовать не может. Математическое исследование устойчивости крайне сложно. Для течения в трубе круглого сечения полное теоретическое описания устойчивости еще отсутствует.
Физически переход от стационарного течения вязкой жидкости (вязкого газа) к нестационарному (неустойчивому) характеризуется чрезвычайно нерегулярным, беспорядочным изменением скорости частиц газа со временем в каждой точке потока. Такое же нерегулярное изменение скорости частиц газа имеет место от точки к точке потока, рассматриваемого в заданный момент времени.
Для всех «пуазейлевых» течений существует критическое число Рейнольдса Re, определяющее границу устойчивости или, другими словами, границу перехода от стационарного течения к турбулентному. Для трубы круглого сечения незатухающая турбулентность наблюдается уже при Re ≈ 2000. Следовательно, формула Пуазейля (5) справедлива лишь для области параметров, где Re < 2000.
Описание установки
Изучение течения воздуха через капилляр при атмосферном давлении осуществляется на установке, изображенной на рис.3.
| h | Основной частью экспериментальной установки является цилиндрическая делительная воронка 1, укрепленная на штативе. Для делительной воронки имеется несколько резиновых пробок 4, в которые вставлены трубки со стеклянными капиллярами 5, через которые атмосферный воздух может поступать в делительную воронку 1. Стеклянные капилляры имеют различные диаметры внутренних каналов. С целью увеличения механической прочности капилляры помещены в медные трубки. Сбоку, вплотную к делительной воронке 1, расположена измерительная линейка 3, которую можно перемещать вдоль делительной воронки. Под отводную трубку с краном 2 устанавливается мерный стакан. |
| Рис. 3 |
Принцип действия установки заключается в следующем: если в делительную воронку налить воды, закрыть её глухой пробкой и открыть кран, то из воронки вытечет некоторое количество воды под действием гидростатического давления и установится равновесие, при котором часть воды будет оставаться в делительной воронке. Очевидно, что в этом случае давление внутри сосуда 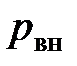 будет равно давлению атмосферного воздуха
будет равно давлению атмосферного воздуха 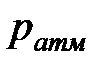 .
.
Давление 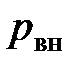 внутри сосуда будет складываться из давления
внутри сосуда будет складываться из давления  над водой и давления
над водой и давления 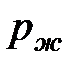 столба воды высотой h от крана 2 до поверхности воды в делительной воронке 1. Условие равновесия можно записать в виде
столба воды высотой h от крана 2 до поверхности воды в делительной воронке 1. Условие равновесия можно записать в виде
 , (18)
, (18)
где  ;
;  – плотность воды;
– плотность воды;  – ускорение свободного падения.
– ускорение свободного падения.
Если теперь глухую пробку заменить пробкой с капилляром, то равенство (18) станет динамическим, т.е. оно будет выполняться в каждый момент времени при 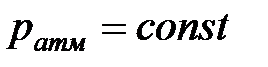 , но с течением времени величины
, но с течением времени величины  и
и  будут меняться.
будут меняться.
Действительно, из (18) следует, что на концах капилляра существует разность давлений

вызывающая течение воздуха по капилляру. Объем атмосферного воздуха, поступающего в делительную воронку за время 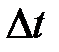 ,равен объему воды, вытекающей за это время из делительной воронки. При этом уменьшается высота h столба воды и давление
,равен объему воды, вытекающей за это время из делительной воронки. При этом уменьшается высота h столба воды и давление  . Соответственно изменяется и давление
. Соответственно изменяется и давление  , но уравнение (18) всегда время выполняется.
, но уравнение (18) всегда время выполняется.
Допустим, что первоначальная высота столба воды была  , а через промежуток времени
, а через промежуток времени 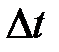 эта высота стала равной
эта высота стала равной  . В начальный момент времени на концах капилляра разность давлений воздуха была равна
. В начальный момент времени на концах капилляра разность давлений воздуха была равна
 ,
,
по истечению времени 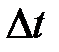

Если объем вытекающей воды достаточно мал, а диаметр делительной воронки велик, изменение высотыстолба воды будет небольшим, и можно принять, что течение воздуха по капилляру за время наблюдения 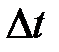 происходит при постоянной средней разности давлений на концах капилляра
происходит при постоянной средней разности давлений на концах капилляра
 , (19)
, (19)
где 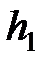 и
и  - высоты столба жидкости, соответственно, в начале и в конце наблюдения;
- высоты столба жидкости, соответственно, в начале и в конце наблюдения;  - плотность воды;
- плотность воды;  – ускорение свободного падения.
– ускорение свободного падения.
Порядок выполнения работы
1. Закрыть кран делительной воронки и налить в неё воду до уровня 250-320 мм.
2. Вставить плотно в горло делительной воронки пробку с капилляром так, чтобы нижний конец капилляра не касался воды.
3. Поставить под делительную воронку любую емкость объемом 100 -200 мл и открыть кран. После того, как течение воды стабилизируется, можно приступить к измерениям.
4. Заменить емкость под делительной воронкой на мерный стакан и одновременно включить секундомер. В этот же момент времени отметить высоту водяного столба h1 по линейке и записать в табл.1.
5. Спустя промежуток времени Δt = 10 мин перекрыть кран воронки и выключить секундомер. Отметить высоту водяного столба h2 по линейке. Результат измерения записать в табл.1.
6. Измерить температуру T и давление 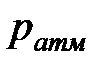 в помещении и записать в табл.1.
в помещении и записать в табл.1.
7. По измеренному объему 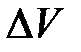 воды, вытекшей из делительной колонки в мерный стакан за время Δt, определить среднюю скорость движения частиц воздуха или скорость потока воздуха в капилляре:
воды, вытекшей из делительной колонки в мерный стакан за время Δt, определить среднюю скорость движения частиц воздуха или скорость потока воздуха в капилляре:
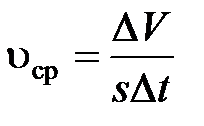
где 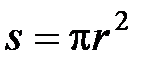 – площадь поперечного сечения капилляра.
– площадь поперечного сечения капилляра.
8. Вычислить максимальную скорость 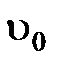 частиц воздуха по формуле (8).
частиц воздуха по формуле (8).
9. Вычислить среднее значение разности давлений  воздуха на концах капилляра по формуле (19), принимая
воздуха на концах капилляра по формуле (19), принимая 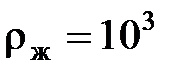 кг/м3 и
кг/м3 и 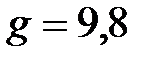 м/с2. Результат расчета занести в табл.1.
м/с2. Результат расчета занести в табл.1.
9. Определить динамическую вязкость 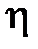 воздуха по формуле
воздуха по формуле
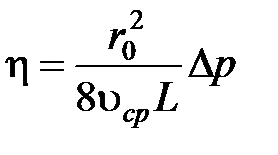
где 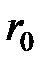 – радиус;
– радиус;  – длина капилляра. Результат расчета записать в табл.1.
– длина капилляра. Результат расчета записать в табл.1.
10. Вычислить среднюю скорость теплового движения молекул 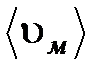 по формуле (11) и среднюю длину свободного пробега
по формуле (11) и среднюю длину свободного пробега  молекул воздуха по формуле (12), принимая среднюю молярную массу воздуха М = 0,029 кг/моль.
молекул воздуха по формуле (12), принимая среднюю молярную массу воздуха М = 0,029 кг/моль.
11. Найти эффективный диаметр d молекулы воздуха по формуле (23), предварительно вычислив число молекул воздуха в единице объема по формуле 
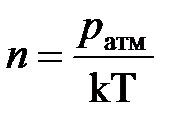
12. Вычислить плотность атмосферного воздуха по формуле

где R – универсальная газовая постоянная. Результаты расчетов занести в табл.1.
13. Рассчитать теоретическое и экспериментальное значения коэффициент диффузии молекул воздуха по формулам (14), (15) и занести в табл.1.
14. Найти число Маха M по формуле  . Используя неравенство
. Используя неравенство  определить возможность пренебрежения сжимаемостью воздуха при его течении в данных условиях.
определить возможность пренебрежения сжимаемостью воздуха при его течении в данных условиях.
16. Найти число Рейнольдса Re по ормуле (17). Сравнить полученное число Re со значением 2000 и установить: является ли течение воздуха стационарным, либо турбулентным.
Таблица 1
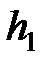 , м , м | 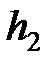 , м , м | T, K |  , Па , Па |  , м3 , м3 | 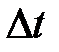 , с , с | 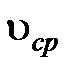 , м/с , м/с | 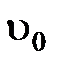 , м/с , м/с | 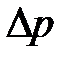 , Па , Па |
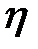 , Па·с , Па·с | d, м | 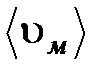 , м/с , м/с |  , м , м | 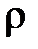 , кг/м3 , кг/м3 |  , м2/c , м2/c |  , м2/c , м2/c | M | Re |
18. Сравнить экспериментально рассчитанные значения физических величин 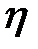 , d,
, d,  ,
, 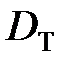 ,
,  со значениями соответствующих величн, приведенных в табл. 2. Оценить степень расхождения сравниваемых физических величин.
со значениями соответствующих величн, приведенных в табл. 2. Оценить степень расхождения сравниваемых физических величин.
19. По найденному числу Рейнольдса Re для течения воздуха через капилляр определить разность давлений на концах трубки длиной L = 150 мм и радиусом  мм при течении через нее воды, используя формулу
мм при течении через нее воды, используя формулу
 .
.
Таблица 2
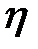 , Па·с , Па·с | d, м |  , м , м | D, м2/c |
| 1,81·10-5 | 3,74·10-10 | 6,7·10-8 | 1,7·10-5 |
Контрольные вопросы
1. При каких условиях жидкость и газ можно объединить одним термином «жидкость»?
2. Какое течение называется вязким?
3. Каков механизм внутреннего трения?
4. Что называется средней длиной свободного пробега молекулы?
5. Какие допущения принимаются при выводе формулы Пуазейля?
6. Что определяет число Маха?
7. Для чего используется число Рейнольдса?
8. Какие явления называются физически подобными?
9. Какое течение называется турбулентным?
ЛАБОРАТОРНАЯ РАБОТА №9
