Определение коэффициента самоиндукции катушки и емкости конденсатора

Цель работы:1)определение индуктивности катушки без сердечника и с сердечником; 2)определение емкости конденсатора;3)наблюдение явления резонанса.

Приборы и принадлежности: исследуемая катушка с сердечником, вольтметр, амперметр, реостат, источник переменного тока.

Теоретическое введение

Если в проводнике изменяется сила тока, то в нем возникает ЭДС самоиндукции, препятствующая этому изменению. ЭДС самоиндукции пропорциональна изменению силы тока в единицу времени:

e = -L 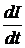. (1)

Коэффициент пропорциональности L называется коэффициентом самоин­дукции и зависит от формы и размеров проводника и от магнитной прони­цаемости окружающей среды. Если предположить e = 1 В, dI/dt =1 А/с, то L = 1 Гн (Генри). Таким образом, самоиндукцией в 1 Гн обладает такой проводник, в котором изменение силы тока со скоростью 1 А в 1 сек вы­зывает ЭДС самоиндукции в 1 В. У линейных проводников коэффициент са­моиндукции мал. Большими коэффициентами самоиндукции обладают, так называемые, катушки индуктивности, состоящие из большого числа витков. Пусть сопротивление постоянному току проволоки, из которой намотана катушка, равно R. Это сопротивление часто называют активным. Если включить такую катушку в цепь переменного тока, то в следствии периоди­ческого изменения силы тока возникает ЭДС индукции, препятствующая приложенному напряжению. Это приводит к тому, что сопротивление катушки становится больше, чем активное. Иначе говоря, катушка индуктивности будет обладать не только активным, но и индуктивным (реактивным) сопротивлением X_L.

Если в цепь переменного тока включен конденсатор С, то вследствие периодического изменения направления тока происходит его перезарядка, что приводит к появлению емкостного сопротивления X_C.

Рассмотрим цепь, состоящую из последовательно соединенных сопротивления R, индуктивности L,

и конденсатора С (рисунок 1).

По второму закону Кирхгофа для

замкнутого контура сумма падений

напряжений равна сумме электро- Рисунок 1

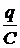движущих сил

I R + = e_оsinwt - L 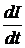. (2)

Для установившегося режима колебаний решение этого уравнения име­ет вид:

I =I_o sin (wt - j), (3)

где j - разность фаз между приложенной ЭДС и силой тока.

Расчет приводит к следующим значениям амплитуды тока

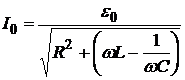, (4)

разности фаз между током и внешней ЭДС.

tgj = ,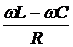

где 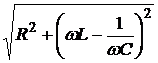= Z - полное сопротивление цепи переменного тока,

X_L = wL - индуктивное сопротивление; X_C = 1/wC - емкостное сопро­тивление.

В выражении (4) фигурируют амплитудные (максимальные) значения тока - I_o и ЭДС -e₀. На практике обычные вольтметры и амперметры по­казывают не максимальные, а так называемые эффективные (или действую­щие) значения I_эфф, U_эфф и e_эфф, следовательно

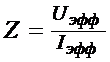, (5)

где Iэфф = 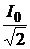; Uэфф = 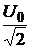; тогда = .

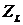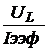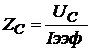. (5 а,б)

Если цепь состоит из источника ЭДС и емкости т.е. (R=0, L=0), то

,

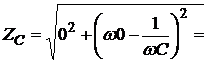
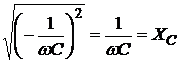откуда

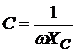. (6)

Таким образом, электрическая емкость C обратно пропорциональна круговой частоте переменного электрического тока

w = 2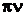 ,(7)

где n = 50 Гц, и емкостному сопротивлению Х_с.

Если емкостное сопротивление равно нулю (Х_с = 0),то

,

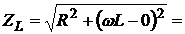
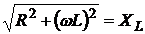откуда

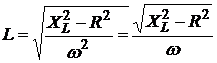. (8)

Таким образом, для определения коэффициента самоиндукции катушки необходимо знать ее сопротивление Х_L, омическое сопротивление R и круговую частоту переменного тока w. R = 16 Ом.

Порядок выполнения работы

Для определения индуктивности катушки и емкости конденсатора ис­пользуем установку, схема которой показана на рисунке 2.

Рисунок 2

1. Ознакомиться с установкой.

2. Тумблером "К" включить установку.

3. Изменяя напряжение с помощью потенциометра для 3-х значений тока I₁,I₂,I₃, записать в отчетную таблицу показания V_L, V_C, V.

4. Вставить в катушку полностью сердечник и повторить те же изме­рения и занести их в таблицу.

5. По формулам (5 а,б) рассчитать индуктивное сопротивление Х_L и емкостное сопротивление Х_C.

6. По формуле (8) вычислить индуктивность катушки без сердечника и с сердечником. Найти среднее значение.

7. По формуле (6) вычислить емкость конденсатора.

8. Путем постепенного введения сердечника в катушку по максималь­ному показанию амперметра и показаниям вольтметров добиться резонанса. Показания приборов занести в таблицу.

Таблица измерений

	Индуктивность катушки	Емкость конденсатора
	Iэфф. (А)	Uоб. (В)	UL (В)	XL (Ом)	L (Гн)	Lср. (Гн)	UС (В)	XС (Ом)	C (Ф)	Cср. (Ф)
Без сердечника
С сердечником
Резонанс

Контрольные вопросы

1.Какой ток называется переменным? Записать уравнения для переменного тока и напряжения, пояснить каждый член уравнения.

2.Какие ток и напряжение называются эффективными и как они связаны с амплитудными значениями? Выяснить физический смысл.

3.Записать формулу емкостного сопротивления.

4.В чем заключается явление самоиндукции? Напишите формулу ЭДС самоиндукции.

5.Что называется индуктивностью катушки, от чего она зависит, каков ее физический смысл?

6.Записать формулу и выяснить физический смысл индуктивного сопротивления.

7.Записать и сформулировать закон Ома для цепи переменного тока, состоящей из Х_L, Х_С, R. Чему равно полное сопротивление в отсутствии резонанса и при резонансе?

8. Представить сдвиг фаз между током и напряжением для Х_L, Х_C графически и с помощью векторной диаграммы. Чему равна разность фаз между током и напряжением.

ЛАБОРАТОРНАЯ РАБОТА

ОПРЕДЕЛЕНИЕ РАДИУСА КРИВИЗНЫ ЛИНЗЫ

ПО КОЛЬЦАМ НЬЮТОНА

Приборы и принадлежности: измерительный микроскоп, осветитель, светофильтр, линза, пластинка из стекла.

Теоретическое введение

Одним из доказательств волновой природы света является интерференция световых волн. Она может наблюдаться только для когерентных волн.

Световые волны, имеющие равные длины волн (частоты) и колеблющиеся в одинаковых фазах или с постоянной разностью фаз, называются когерентными. Наложение таких волн друг на друга приводит к суммированию интенсивностей, амплитуд колебаний и образованию максимумов и минимумов.

Явление интерференции широко используется для практических и научных целей. Рассмотрим одно из применений интерференции света.

Если на плоскую, хорошо отполированную, пластинку положить выпуклую линзу с поверхностью очень малой кривизной и направить нормально к поверхности пластинки пучок монохроматических лучей, то в отраженном свете в месте соприкосновения линзы и пластинки явственно видно круглое черное пятно, а вокруг него ряд концентрических светлых и темных колец. Рассматривая ход лучей через линзу, в проходящем свете наблюдается обратная картина: в центре – светлое круглое пятно, вокруг – ряд чередующихся светлых и темных колец. При этом все светлые кольца будут видны в проходящем свете на тех же местах, где в отраженном размещались темные и наоборот.

При пользовании белым светом в центре наблюдается темное пятно в отраженном свете, белое – в проходящем, окруженное рядом цветных колец всех оттенков радуги.

Явление это было впервые описано современником Ньютона – Р.Гуком. Ньютон же подробно исследовал его и установил связь между радиусом колец и радиусом линзы, почему это явление и получило название «колец Ньютона».

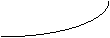
Возникновение колец Ньютона объясняется интерференцией световых вол, отраженных от верхней и нижней поверхностей воздушной прослойки между линзой и плоской пластинкой. (рисунок 1)

О

S₁ S₂ R

А r_m

В C d

D B

Рисунок 1 Рисунок 2

На линзу падает пучок плоских монохроматических световых волн. Часть пучка S_1, пройдя линзу, воздушную прослойку АВ и отразившись от плоской стеклянной пластинки в точке В, пройдет по пути ВСО. Другая часть пучка S₂, пройдя линзу и отразившись от поверхности воздушной прослойки в точке С, пройдет линзу в направлении СО. Направления рассматриваемых лучей от точки С будут совпадать. Это совпадение будет тем больше, чем ближе направления падающих на линзу лучей и нормали и чем больше радиус кривизны. Тогда можно считать, что АВ=ВС. В точке С лучи, налагаясь друг на друга, будут интерферировать, что приведет к образованию системы концентрических темных и светлых колец Ньютона.

Для количественной оценки интерференции нужно знать разность хода, образовавшегося между двумя лучами:S₁ABCO и S₂CO до точки С. Разность хода есть то расстояние, на которое одна волна обгоняет (или отстает) от другой. Если толщина воздушной прослойки в точке С равна d, а АВ=ВС, то геометрическая разность хода лучей будет равна АВ+ВС = 2d .

Однако, для получения выражения для оптической разности хода между лучами в точке С необходимо еще учесть весьма важное обстоятельство. Световые волны, как и всякие волны, отражаясь от более плотной среды «теряют полволны», т.е. испытывают изменение фазы. В нашем случае первый луч S₁AB отражается от более плотной среды, и второй S₂ - от менее плотной среды. Следовательно, между ними образуется дополнительная разность хода l /2. Тогда полная разность хода D равна

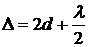. (1)

Зная оптическую разность хода, запишем условие минимума в интерференционной картине.

D=(2m+1)l¤2; m=0, 1, 2, 3….

В тех местах воздушной прослойки d , где разность хода равна нечетному числу полуволн, образуются темные кольца. Это условие можно записать в следующем виде

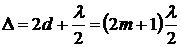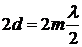или . (2)

При m = 0 будет центральное черное пятно, при m = 1, 2, 3, … соответственно первое, второе и т.д. темные кольца Ньютона.

Аналогично условие максимума, где образуются светлые концентрические кольца, будут в тех местах, для которых разность хода равна четному числу полуволн

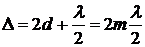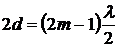, , (3)

где m =1. 2. 3… номер светлых колец.

Выразим зависимость воздушного зазора d через радиус темного кольца r_m и радиус кривизны R. Из рисунка 2 имеем 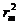=R²-(R-d)²=2Rd-d². Принимая во внимание, что 2R>>d, можно пренебречь величиной в сравнении с 2R, тогда получим

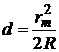. (4)

Из этой, а также (1) зависимостей становится понятным, почему при удалении от центра к периферии линзы кольца Ньютона делаются все уже и располагаются чаще. Объясняется это тем, что d (а следовательно и D) растет пропорционально r 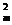, и угол клина соответствующий каждому кольцу резко возрастает. Если подставить в (4) значение (2) для величины воздушной прослойки d_m тех мест, где образуются темные кольца Ньютона, то можно найти радиус кривизны линзы

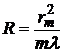. (5)

Из формулы(5), если известна длина световой волны, которой освещается пластинка с линзой, и с помощью микроскопа измерен радиус r_m - темного кольца, можно определить радиус кривизны линзы. Такой способ определения особенно удобен при больших значениях R.

В настоящей работе с целью уменьшения погрешностей в результатах измерений применен метод, при котором в поле зрения микроскопа измеряется разность диаметров двух темных колец D_n - D_m, причем берутся кольца не расположенные рядом, т.е.n-m>2.Тогда применяя (5), для 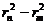имеем

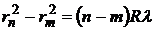, (6)

из выражения (6) получаем рабочую формулу для определения радиуса кривизны линзы

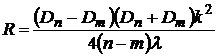. (8)

Порядок выполнения работы

1. Включить осветитель в сеть и небольшими поворотами стеклянной пластины и перемещениями осветителя добиться наиболее яркого освещения поля зрения.

2. Осторожно перемещать пластинку с линзой по столику микроскопа до тех пор, пока в поле зрения не появятся кольца. Добиться такого положения колец, чтобы их диаметры расположились вдоль шкалы, а центр – вблизи середины шкалы. Плавно перемещая тубус, получить наиболее резкое изображение колец.

3. Произвести измерение диаметров колец. Каждое кольцо измерить не менее 3 раз и средний результат записать в таблицу. В виду того, что кольца имеют заметную ширину, следует брать отсчет соответствующий середине кольца.

4. По формуле (8) из различных соотношений диаметров колец определить не менее 5 значений радиуса кривизны линзы R.Для уменьшения погрешностей результата следует брать n-m³2.

5. Рассчитать погрешности и дать окончательный результат для радиуса кривизны линзы в виде R=R±DR.

Таблица измерений

Длина волны осветителя l	Цена деления шкалы к	Средние диаметры колец (в делениях шкалы)
Д1	Д2	Д3	Д4	Д5	Д6	Д7	Д8

ЛАБОРАТОРНАЯ РАБОТА

ОПРЕДЕЛЕНИЕ ДЛИНЫ СВЕТОВОЙ ВОЛНЫ С ПОМОЩЬЮ ДИФРАКЦИОННОЙ РЕШЕТКИ

Цель работы: Определение длин волн красного, зеленого и фиолетового лучей для четко видимых спектров 1-го и 2-го порядков.

Приборы и принадлежности: Дифракционная решетка, экран, лампа для подсвечивания.

Теоретическое введение

Если пучок параллельных лучей света встречает на своем пути непрозрачное круглое тело или его пропускают через достаточно малое круглое отверстие, то на экране будет замечено светлое или темное пятно в центре чередующихся темных и светлых колец.

Это явление распространения света в область геометрической тени, указывающее на отступление от закона прямолинейности распространения света получило название дифракции света.

Для получения ярких дифракционных спектров применяются дифракционные решетки. Дифракционная решетка представляет собой плоскую стеклянную пластинку, на которой с помощью делительной машины нанесен ряд параллельных штрихов (в хороших решетках - до 1000 штрихов на миллиметр). Штрихи являются практически непрозрачными для света, т.к. из-за своей шероховатости они в основном рассеивают свет. Промежутки между штрихами свободно пропускают свет и называются щелями.

Совокупность ширины штриха и прозрачного промежутка называется периодом или постоянной решетки. Если обозначить ширину штриха через b, а ширину щели а, то период решетки

d = a +b.

Пусть на решетку падают лучи света перпендикулярно плоскости. Свет, проходя через каждую щель, испытывает дифракцию, т.е. отклоняется от прямолинейного направления. Если на пути лучей, распространяющихся от щелей решетки, поместить линзу, а в фокальной плоскости линзы экран, то на экране в одну точку соберутся все параллельные лучи, идущие под одним и тем же углом к нормали (рисунок 1). Лучи идущие под другим углом, соберутся в другой точке. Освещенность каждой точки экрана будет зависеть как от интенсивности света, даваемой каждой щелью в отдельности, так и от результата интерференции лучей, прошедших через разные щели Как видно из рисунка 1 разность хода лучей для двух соседних щелей

∆ = d sin ,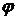

где d -период решетки, φ - угол отклонения лучей.

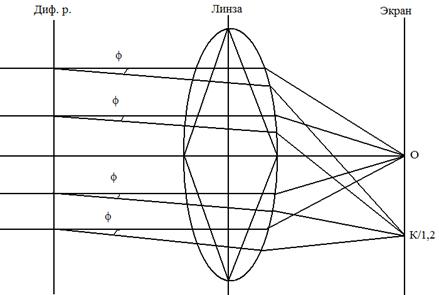
Рисунок 1

Если эта разность будет равна четному числу полуволн, в направлении угла φ будет наблюдаться максимум освещенности:

d sinφ = 2kλ/2 = kλ, (1)

а при условии

d sinφ = (2k+1)λ/2 (2)

наблюдается минимум.

Легко видеть, что при разности хода ∆=kλ все остальные щели будут по направлению угла φ также давать максимум, т.к. во всех случаях разности хода будут кратны. Эти максимумы называются основными.

Итак, при нормальном падении лучей на решетку для основных максимумов, полученных на экране от дифракционной решетки, имеем соотношение:

d sinφ = kλ, (3)

где k - 1,2,3 ,…целое число, называемое порядком спектра. Понятие порядок спектра связано с тем, что на экране наблюдается ряд максимумов, симметрично расположенных относительно белой полосы (спектр нулевого порядка), образованной светом, прошедшим через решетку без отклонения.

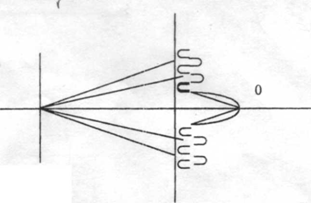
Из формулы (3) видно, что чем больше длина волны, тем большему углу дифракции соответствует положение максимума (рисунок 2). При падении на решетку монохроматического света на экране возникают одноцветные полосы. Формула (3) позволяет определить длину световой волны:

λ=d sinφ/k. (4)

Рисунок 2

Определение длины волны сводится к измерению угла φ. Для измерения углов служит специальный прибор гониометр (рисунок 3). Где К - каллиматор со щелью (для получения узкого пучка параллельных лучей); Т - зрительная труба; ОК – окуляр с нитью для наведения трубы на определенную линию спектра; С - круговая шкала с нониусом;

Др - дифракционная решетка.

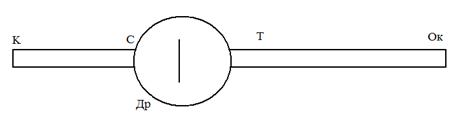
Рисунок 3

Порядок выполнения работы

1.Устанавливают зрительную трубу так, чтобы нить окуляра совпадала с неокрашенным изображением щели (спектр нулевого порядка) и проводят отсчет положения трубы по шкале. Это положение является нулевым положением трубы по шкале φ₀.

2.Трубу поочередно наводят на различные линии спектра 1-го и 2-го порядков сначала в одну, а затем в другую сторону от нулевого положения. Для всех линий определяют угол отклонения φ_л; φ_пр:

, .

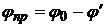
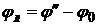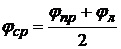Таблица измерений

		отсчеты		длина
порядок спектра	цвет спектра	нач. полож. φ0	вправо φ’	влево φ"	вправо φ1	влево φ2	φср	sin φср	волны λ 10-7 м
к = 1	фиолет. зеленый красный
к = 2	фиолет. зеленый красный

Порядок (период) дифракционной решетки d = 10⁵ м.

Контрольные вопросы

1.В чем заключается явление дифракции?

2.При каком условии наблюдается дифракция?

3.Условие главного максимума интенсивности света при дифракции на дифракционной решетке.

4.Что называется постоянной дифракционной решетки?

5.Почему белый свет разлагается на спектр при прохождении через дифракционную решетку?

6.В чем заключается метод зон Френеля?

ЛАБОРАТОРНАЯ РАБОТА