Определение коэффициента вязкости воздуха, средней длины свободного пробега и эффективного диаметра молекул
Оборудование: аспиратор, манометр, мензурка, секундомер.
Теоретическое введение
Молекулярно-кинетическая теория позволила получить формулы, связывающие макроскопические параметры газа (давление, объем, температура) с его микроскопическими параметрами ( размеры и масса молекулы, ее скорость, средняя длина свободного пробега молекул). Пользуясь этими формулами на основании измеренных параметров газа можно найти его микроскопические параметры.
Для нахождения средней длины свободного пробега можно воспользоваться формулой, выражающей зависимость коэффициента внутреннего трения газа η отλ и υ:
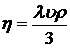 , (1)
, (1)
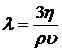 , (1а)
, (1а)
где: ρ - плотность газа, υ - средняя арифметическая скорость молекул газа равна:
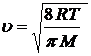 (2)
(2)
здесь R= 8,31 Дж/моль∙К газовая постоянная, Т - абсолютная температура газа, М - молярная масса газа. Плотность ρ газа можно найти из уравнения Клапейрона-Менделеева.
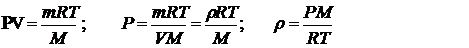 (3)
(3)
здесь: Р- давление газа при данных условиях.
Коэффициент вязкости можно определить, пользуясь законом Пуазейля. Исходя из которого коэффициент вязкости газа η зависит от параметров капиллярной трубки, через которую проходит газ, и разности давлений ΔP, поддерживаемой на концах этой трубки, т.е.:
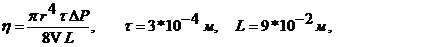 (4)
(4)
где: r - радиус, L - длина трубки, V - объем газа, проходящего через трубку за время τ, ΔP - разность давлений на концах трубки.
Подставляя выражения (4),(3) и (2) в формулу (1а), получим
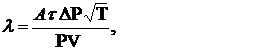 (5)
(5)
где:
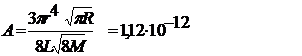 (6)
(6)
некоторая постоянная
Эффективный диаметр молекулы можно определить из формулы, выражающей зависимость средней длины свободного пробега молекулы от концентрации молекул n и эффективного диаметра молекулы dэф
 (7)
(7)
По основному уравнению молекулярно-кинетической теории газов
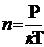 , (8)
, (8)
где:Р - давление газа (атмосферное давление); n - концентрация молекул
воздуха; k=1,38∙10-23 Дж/K - постоянная Больцмана.
Из формул (7),(8) получаем:
 (9)
(9)
Для проведения измерения собираем установку состоящую из аспиратора, из него начнет выливаться вода, давление в нем понижается, через капилляр и осушительный фильтр в него засасывается воздух.
Вследствие внутреннего трения, давление на концах не одинаково, что фиксируем манометр. Объем прошедшего через капилляр воздух за время t равен объему вылившейся из аспиратора воды, которой измеряется мензуркой.
Порядок выполнения работы
1. Наполняют баллон аспиратора водой. Осторожно открывают кран аспиратора так, чтобы вода из него текла тонкой струей, давление в нем понижается, через капилляр и осушительный фильтр в него засасывается воздух. Через некоторое время установится стационарное течение и манометр покажет некоторую постоянную разность на концах трубки. Записывают показание манометра в таблицу и определяют разность делений:
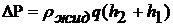 ,
,
здесь: ρжид - плотность жидкости в манометре, q- ускорение свободного падения, (h2+ h1) - разность высот столбов жидкости в манометре.
2. Подставляют под струю мензурку и замеряют время t с помощью секундомера, в течение которого вытекает объем жидкости 50 - 100 см3.
Объем прошедшего через капилляр воздуха за это время равен объему вылившейся из аспиратора воды.
3. Опыт повторяют еще два раза при различных истечениях воды.
Результаты заносят в таблицу.
4. По формулам (5) и (4) рассчитывают λ и η. По формуле (9) определяют dэф.
5. Полученные результаты сравнивают с табличными значениями.
Таблица измерений
| N n/n | P (Па) | Т (К) | h1 (мм) | h2 (мм) | DP (Па) | t (с) | V (м3) | h Па*с | l (м) | dэф (м) |
| cр. |
Контрольные вопросы
1. Основные положения МКТ и их опытное обоснование.
2. Основное уравнение МКТ газов.
3. Скорость молекул идеального газа.
4. Средняя длина свободного пробега молекул.
5. Внутреннее трение (вязкость) в газах. Коэффициент внутреннего трения.
6. Закон Пуазейля.
ЛАБОРАТОРНАЯ РАБОТА
