Фазовые равновесия. Фазовые превращения. Однокомпонентные системы.

Глава 3

Фазовые равновесия. Фазовые превращения. Однокомпонентные системы.

Введение. Основные понятия.

Фаза – это часть системы, одинаковая во всех точках по химическому составу и физическим свойствам и отделённая от других гомогенных частей системы поверхностями раздела.

Поскольку газы полностью смешиваются друг с другом, в системе может быть только одна газовая фаза, но много твердых и несколько жидких фаз.

Для каждой фазы чистого вещества связь между P,V и T выражается уравнением состояния.

Сочетание фаз в случае чистых веществ разнообразны, но их можно предсказывать и систематизировать с помощью термодинамики.

Термодинамика даёт правило фаз и уравнение Клапейрона для фазовых переходов чистого вещества. Термодинамика не отвечает на вопрос, при какой температуре будет происходить тот или иной переход.

Критерий обратимости и необратимости полиморфных превращений.

Если эта Т₁ лежит выше Т_П перехода кристаллических модификаций, то их превращения являются энантиотропными.

Действительно, T₁>T₂>T_П (см. рисунок).

Ниже T<T_П устойчива сера ромбическая, при Т>Т_П устойчива сера моноклинная.

Если точка пересечения кривой давления насыщенных паров кристаллических модификаций лежит ниже их T перехода, то он будет монотропен.

Примером являются модификации фосфора.

Белый P_I и белый P_II могут энантиотропно переходить один в другой, но обе эти модификации монотропно переходят в фиолетовый фосфор.

Правило фаз

В 1876 году Гиббс вывел простую формулу, связывающую число фаз, находящихся в равновесии, число компонентов и число независимых интенсивных переменных, необходимых для полного описания состояния системы.

Определение:

с-число компонентов в системе - это наименьшее число веществ, с помощью которых можно описать состав любой фазы системы в отдельности, S_опт=с.

S – число веществ , совокупность которых образует систему.

Всегда с<S, т.к. концентрации различных веществ при равновесии могут быть связаны определёнными соотношениями, => нет необходимости использовать для описания системы концентрации всех S веществ.

Существует два типа связи: уравнение химического равновесия и начальные условия.

Для любой отдельной химической реакции число независимых концентраций при равновесии уменьшается на единицу.

Например:

H₂O=H₂+1/2O₂

Пусть молекулярный водород и молекулярный кислород, находящиеся в равновесии с водой, тогда существует не больше двух независимых компонента (H₂O и O₂; H₂O и H₂; H₂ и O₂), т.к.концентрация третьего компонента определяется константой равновесия:

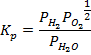
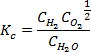
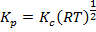
P=CRT

P_i – парциальные давления различных газов; C_i – число молей газа в литре.

Если указаны нормальные условия, то число компонентов уменьшается ещё на один, т.е. до единицы.

Например, если H₂ и O₂ образуются только из воды, то существует дополнительное уравнение:

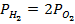
Число компонентов выражается:

C=S-n-m,

Где S-число веществ; n – число независимых химических реакций; m – число соотношений между концентрациями, определённых нормальными условиями.

Выбор компонентов произволен, но число их является важной характеристикой системы.

Определение:

Число степеней свободы – наименьшее число независимых переменных (P,T, концентраций веществ во всех фазах), которые необходимо задать, чтобы полностью описать состояние системы.

Пример:

Пусть количество газа фиксировано, как видели ранее, для описания его состояния необходимо определить только две переменные (T и P; P и V; V и T). Третью компоненту можно рассчитать из уравнения состояния f(P,V)=θ. Таким образом чистый газ имеет две степени свободы.

Рассмотрим равновесную систему из p-фаз:

P-число различных типов фаз (в тройной точке воды – 3 фазы).

Видели:

Если фаза содержит «с» компонентов, то её состав можно описать с помощью с-1 концентраций. Концентрацию одного любого компонента можно найти из соотношения

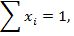
Где x_i – мольная доля i компонента.

Следовательно, общее число концентраций, которое характеризует систему равно (с-1) для каждой из p фаз, т.е. всего (с-1)p.

Кроме того, нужно ещё рассмотреть T и P и поэтому общее число независимых переменных (T+P)= (с-1)p+2.

Понятно, что учитывать T,P для каждой фазы в отдельности не нужно, т.к. фазы находятся в равновесии.

Если один из параметров поддерживается постоянным, то число независимых переменных (с-1)p+1

Если система находится в поле воздействия сил магнитного поля, то число независимых переменных (с-1)p+3

Рассмотрим условия равновесия:

Мы знаем , что в этих условиях должны выполняться определённые соотношения.

Например:

μ всех компонент во всех фазах один и тот же.

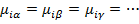
Число фаз: (α,β,γ…)=p

Для любого компонента количество равновесных состояний p-1.

Например, при наличии двух фаз существует лишь одно равновесное состояние для любого компонента.

Если число компонентов с, каждый из которых равновесно распределён между фазами, то общее количество равновесных состояний c(p-1).

Тогда:

число степеней свободы = общее число переменных – общее количество равновесных состояний между этими переменными.

Другими словами

v - дополнительное число переменных, которые должны быть заданы для полного определения состояния системы.

Для систем, с которыми мы имеем дело переменными являются T, P, концентрация:

v=[p(c-1)+2]-c(p-1),

с - число компонентов,

p - число фаз (все фазы находятся в равновесии).

v=c-p+2 - Правило фаз Гиббса

(3.3)

Выводы:

Чем больше компонентов в системе, тем больше степеней свободы.

Чем больше фаз, тем меньше переменных (T, P, концентрация) необходимо определить для полного описания системы.

Для каждого числа компонентов число фаз максимально, когда v=0 (система называется инвариантной).

Для однокомпонентной системы максимальное число фаз p: при равновесии p=c-v+2=1+0+2=3.

[Пример - тройная точка воды существует при единственном сочетании T=0,01⁰C и P=4,58 мм.рт.ст]

Првило фаз для однокомпонентной системы:

v=3-p

(3.3)

Таблица

p	v	Название системы	Переменные
		бивариантна	Одна фаза, например, водяной пар, то нужно определить T и P
		моновариантна	2 фазы: водяной пар в равновесии с жидкой водой. Необходимо определить либо Т, либо P, т.к. для данной T существует только одно равновесное P и наоборот.
		инвариантна	Сосуществование трёх фаз возможно при единственном сочетании T и P

Глава 3

Фазовые равновесия. Фазовые превращения. Однокомпонентные системы.

Введение. Основные понятия.

Фаза – это часть системы, одинаковая во всех точках по химическому составу и физическим свойствам и отделённая от других гомогенных частей системы поверхностями раздела.

Поскольку газы полностью смешиваются друг с другом, в системе может быть только одна газовая фаза, но много твердых и несколько жидких фаз.

Для каждой фазы чистого вещества связь между P,V и T выражается уравнением состояния.

Сочетание фаз в случае чистых веществ разнообразны, но их можно предсказывать и систематизировать с помощью термодинамики.

Термодинамика даёт правило фаз и уравнение Клапейрона для фазовых переходов чистого вещества. Термодинамика не отвечает на вопрос, при какой температуре будет происходить тот или иной переход.