Векторное поле и способы его изучении с помощью векторных линий

Векторное поле определяется векторной функцией точки

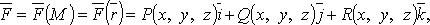
где 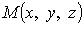- точка пространства, 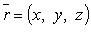- ее радиус-вектор.

Векторная линия (силовая линия, линия тока) поля - решение системы

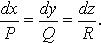
40. Формула Стокса её приложение к вычислению поверхностных интегралов

Известно, что формула Грина сводит двойной интеграл по плоской области D к криволинейному интегралу по контуру L , ограничивающему область D

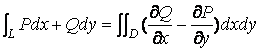( 16 )

Эта формула легко обобщается на случай, когда вместо куска плоской поверхности D берется кусок произвольной гладкой двухсторонней поверхности G , ограниченной контуром L. Формула Стокса :

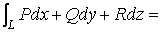
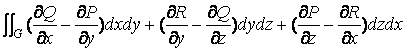( 17 )

переходит в формулу Грина, если положить z = 0 . Тогда dz = 0 и G 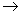D.

Из формулы Стокса легко получить условия при которых криволинейный интеграл по замкнутому контуру в пространстве обращается в ноль

; ;

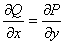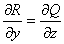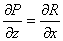
39. Поверхностный интеграл 2-го рода, Его свойства. Вычислительная форма

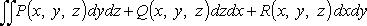
по фиксированной стороне двусторонней поверхности S.

Пови-2 по разным сторонам S⁺ и S ^- одной и той же поверхности S

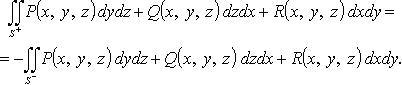
Сведение Пови-2 к двойному интегралу

1. Поверхность S задана параметрически: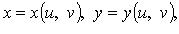

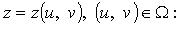
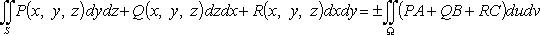
выбор знака перед интегралом согласуют со стороной поверхности, по которой ведется интегрирование.

2. Поверхность S задана уравнением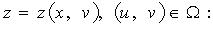

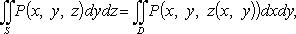
если Пови-2 вычисляется по верхней стороне поверхности S;

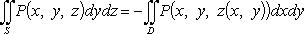
для нижней стороны поверхности S.

Свойства

1. Линейность: ;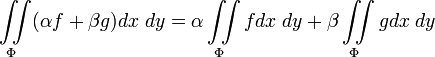

2. Аддитивность: ;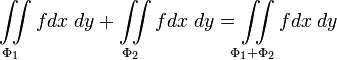

3. При изменении ориентации поверхности, поверхностный интеграл меняет знак.

38. Формула Гаусса-Остроградского и её приложения к вычислению поверхностных интегралов и объемов пространственной области.

Тройной интеграл после вычисления первого внутреннего интеграла превращается в двойной интеграл, который можно выразить через поверхностный.

Имеем тело ограниченное гладкими поверхностями : G1 – низ ,

z = z0(x,y) ; G2 – верх, z = Z(x,y) ; G3 - цилиндрическая боковая поверхность по границе области D на плоскости хОу. В этом объеме V определена функция R(x,y,z) , причем, функция и ее производные непрерывны. Рассмотрим интеграл

J= 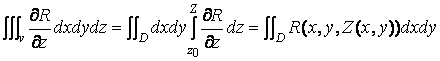- - 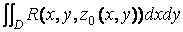= J1 – J2

По формуле ( 13 ) интеграл J1 сводится к интегралу по внешней поверхности «верха» тела, а J2 по внутренней поверхности «низа». При переходе на внешнюю сторону «низа» знак J2 меняется. Учтем также, что аналогичный интеграл J3 по боковой поверхности G3 равен нулю, т.к. площадь ее проекции на плоскость хОу равна нулю. В итоге имеем

J = + +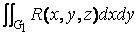

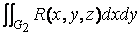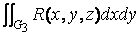
где интегралы вычисляются по внешней стороне поверхности ограничивающей тело, или

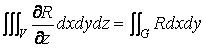( 18 )

Обобщение формулы ( 18 ) на случай тела произвольной формы приводит к формуле Остроградского – Гаусса

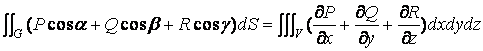( 19 )

которая интеграл по объему заменяет на интеграл по внешней стороне поверхности ограничивающей тело.

Вычисление объема.

Пусть подынтегральная функция в ( 4 ) не зависит от z , тогда она определяет некоторую поверхность z = f(x,y) , а интеграл по D объем цилиндрического бруса, ограниченного этой поверхностью и областью D . Переход к поверхностному интегралу в этом случае дает следующее выражение для объема цилиндрического бруса V = 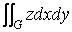( 14 ) Понятие о комплексных числах. Определение. Комплексным числом z называется выражение 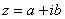, где a и b – действительные числа, i – мнимая единица, которая определяется соотношением: При этом число a называется действительной частью числа z (a = Re z), а b- мнимой частью (b = Im z).

Обобщение этой формулы на случай тела произвольной формы ограниченного поверхностью G имеет вид V = 1/3 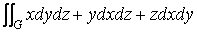( 15 )

36. Поверхностный интеграл 1-го рода, Его свойства. Вычислительная форма

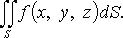
Сведение к двойному

1. Поверхность S задана уравнением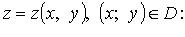

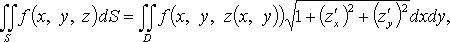
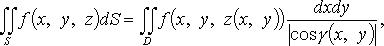
где 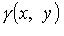- величина угла между нормалью к поверхности и положительным направлением оси Oz.

2. Поверхность S задана параметрически: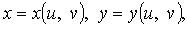

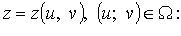
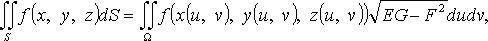
где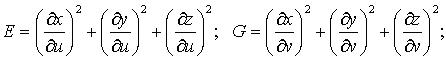

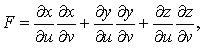или

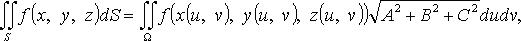
где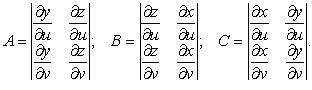

Свойства

1. Линейность: ;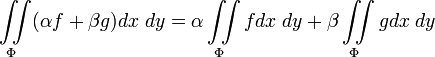

2. Аддитивность: ;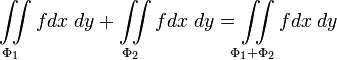

3. При изменении ориентации поверхности, поверхностный интеграл меняет знак.

33. Явные представления поверхности

32. Касательная плоскость и нормаль к поверхности

Пусть поверхность 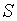задана уравнением 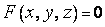(1)

в неявном виде. Будем считать, что 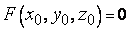и в некоторой окрестности точки 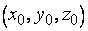функция 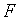имеет непрерывные частные производные, одновременно не равные нулю. Тогда

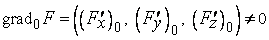(2)

Мы пишем 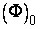вместо .

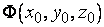Для определенности предположим, что 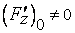. Тогда на основании теоремы о неявной функции существует окрестность точки 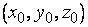, в которой поверхность 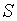описывается явно непрерывно дифференцируемой функцией 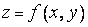. Уравнение касательной плоскости к 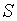в точке 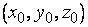, как мы знаем, имеет вид

,

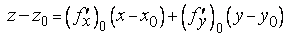где

.

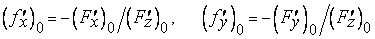В силу этого уравнения касательной плоскости к 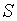в точке 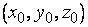запишется так:

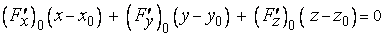, (3)

а уравнение нормали к 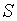в точке 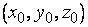- так:

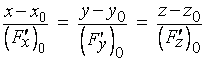. (4)

Те же уравнения (3), (4) мы получим, если предположить, что 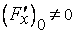или 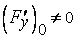. В этих случаях в окрестности 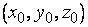поверхность 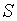описывается явно соответственно уравнениями

.

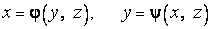Мы видим, что при условии (2) поверхность 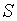в любой точке 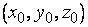имеет касательную плоскость, непрерывно изменяющуюся при непрерывном передвижении точки 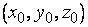. Такую поверхность называют гладкой поверхностью .

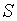Другое дело, если 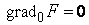. В этом случае нельзя гарантировать, что в точке 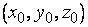существует касательная плоскость к 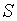. Она может существовать, а может и не существовать.

31. Ориентация гладкой поверхности

Гладкая поверхность ориентируема, если можно построить на ней непрерывное поле единичных нормальных векторов. Это поле единичных нормалей определяет ориентацию (или сторону) поверхности. На простой гладкой поверхности всегда определено непрерывное поле единичных нормальных векторов:

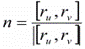
Произвольные гладкие поверхности могут быть как ориентируемыми (двусторонними), как и неориентируемыми (односторонними).Лист Мёбиуса.

26. Независимость криволинейного интеграла второго рода от пути интегрирования. Признак Грина

Пусть D - некоторая замкнутая область на плоскости хОу, ограниченная контуром L. На ней заданы функции Р = Р(х,у) и Q = Q(x,y), непрерывные на D вместе со своими частными производными первого порядка. Формула Грина связывает криволинейный интеграл второго рода по L с двойным интегралом по области D:

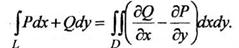
Движение по контуру L - в положительном направлении.

С помощью формулы Грина значение криволинейного интеграла по замкнутому контуру можно найти, вычислив двойной интеграл.

20. Формула Грина для многосвязной области

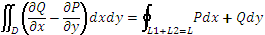
Формулу Грина можно применять, если область D – замкнутая, ограниченная кусочно-гладким контуром L, функции P(x,y) и Q(x,y) непрерывны и имеют частные производные первого порядка: 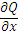и .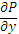

19. Формула Грина для односвязной области

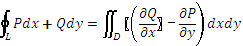
Формулу Грина можно применять, если область D – замкнутая, ограниченная кусочно-гладким контуром L, функции P(x,y) и Q(x,y) непрерывны и имеют частные производные первого порядка: 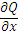и .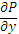

15. Криволинейный интеграл 1-го рода и его свойства. Вычислительная формула

Определение: Если при ∆l→0, σ имеет конечный предел, не зависящий ни от способа разбиений, ни от выбора точек Mk, то этот предел называется криволинейным интегралом первого рода от функции f(M) по кривой AB (интегрируется по длине дуги кривой) и обозначается 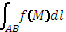или 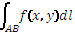. Таким образом .

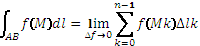Свойства: 1) Криволинейный интеграл первого рода не зависит от направления интегрирования; 2) Линейность; 3) Аддитивность; 4) Если f(M)≥0, то 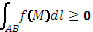; 5) f(M) интегрируема на АВ, следовательно |f(M)| тоже интегрируем на кривой АВ; 6) Среднее значение: 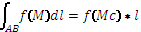, где l – длина кривой.

Способы вычисления криволинейного интеграла: 1) Кривая АВ: 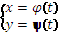, t0≤t≤t1, A→t=t0, B→t=t0, 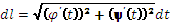, 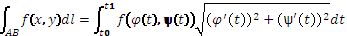; 2)АВ: y=y(x), a≤x≤b, A→x=a, B→x=b, ,

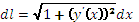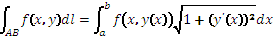
14. Физические приложении тройного интеграла