Движение заряженных частиц в электрическом поле.

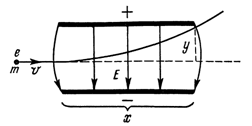
Пусть частица массой m и с зарядом e влетает со скоростью v в электрическое поле плоского конденсатора. Длина конденсатора x, напряженность поля равна Е. Смещаясь в электрическом поле вверх, электрон пролетит через конденсатор по криволинейной траектории и вылетит из него, отклонившись от первоначального направления на y. Под действием силы поля, F = eE = ma частица движется ускоренно по вертикали, поэтому 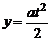. Время движения частицы вдоль оси ох с постоянной скоростью 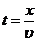. Тогда 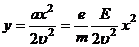. А это есть уравнение параболы. Т.о. заряженная частица движется в электрическом поле по параболе.

3. Движение заряженных частиц в магнитном поле.

Рассмотрим движение заряженной частицы в магнитном поле напряженностью Н. Силовые линии поля изображены точками и направлены перпендикулярно к плоскости рисунка (к нам).

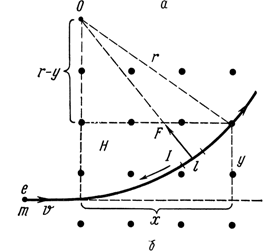
Движущаяся заряженная частица представляет собой электрический ток. Поэтому магнитное поле отклоняет частицу вверх от ее первоначального направления движения (направление движения электрона противоположно направлению тока)

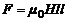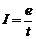Согласно формуле Ампера сила, отклоняющая частицу на любом участке траектории равна , ток , где t - время, за которое заряд e проходит по участку l. Поэтому 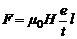. Учитывая, что 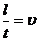, получим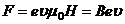

Сила F называется лоренцевой силой. Направления F, v и H взаимно перпендикулярны. Направление F можно определить по правилу левой руки.

Будучи перпендикулярна скорости 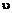, лоренцева сила изменяет только направление скорости движения частицы, не изменяя величины этой скорости. Отсюда следует, что:

1. Работа силы Лоренца равна нулю, т.е. постоянное магнитное поле не совершает работы над движущейся в нем заряженной частицей (не изменяет кинетической энергии частицы).

Напомним, что в отличие от магнитного поля электрическое поле изменяет энергию и величину скорости движущейся частицы.

2. Траектория частицы является окружностью, на которой частицу удерживает лоренцева сила, играющая роль центростремительной силы.

Радиус r этой окружности определим, приравнивая между собой лоренцеву и центростремительную силы:

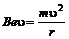, откуда .

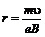Т.о. радиус окружности, по которой движется частица, пропорционален скорости частицы и обратно пропорционален напряженности магнитного поля.

Период обращения частицы T равен отношению длины окружности S к скорости частицы v: 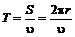. Учитывая выражение для r, получим 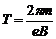. Следовательно, период обращения частицы в магнитном поле не зависит от ее скорости.

Если в пространстве, где движется заряженная частица, создать магнитное поле, направленное под углом 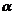к ее скорости 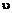, то дальнейшее движение частицы представит собой геометрическую сумму двух одновременных движений: вращения по окружности со скоростью 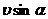в плоскости, перпендикулярной силовым линиям, и перемещения вдоль поля со скоростью 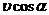. Очевидно, что результирующая траектория частицы окажется винтовой линией.

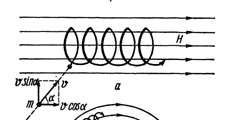
4. Электромагнитные счетчики скорости крови.

Принцип действия электромагнитного счетчика основан на движении электрических зарядов в магнитном поле. В крови имеется значительное количество электрических зарядов в виде ионов.

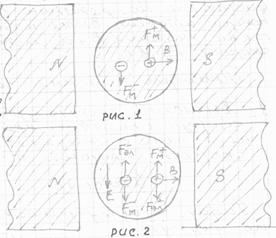
Предположим, что некоторое количество однозарядных ионов движется внутри артерии со скоростью . Если артерию поместить между полюсами магнита, ионы будут двигаться в магнитном поле.

Для направлений и B, показанных на рис.1., магнитная сила 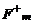, действующая на положительно заряженные ионы направлена вверх, а сила 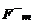, действующая на отрицательно заряженные ионы, направлена вниз. Под влиянием этих сил ионы движутся к противоположным стенкам артерии. Эта поляризация артериальных ионов создает поле E (рис.2), эквивалентное однородному полю плоского конденсатора. Тогда разность потенциалов в артерии U диаметром d связан с Е формулой 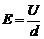. 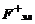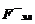Это электрическое поле, действуя на ионы, создает электрические силы и , направление которых противоположно направлению 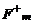и 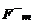, как показано на рис.2.

Концентрация зарядов на противоположных стенках артерии будет продолжаться до тех пор, пока электрическое поле не возрастет настолько, что = .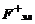

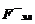Для состояния равновесия можно записать 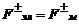; 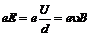, откуда .

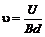Таким образом, скорость крови пропорциональна напряжению, возрастающему поперек артерии. Зная напряжение, а также значения B и d, можно определить скорость крови.

Примеры решения задач

1. Вычислить радиус дуги окружности, которую описывает протон в магнитном поле с индукцией 15 мТ, если скорость протона 2 Мм/с.

Решение:

Радиус дуги окружности определится по формуле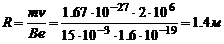

2. Протон, прошедший ускоряющую разность потенциалов U=600 В, влетел в однородное магнитное поле с индукцией В = 0,3Т и стал двигаться по окружности. Вычислить радиус R окружности.

Решение:

Работа, совершаемая электрическим полем при прохождении протона ускоряющей разности потенциалов, превращается в кинетическую энергию протона:

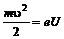(1)

Радиус окружности можно найти по формуле

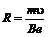(2)

Найдем из (1) v: 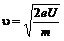Подставим это в (2):

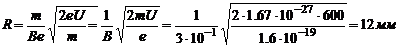
3. Какую энергию приобретет электрон, сделав 40 оборотов в магнитном поле циклотрона, используемого в целях радиационной терапии, если максимальное значение переменной разности потенциалов между дуантами U = 60кВ? Какую скорость приобретет протон?

Решение

За 1 оборот протон дважды пройдет между дуантами циклотрона и приобретет энергию 2eU. За N оборотов энергия T = 2eUN = 4,8 МэВ.

Скорость протона можно определить из соотношения 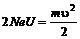, откуда

Лекция №7

1. Электромагнитная индукция. Закон Фарадея. Правило Ленца.

2. Взаимная индукция и самоиндукция. Энергия магнитного поля.

3. Переменный ток. Работа и мощность переменного тока.

4. Емкостное и индуктивное сопротивление.

5. Использование переменного тока в медицинской практике, его воздействие на организм.

1. Электромагнитная индукция. Закон Фарадея. Правило Ленца.

Ток, возбуждаемый магнитным полем в замкнутом контуре, называется индукционным током, а само явление возбуждения тока посредством магнитного поля – электромагнитной индукцией.

Электродвижущая сила, обуславливающая индукционный ток, называется электродвижущей силой индукции.

В замкнутом контуре индуцируется ток во всех случаях, когда происходит изменение потока магнитной индукции через площадь, ограниченную контуром – это закон Фарадея.

Величина ЭДС индукции 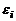пропорциональна скорости изменения потока магнитной индукции:

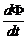~ (1)

Направление индукционного тока определяется правилом Ленца:

Индукционный ток имеет такое направление, что его собственное магнитное поле компенсирует изменение потока магнитной индукции, вызывающей этот ток:

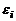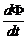=- (2)

[ ]

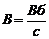2.Взаимная индукция и самоиндукция являются частным случаем электромагнитной индукции.

Взаимной индукцией называется возбуждение тока в контуре при изменении тока в другом контуре.

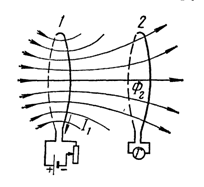
Предположим, что в контуре 1 идет ток I₁. Магнитный поток Ф₂, связанный с контуром 2, пропорционален магнитному потоку, связанному с контуром 1.

В свою очередь магнитный поток, связанный с контуром 1, ~ I_1, поэтому

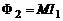, (3)

где M - коэффициент взаимной индукции. Предположим, что за время dt ток в контуре 1 изменяется на величину dI₁. Тогда, согласно формуле (3), магнитный поток, связанный с контуром (2), изменится на величину 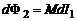, в результате чего в этом контуре появится ЭДС взаимной индукции (по закону Фарадея)

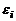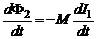= - . (4)

Формула (4) показывает, что электродвижущая сила взаимной индукции, возникающая в контуре, пропорциональна скорости изменения тока в соседнем контуре и зависит от взаимной индуктивности этих контуров.

Из формулы (3) следует, что

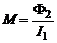(5)

Т.е. взаимная индуктивность двух контуров равна магнитному потоку, связанному с одним из контуров, когда в другом контуре идет ток, равный единице. M измеряется в Генри [Г = Вб/А].

Взаимная индуктивность зависит от формы, размеров и взаимного расположения контуров и от магнитной проницаемости среды, но не зависит от силы тока в контуре.

Контур, в котором изменяется ток, индуцирует ток не только в других, соседних, контурах, но и в себе самом: это явление называется самоиндукцией.

Магнитный поток Ф, связанный с контуром, пропорционален току I в контуре, поэтому

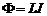, (6)

где L - коэффициент самоиндукции, или индуктивность контура.

Предположим, что за время dt ток в контуре изменяется на величину dI. Тогда из (6) 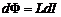, в результате чего в этом контуре появится ЭДС самоиндукции:

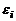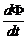
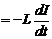=- . (7)

Из (6) следует, что 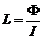. Т.е. индуктивность контура равна связанному с ним магнитному потоку, если в контуре идет ток, равный единице.

Явление электромагнитной индукции основано на взаимных превращениях энергий электрического тока и магнитного поля.

Пусть в некотором контуре с индуктивностью L включается ток. Возрастая от 0 до I, он создает магнитный поток .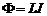

Изменение на малую величину dI сопровождается изменением магнитного потока на малую величину

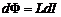(8)

При этом ток совершает работу dA = IdФ, т.е. 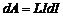. Тогда

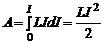. (9)

1. Переменный ток. Работа и мощность переменного тока.

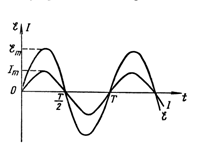
Синусоидальная ЭДС возникает в рамке, которая вращается с угловой скоростью в однородном магнитном поле индукцией В.

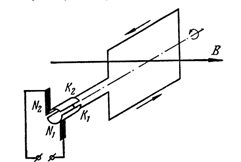
Поскольку магнитный поток

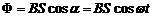, (10)

где 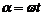- угол между нормалью к рамке n и вектором магнитной индукции В, прямо пропорционален времени t.

По закону электромагнитной индукции Фарадея

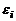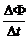=- , (11)

где 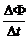- скорость изменения потока электромагнитной индукции. Тогда

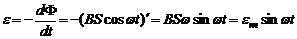, (12)

где 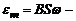амплитудное значение ЭДС индукции.

Эта ЭДС создает в контуре синусоидальный переменный ток силой:

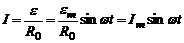, (13)

где 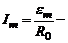максимальное значение силы тока, R₀ - омическое сопротивление контура.

Изменение ЭДС и силы тока совершаются в одинаковых фазах.

Эффективная сила переменного тока равна силе такого постоянного тока, который имеет ту же мощность, что и данный переменный ток:

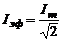(14)

Аналогично рассчитывается эффективное (действующее) значение напряжения:

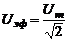(15)

Работа и мощность переменного тока рассчитываются с помощью следующих выражений:

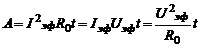(16)

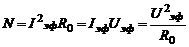(17)

4. Емкостное и индуктивное сопротивление.

Емкостное сопротивление. В цепи постоянного тока конденсатор представляет собой бесконечно большое сопротивление: постоянный ток не проходит через диэлектрик, разделяющий обкладки конденсатора. Цепи переменного тока конденсатор не разрывает: попеременно заряжаясь и разряжаясь, он обеспечивает движение электрических зарядов, т.е. поддерживает переменный ток во внешней цепи. Т.о., для переменного тока конденсатор представляет собой конечное сопротивление, называемое емкостным сопротивлением. Его величина определяется выражением:

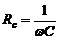, (18)

где 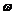- круговая частота переменного тока, С - емкость конденсатора

Индуктивное сопротивление. Из опыта известно, что сила переменного тока в проводнике, свернутом в виде катушки, значительно меньше, чем в прямом проводнике той же длины. Это означает, что помимо омического сопротивления проводник имеет еще дополнительное сопротивление, зависящее от индуктивности проводника и потому называемое индуктивным сопротивлением. Физический смысл его состоит в возникновении в катушке ЭДС самоиндукции, препятствующей изменениям тока в проводнике, а, следовательно, уменьшающей эффективный ток. Это равносильно появлению дополнительного (индуктивного) сопротивления. Его величина определяется выражением:

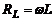, (19)

где L - индуктивность катушки. Емкостное и индуктивное сопротивления называются реактивными сопротивлениями. На реактивном сопротивлении электроэнергия не расходуется, этим оно существенно отличается от активного сопротивления. Организм человека обладает только емкостными свойствами.

Полное сопротивление цепи, содержащей активное, индуктивное и емкостное сопротивления, равно: .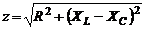

5. Использование переменного тока в медицинской практике, его воздействие на организм.

Действие переменного тока на организм существенно зависит от его частоты. При низких, звуковых и ультразвуковых частотах переменный ток, как и постоянный, вызывает раздражающее действие на биологические ткани. Это обусловлено смещением ионов растворов электролитов, их разделением, изменением их концентрации в разных частях клетки и межклеточного пространства. Раздражение тканей зависит также и от формы импульсного тока, длительности импульса и его амплитуды.

Так как специфическое физиологическое действие электрического тока зависит от формы импульсов, то в медицине для стимуляции нервной системы (электросон, электронаркоз), нервно-мышечной системы (кардиостимуляторы, дефибрилляторы) и т.д. используют токи с различной временной зависимостью.

Воздействуя на сердце, ток может вызвать фибрилляцию желудочков, которая приводит к гибели человека. Пропускание тока высокой частоты через ткань используют в физиотерапевтических процедурах, называемых диатермией и местной дарсонвализацией.

Токи высокой частоты используются также и для хирургических целей (электрохирургия). Они позволяют прижигать, «сваривать», ткани (диатермокоагуляция) или рассекать их (диатермотомия).

Примеры решения задач

1. В однородном магнитном поле индукцией В = 0,1 Т равномерно вращается рамка, содержащая N=1000 витков. Площадь рамки S=150см². Рамка вращается с частотой 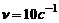. Определить мгновенное значение ЭДС, соответствующее углу поворота рамки в 30º.

Решение:

Мгновенное значение ЭДС индукции 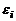определяется основным уравнением электромагнитной индукции:

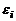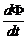=-N (1)

При вращении рамки магнитный поток, пронизывающий рамку, изменяется по закону:

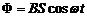(2)

Подставляя (2) в (1), получим: 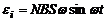. Поскольку 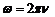, то =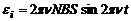

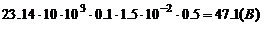
2. Если сила тока, проходящего в соленоиде, изменяется на 50 А в секунду, то на концах соленоида возникает среднее значение ЭДС самоиндукции, равное 0,08 В. Найти индуктивность соленоида.

Решение:

Индуктивность численно равна ЭДС самоиндукции, возникающей на концах соленоида, когда ток, проходящий через соленоид, равномерно изменяется на единицу силы тока в единицу времен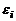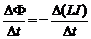и: =- или 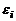= 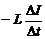. Знак (-) можно опустить, т.к. он показывает направление ЭДС

3. На стержень из немагнитного материала длиной l = 50 см и сечением S = 2см² намотан в один слой провод так, что на каждый сантиметр длины стержня приходится 20 витков. Определить энергию W магнитного поля внутри соленоида, если сила тока в обмотке I = 0,5А.

Решение:

Энергия магнитного поля соленоида с индуктивностью L, по обмотке которого течет ток I, выражается формулой

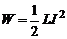(1)

Индуктивность соленоида в случае немагнитного сердечника зависит только от числа витков на единицу длины и от объема сердечника V:

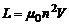, (2)

где 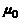постоянная.

Подставив в (1) выражение для L из (2), получаем:

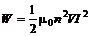(3)

Подставляя в (3) объем сердечника как V = Sl, получим:

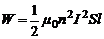(4)

Подставим в (4) численные значения:

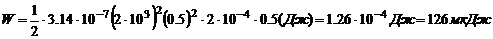
Лекция №8