Термодинамические процессы, циклы
Примеры решения задач
20.Азот массой 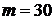 г занимает объем
г занимает объем 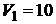 л и находиться под давлением
л и находиться под давлением 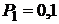 0 МПа. Сначала этот газ нагревается при неизменном давлении до объема
0 МПа. Сначала этот газ нагревается при неизменном давлении до объема 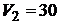 л, а затем при постоянном объеме до давления
л, а затем при постоянном объеме до давления 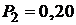 МПа. Найти:
МПа. Найти:
а) изменение 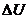 внутренней энергии газа;
внутренней энергии газа;
б) совершенную системой работу 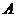 ;
;
в) количество теплоты 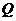 , переданной газу;
, переданной газу;
г) конечную температуру 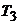 .
.
Построить график процесса на P – V-диаграмме.
Дано: 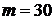 г г 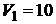 л л 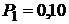 МПа МПа 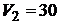 л л 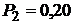 МПа МПа 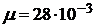 кг/моль кг/моль | Решение Анализ условия задачи начнём с построения графика процесса на P – V-диаграмме, учитывая соотношения величин 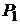 , , 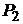 , , 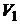 , , 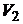 . . 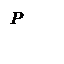  | |
а) 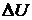 – ? б) – ? б) 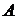 – ? в) – ? в) 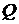 – ? г) – ? г) 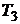 – ? – ? | ||
Как видно из рисунка, система из состояния 1 переходит в конечное состояние 3 сначала по изобаре 1 – 2, а затем по изохоре 2 – 3. Из графика следует, что работа 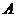 , совершенная газом в этом процессе, равна площади прямоугольника под изобарой 1 – 2, т. е.
, совершенная газом в этом процессе, равна площади прямоугольника под изобарой 1 – 2, т. е.
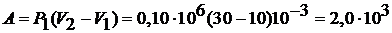 Дж.
Дж.
Для определения изменения внутренней энергии газа в рассматриеваемом процессе 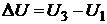 используем уравнение Клапейрона – Менделеева
используем уравнение Клапейрона – Менделеева
pV = 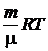 (1)
(1)
и выражение для внутренней энергии двухатомного идеального газа:
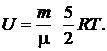 (2)
(2)
Из уравнений (1) и (2) для 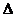 U следует
U следует
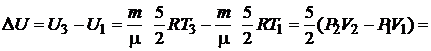
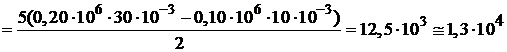 Дж.
Дж.
Из первого закона термодинамики для количества теплоты 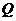 , переданного газу, получается:
, переданного газу, получается:
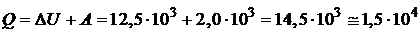 Дж.
Дж.
Из уравнения Клапейрона – Менделеева (1) для конечной температуры газа Т3 имеем:
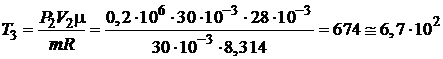 К.
К.
Ответ: 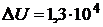 Дж;
Дж; 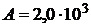 Дж;
Дж; 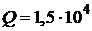 Дж;
Дж; 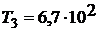 К.
К.
21.Одноатомный газ, имевший при давлении 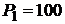 кПа объем
кПа объем 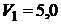 м3, сжимался изобарически до объема
м3, сжимался изобарически до объема 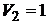 ,0 м3 , затем – адиабатически сжимался и на последнем участке цикла, расширялся при постоянной температуре до начального объема и давления. Найти теплоту
,0 м3 , затем – адиабатически сжимался и на последнем участке цикла, расширялся при постоянной температуре до начального объема и давления. Найти теплоту 
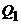 , полученную газом от нагревателя, теплоту
, полученную газом от нагревателя, теплоту 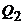 , переданную газом холодильнику, работу
, переданную газом холодильнику, работу 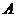 , совершенную газом за весь цикл, КПД цикла
, совершенную газом за весь цикл, КПД цикла 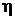 . Изобразить цикл на P – V-диаграмме.
. Изобразить цикл на P – V-диаграмме.
Дано: 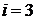 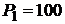 кПа кПа 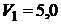 м3 м3 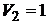 ,0 м3 ,0 м3 | Решение Анализ условия задачи начнём с построения графика цикла на P – V-диаграмме, учитывая соотношения величин  , ,  , , 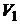 , , 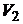 , , 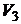 . .   | |
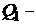 ? ? 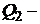 ? ? 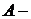 ? ? 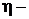 ? ? | ||
Как видно из рисунка, на первом участке цикла 1 – 2 газ сжимался изобарически, отдавая холодильнику количество теплоты 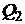 и совершая работу
и совершая работу 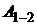 . По первому закону термодинамики для перехода из состояния 1 в состояние 2 можно записать:
. По первому закону термодинамики для перехода из состояния 1 в состояние 2 можно записать:
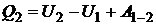 , (1)
, (1)
где 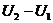 – изменения внутренней энергии газа. Выражение для внутренней энергии одноатомного газа имеет вид:
– изменения внутренней энергии газа. Выражение для внутренней энергии одноатомного газа имеет вид:
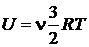 , (2)
, (2)
где 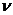 – количество вещества, а уравнение Клапейрона – Менделеева:
– количество вещества, а уравнение Клапейрона – Менделеева:
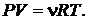 (3)
(3)
Используем уравнения (2), (3) и тот факт, что работа газа на участке 1 – 2 равна площади прямоугольника (с обратным знаком) под изобарой 1 – 2, для количества теплоты 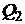 из соотношения (1) получим
из соотношения (1) получим
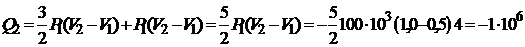 Дж.
Дж.
Знак “минус” показывает, что количество теплоты 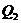 отдаётся газом холодильнику.
отдаётся газом холодильнику.
Количество теплоты 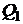 , которое получает газ от нагревателя на изотерме 3 – 1 при температуре
, которое получает газ от нагревателя на изотерме 3 – 1 при температуре 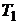 , по первому закону термодинамики равно:
, по первому закону термодинамики равно:
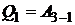 , (4)
, (4)
где 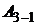 – работа, совершённая газом на участке 3 – 1.
– работа, совершённая газом на участке 3 – 1.
Как известно, работа газа при изотермическом процессе определяется формулой
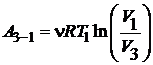 . (5)
. (5)
Состояния (3) и (1) находятся на одной изотерме, поэтому
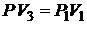 . (6)
. (6)
В то же время состояния (3) и (2), как видно из рисунка, соответствует одной адиабате, поэтому из уравнения Пуассона следует
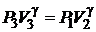 (7)
(7)
где 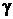 – показатель адиабаты одноатомного идеального газа
– показатель адиабаты одноатомного идеального газа 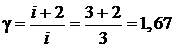 . Исключая из уравнений (6) и (7) величины давления
. Исключая из уравнений (6) и (7) величины давления  и
и  , получим
, получим 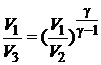 (8)
(8)
Используя формулы (3), (5) и (8) для количества теплоты 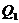 из соотношения (4) имеем
из соотношения (4) имеем
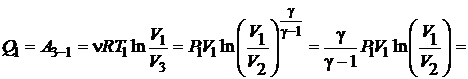
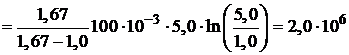 Дж.
Дж.
Работа 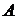 , совершённая газом за цикл, как вытекает из первого закона термодинамики,
, совершённая газом за цикл, как вытекает из первого закона термодинамики, 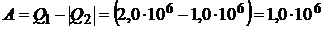 Дж.
Дж.
Для КПД цикла 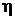 имеем:
имеем: 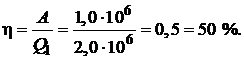
Ответ: 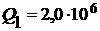 Дж;
Дж; 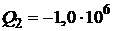 Дж;
Дж; 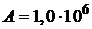 Дж;
Дж; 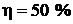
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
2.20. Молекулярный кислород массой m = 250 г, имевший температуру Т1 = 200 К, был адиабатно сжат. При этом была совершена работа А = 25 кДж. Определить конечную температуру Т2 газа.
(354 K)
2.21. Газ адиабатически расширяется, изменяя объем в 2 раза, а давление в 2,64 раза. Определить молярные теплоемкости Cp и Cv этого газа.
(Cp = 29,1 Дж/(моль×К), Cv = 20,8 Дж/(моль×К))
2.22. Некоторое количество азота n, имеющего параметры состояния p1, V1, T1, переходит при постоянной температуре в состояние 2, а затем при постоянном объеме – в состояние 3. Определить работу перехода 1 – 3, изменение внутренней энергии газа и теплоту, полученную при переходах, если в конце процесса установилась температура T3 и давление p3 = p1. Изобразить процесс 1 – 3 на диаграмме V-T.
(A1-3 = nRT1ln(T3/T1); DU1-3 = (5/2)nR(T3 – T1);
Q = nR[(5/2)(T3-T1)+T1ln(T3/T1)])
2.23. Азот плотностью r1 = 1,4 кг/м3 занимает объем V1 = 5 л при температуре t1 = 27 °C. Газ адиабатически переведен в состояние с плотностью r = 3,5 кг/м3. Определить температуру газа T2 в конце перехода и изменение его внутренней энергии. Построить переход на диаграмме S – T.
(T2 = 433 К; DU = 691 Дж)
2.24. Нагревается или охлаждается идеальный газ, если он расширяется по закону р1/2×V = const? Изобразите этот закон на диаграмме (V – T). Считая этот процесс политропическим, определить, чему равен показатель политропы h. При расширении газа тепло подводится к нему или отводится от него? Сравнить теплоёмкость С этого процесса с СV.
(СV > С)
2.25. Нагревается или охлаждается идеальный газ, если он расширяется по закону р2V = const? Изобразите этот закон на диаграмме (р-Т). Считая этот процесс политропическим, определить чему равен показатель политропы h. При расширении газа тепло подводится к нему или отводится от него? Сравнить теплоёмкость С этого процесса с СV.
η = 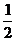 ; С>Сv)
; С>Сv)
2.26. В сосуде вместимостью V = 10 л находится идеальный газ под давлением p1 = 1,0×105 Па. Стенки сосуда могут выдержать максимальное давление p2 = 1,0×106 Па. Какое максимальное количество тепла Q можно сообщить газу? Постоянная адиабаты g = 1,4.
(Q = 23 кДж)
2.27. Некоторую массу азота сжали в 5 раз (по объёму) двумя разными способами: один раз изотермически, другой раз адиабатически. Начальное состояние газа в обоих случаях одинаково. Найти отношение соответствующих работ, затраченных на сжатие газа. Изобразить процессы в координатах P – V и Т – S.
(AТ/AА = 0,712)
2.28. В бензиновом автомобильном двигателе степень сжатия горючей смеси равна 6,2. Смесь засасывается в цилиндр при температуре t1 = 15 °C. Найти температуру t2 горючей смеси к концу такта сжатия. Горючую смесь рассматривать как двухатомный идеальный газ, процесс считать адиабатным.
(324 °С)
2.29. Тепловая машина работает по циклу Карно, КПД которого h = 0,25. Каков будет холодильный коэффициент k 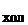 машины, если она будет совершать тот же цикл в обратном направлении? Холодильным коэффициентом называется отношение количества теплоты, отнятого от охлаждаемого тела, к работе двигателя, приводящего в движение машину.
машины, если она будет совершать тот же цикл в обратном направлении? Холодильным коэффициентом называется отношение количества теплоты, отнятого от охлаждаемого тела, к работе двигателя, приводящего в движение машину.
(k 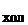 = 3)
= 3)
2.30. Один моль одноатомного идеального газа совершает тепловой цикл Карно между тепловыми резервуарами с температурами t1 = 127 °С и t2 = 27 °С. Наименьший объем газа в ходе цикла V1 = 5,0 л, наибольший V3 = 20 л. Какую работу А совершает эта машина за один цикл? Сколько тепла Q1 берет она от высокотемпературного резервуара за один цикл? Сколько тепла Q2 поступает за цикл в низкотемпературный резервуар?
(Q1 = 3,2×103 Дж; Q2 = 2,4×103 Дж; A = 8,1×102 Дж)
2.31.Трехатомный идеальный газ с жесткой связью между молекуламисовершает цикл Карно, при этом в процессе адиабатного расширения объем газа увеличивается в 4 раза. Определите термический КПД цикла.
( 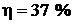 )
)
2.32. Найти КПД цикла, состоящего из двух изохор и двух изотерм, если в пределах цикла объём изменяется в k раз, а абсолютная температура в t раз. Рабочим веществом является идеальный газ с показателем адиабаты g.
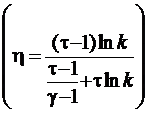
Энтропия
Пример решения задачи
22. При нагревании двухатомного идеального газа ( 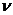 = 2 моля) его термодинамическая температура увеличилась в 2 раза (n = 2). Определите изменение энтропии, если нагревание происходит: 1)изохорно; 2) изобарно.
= 2 моля) его термодинамическая температура увеличилась в 2 раза (n = 2). Определите изменение энтропии, если нагревание происходит: 1)изохорно; 2) изобарно.
Дано: i = 5 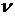 = 2,0 моля = 2,0 моля 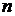 = = 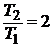 1) V = const 2) p = const 1) V = const 2) p = const | Решение 1)V = const. Из определения энтропии 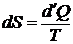 . Изменение энтропии . Изменение энтропии 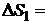 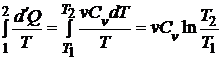 , где , где  – молярная теплоёмкость при постоянном давлении. Так как – молярная теплоёмкость при постоянном давлении. Так как 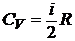 , то , то 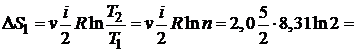 = 28,8 Дж/К = 28,8 Дж/К 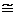 29 Дж/К 29 Дж/К |
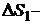 ? ? 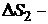 ? ? |
2) р = const.
Учитывая что 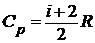 , где
, где 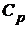 – молярная теплоёмкость при постоянном давлении аналогично п. 1 получим:
– молярная теплоёмкость при постоянном давлении аналогично п. 1 получим:
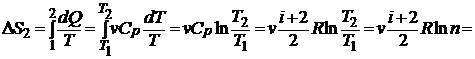
= 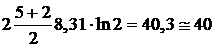 Дж/К.
Дж/К.
Ответ: 1) 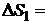 29 Дж/К; 2)
29 Дж/К; 2) 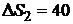 Дж/К.
Дж/К.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
2.33. Какое количество тепла Q нужно сообщить 75 г водяных паров, чтобы нагреть их от 100 С до 250 °С при постоянном давлении? Определите изменение энтропии водяного пара.
(Q = 20,8 кДж; DS = 47,5 Дж/К)
2.34. Определить изменение DS энтропии при изотермическом расширении кислорода массой m = 10 г от объема V1 = 25 л до объема V2 = 100 л. (Относительная молекулярная масса кислорода 32).
(3,6 Дж/К)
2.35. Найти изменение DS энтропии при нагревании воды массой m = 100 г от температуры t1 = 0 °C до температуры t2 = 100 °C и последующим превращении воды в пар той же температуры. Удельная теплоемкость воды C = 4,18 кДж/(кг×К), удельная теплота парообразования воды 2,25×103 кДж/кг.
(737Дж/К)
2.36. Найти изменение DS энтропии при превращении массы m = 200 г льда, находившегося при температуре t1 = -10,7 °C в воду при t2 = 0 °C.
Теплоемкость льда считать не зависящей от температуры. С = 2,1×103 Дж/(кг×К). Температуру плавления принять равной 273 К.Удельная теплота плавления льда l = 333×103 Дж/кг.
(DS = m[C×ln(T2/T1)+l/T2] = 261 Дж/К)
2.37. Один киломоль газа изобарически нагревается от 20 до 600 °С, при этом газ поглощает 1,20×107 Дж тепла. Найти число степеней свободы молекулы газа i; построить зависимость энтропии S как функцию от температуры Т газа.
(i = 3)
ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ
Электростатика. Диэлектрики
Примеры решения задач
23. По тонкому кольцу равномерно распределен заряд Q = 40 нКл с линейной плотностью 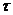 = 50 нКл/м. Определить напряженность
= 50 нКл/м. Определить напряженность 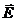 электрического поля, создаваемого этим зарядом в точке А, лежащей на оси кольца и удаленной от его центра на расстояние, равное половине радиуса.
электрического поля, создаваемого этим зарядом в точке А, лежащей на оси кольца и удаленной от его центра на расстояние, равное половине радиуса.
Дано: Q = 40 нКл = 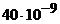 Кл Кл 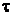 = 50 нКл/м = = = 50 нКл/м = = 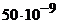 Кл/м h = Кл/м h = 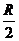 |
 |

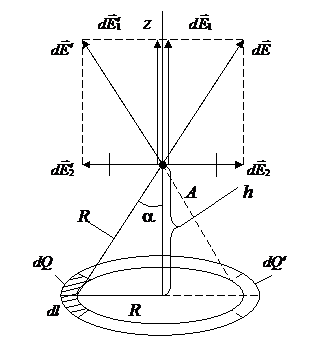
Напряженность поля, создаваемого этим зарядом 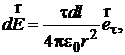
где 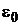 – электрическая постоянная;
– электрическая постоянная; 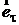 – единичный вектор, направленный вдоль r . Разложим вектор
– единичный вектор, направленный вдоль r . Разложим вектор 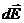 на две составляющие:
на две составляющие: 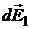 вдоль оси Z, и
вдоль оси Z, и 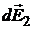 , перпендикулярную оси z ,т.е.
, перпендикулярную оси z ,т.е.
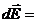
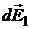
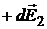 .
.
Напряжённость 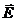 электрического поля в точке А найдём интегрированием
электрического поля в точке А найдём интегрированием
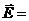
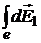
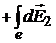 ,
,
где интегрирование ведется по всем элементам заряженного кольца. Заметим, что для каждой пары зарядов dQ и d 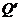 , расположенных симметрично относительно центра кольца, векторы
, расположенных симметрично относительно центра кольца, векторы 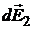 и
и 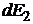 , в точке А равны по модулю и противоположны по направлению
, в точке А равны по модулю и противоположны по направлению 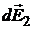 = –
= – 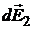 , т.е компенсируют друг друга.
, т.е компенсируют друг друга.
Составляющие 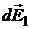 для всех элементов кольца сонаправлены с осью z, т.е.
для всех элементов кольца сонаправлены с осью z, т.е. 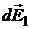 =
= 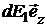 .
.
Тогда 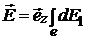
Так как 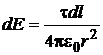 ,
, 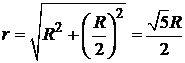 ;
; 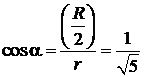 , то
, то
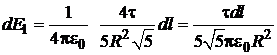 .
.
Таким образом 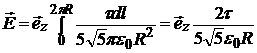 .
.
Поскольку 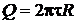 , то радиус кольца
, то радиус кольца 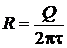 .
.
Тогда 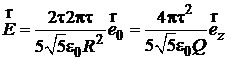 .
.
Значение напряженности на расстоянии z = h = R/2.
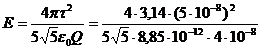 = 7000 В/м = 7,9 кВ/м
= 7000 В/м = 7,9 кВ/м
Ответ: Е = 7,9 кВ/м.
24. Электрическое поле создается бесконечным цилиндром радиусом R, равномерно заряженным с линейной плотность τ. Определите разность потенциалов между двумя точками этого поля, лежащими на расстоянии 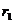 и
и 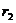 от поверхности этого цилиндра. Решение
от поверхности этого цилиндра. Решение
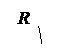 | |||
 | |||
        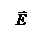 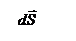      Дано Дано 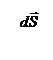   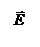 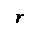      R R 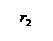  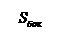  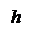  τ τ 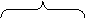    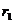  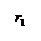  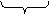    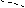 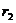 |
   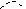 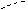  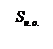 φ1 – φ2 ? φ1 – φ2 ? |
Интегрирал по гауссовой поверности, верхности раскладываем на три интеграла: по верхнему и нижнему основаниям, по боковой поверхности. Интеграл по верхнему основанию 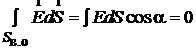 , так как угол
, так как угол 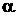 между вектором элементарной площадки
между вектором элементарной площадки 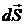 и вектором
и вектором 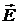 равен π /2 и cos π /2 = 0. Аналогично для нижнего основания. Остается интеграл по боковой поверхности
равен π /2 и cos π /2 = 0. Аналогично для нижнего основания. Остается интеграл по боковой поверхности 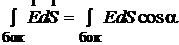 , здесь угол
, здесь угол 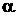 = 0, cos 0 = 1, значение напряженности Е на одном и том же расстоянии r одинаково, Е выносим за знак интеграла
= 0, cos 0 = 1, значение напряженности Е на одном и том же расстоянии r одинаково, Е выносим за знак интеграла 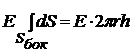 . В правой части теоремы Гаусса заряд, охватываемый гауссовой поверхностью
. В правой части теоремы Гаусса заряд, охватываемый гауссовой поверхностью 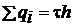 . Таким образом, получаем
. Таким образом, получаем
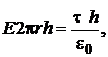
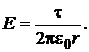
Для нахождения разности потенциалов воспользуемся связью напяженности и потенциала
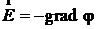 .
.
Для случая радиальной симметрии, реализующейся у нас,
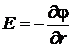 .
.
Интегрируя это выражение, получим
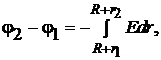 или
или
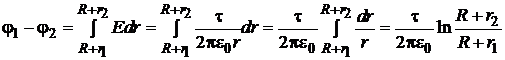 .
.
Ответ: 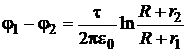 .
.
25. Плоский конденсатор, между обкладками которого помещена стеклянная пластинка  (
( 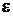 = 6) толщиной l = 2,00 мм, заряжен до напряжения U = 200 В (рис. 1). Пренебрегая величиной заряда между пластинкой и обкладками, найти а) поверхностную плотность
= 6) толщиной l = 2,00 мм, заряжен до напряжения U = 200 В (рис. 1). Пренебрегая величиной заряда между пластинкой и обкладками, найти а) поверхностную плотность 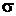 свободных зарядов на обкладках конденсатора, а также б) поверхностную плотность
свободных зарядов на обкладках конденсатора, а также б) поверхностную плотность 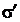 связанных зарядов (зарядов поляризации) на стекле. Изобразить силовые линии электрического поля в стекле и воздушном зазоре между стеклом и обкладками.
связанных зарядов (зарядов поляризации) на стекле. Изобразить силовые линии электрического поля в стекле и воздушном зазоре между стеклом и обкладками.
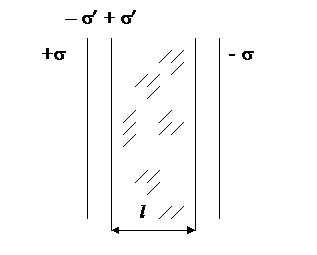 Дано: Дано:
U = 200 В | ||
σ – ? σ´ – ?  силовые линии Е силовые линии Е |
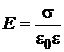 (1)
(1)
Отсюда, учитывая соотношение Е = 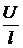 , справедливое для однородного поля конденсатора, найдем:
, справедливое для однородного поля конденсатора, найдем:
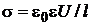 (2)
(2)
Чтобы определить величину 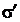 , воспользуемся формулой
, воспользуемся формулой 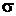 =
= 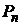 (поверхностная плотность связанных зарядов равна проекции вектора поляризованности
(поверхностная плотность связанных зарядов равна проекции вектора поляризованности 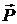 на внешнюю нормаль к поверхности диэлектрика). Так как вектор
на внешнюю нормаль к поверхности диэлектрика). Так как вектор 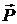 параллелен вектору напряженности
параллелен вектору напряженности 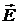 поля в диэлектрике, направленному по нормали к поверхности стеклянной пластинки, то
поля в диэлектрике, направленному по нормали к поверхности стеклянной пластинки, то 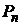 =
= 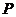 . Учитывая соотношение
. Учитывая соотношение 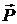 = æ
= æ 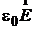 , где æ – диэлектрическая проницаемость среды и соотношение
, где æ – диэлектрическая проницаемость среды и соотношение 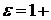 æ, получим:
æ, получим:
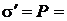 æ
æ 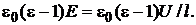 (3)
(3)
Подставляя в формулы (2) и (3) величины в единицах СИ: U = 200 B, 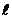 = 2,00
= 2,00 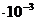 м,
м, 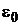 = 8.85
= 8.85 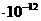 Ф/м, найдем:
Ф/м, найдем:
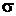 =
= 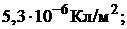
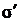 =
= 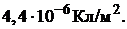
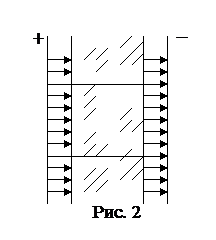 Чтобы изобразить силовые линии электрического поля в стекле и воздуш ном зазоре, надо помнить, что густота силовых линий пропорциональна напряженности поля, а диэлектрическая проницаемость среды
Чтобы изобразить силовые линии электрического поля в стекле и воздуш ном зазоре, надо помнить, что густота силовых линий пропорциональна напряженности поля, а диэлектрическая проницаемость среды 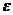 показывает во сколько раз поле внутри диэлектрика слабее поля внутри зазора, следовательно густота силовых линий внутри стеклянной пластинки в шесть раз меньше, чем в зазоре (рис. 2).
показывает во сколько раз поле внутри диэлектрика слабее поля внутри зазора, следовательно густота силовых линий внутри стеклянной пластинки в шесть раз меньше, чем в зазоре (рис. 2).
Ответ: 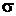 =
= 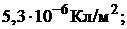
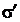 =
= 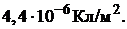
26. Определить дивергенцию следующих векторных полей:
a) 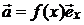 , где f(x) – некоторая функция декартовой координаты х;
, где f(x) – некоторая функция декартовой координаты х;
b) 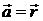 , где
, где 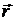 – радиус-вектор точки, в которой определяется дивергенция.
– радиус-вектор точки, в которой определяется дивергенция.
Дано: а) 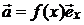 ; b) ; b) 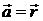 | Решение По определению 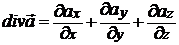 . a) . a) 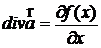 ; b) Выразим радиус-вектор через компоненты: ; b) Выразим радиус-вектор через компоненты: |
div 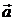 - ? - ? |
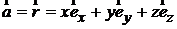 ,
,
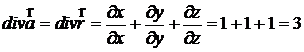 .
.
Ответ:а) 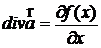 ; b) div
; b) div 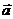 = 3.
= 3.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
3.1. Шар радиусом R заряжен однородно с объёмной плотностью r. Найти напряженность поля 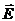 для точек внутри и вне шара.
для точек внутри и вне шара.
( 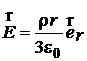 ;
; 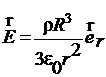 )
)
3.2. Бесконечно тонкая прямая нить заряжена однородно с плотностью l. Найти напряженность электрического поля Е и потенциал j как функции расстояния r от нити. Потенциал на расстоянии r0 положить равным нулю.
(E = (1/2pe0) l/r; j = -(l/2pe0) ln(r/r0))
3.3. Тонкий длинный стержень равномерно заряжен с линейной плотностью t = 1,5 нКл/см. На продолжении оси стержня на расстоянии d = 12 см от его конца находится точечный заряд Q = 0,20 мкКл. Определить силу взаимодействия заряженного стержня и точечного заряда.
(F = 2,2 мН)
3.4. По тонкому проволочному кольцу радиусом r = 60 мм равномерно распределен заряд q = 20 нКл.
а) приняв ось кольца за ось х, найти потенциал j и напряженность поля 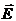 на оси кольца как функцию х (начало отсчета х поместить в центр кольца);
на оси кольца как функцию х (начало отсчета х поместить в центр кольца);
б) исследовать случаи х = 0 и ½х½>> r.
(E = (1/4pe0)× 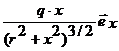 ; j = (1/4pe0)
; j = (1/4pe0) 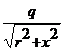 )
)
3.5. Чему равен поток вектора 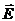 через поверхность сферы, внутри объема которой находится:
через поверхность сферы, внутри объема которой находится:
а) заряд е;
б) заряд -е;
в) диполь с моментом 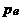 ?
?
Объясните результат с помощью картины силовых линий электрического поля.
3.6. Металлический шар радиусом R помещен в однородное электрическое поле. Изобразите качественную картину силовых и эквипотенциальных линий электрического поля.
3.7. Два точечных заряда +е и -е расположены в точках с координатами (а/2,0,0), (-а/2,0,0). Построить качественно график зависимости проекции напряженности поля Ех(х) для точек, лежащих на оси х (у = 0).
3.8. Найти зависимость плотности зарядов от декартовых координат ρ(x,y, z), при которой напряженность поля описывалась бы функцией 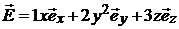 (В/м).
(В/м).
(ρ(x,y, z) = 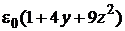 Кл/м3)
Кл/м3)
3.9. Потенциал поля, создаваемого некоторой системой зарядов, имеет вид: j = a(x2+y2)-bz2, где а и b – положительные константы. Найти напряженность поля Е и ее модуль ½Е½. Построить графики зависимости Ex = f(x), Ez = f(z).
(E = 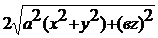 ;
; 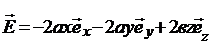 )
)
3.10. Плоский воздушный конденсатор подключили к батарее, а затем отключили от неё. После этого уменьшим расстояние между пластинами конденсатора в 2 раза. Как изменится:
а) энергия, запасенная конденсатором;
б) заряд на обкладках конденсатора;
в) плотность энергии электрического поля конденсатора?
3.11. Диэлектрическая пластина шириной 2а с проницаемостью e = 2 помещена в однородное электрическое поле напряженности Е, силовые линии которого перпендикулярны пластине.
а) изобразите на рисунке линии полей Е и D электрического поля;
б) постройте качественно графики зависимостей Ех, Dх от х (ось х перпендикулярна пластине, вектор Е направлен вдоль оси х, точка х = 0 находится в середине пластины).
3.12. Диэлектрическая пластинка с проницаемостью e = 2 помещена в однородное электрическое поле с напряженностью Е. Линии поля Е образуют некоторый угол j с поверхностью пластины. Изобразите качественно линии полей Е и D в вакууме и в пластине. Постройте качественно графики зависимостей Еx = f(x) и Dx = f(x).
3.13. Внутри плоской однородной диэлектрической пластины с e = 3 вектор напряженности однородного электрического поля составляет угол j с поверхностью пластины. Считая, что с одной стороны пластины вакуум, а с другой стороны диэлектрик с e = 2, изобразить качественно линии Е и D электрического поля в трех указанных средах. Построить качественно зависимости Еx = f(x) и Dx = f(x). Ось ОХ перпендикулярна поверхностям пластины, а ее толщина d.
3.14. Плоский воздушный конденсатор опустили в воду так, что поверхность воды параллельна плоскостям пластин, а ее уровень расположен на расстоянии h от нижней пластины. Найти зависимость электроемкости конденсатора от величины h, если площадь пластины S, а расстояние между ними d.
(С = 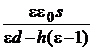 )
)
3.15. Электрическое поле создается равномерно заряженным шаром радиусом R с объемной плотностью заряда r. Определить зависимость вектора электрического смещения электрического поля от r. Построить качественно график D = f(r).
(D = (1/3)rr; D = (r/3)×(R3/r2))
Постоянный ток
Примеры решения задач
27. Пространство между пластинами плоского конденсатора заполнено многослойным диэлектриком, обладающим слабой электропроводностью. Диэлектрическая проницаемость диэлектрика 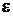 монотонно уменьшается от пластины 1 от значения
монотонно уменьшается от пластины 1 от значения 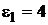 до значения
до значения 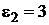 у пластины 2. Удельная электропроводность
у пластины 2. Удельная электропроводность 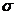 монотонно уменьшается от пластины 1 от значения
монотонно уменьшается от пластины 1 от значения 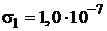 Ом.-1 м-1 до значения
Ом.-1 м-1 до значения 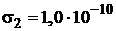 Ом.-1 м-1 у пластины 2. Конденсатор включен в цепь с постоянной ЭДС, и в нем устанавливается постоянный электрический ток силой
Ом.-1 м-1 у пластины 2. Конденсатор включен в цепь с постоянной ЭДС, и в нем устанавливается постоянный электрический ток силой 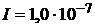 А, текущий через диэлектрик от стороны 1 конденсатора к стороне 2. Найти величину свободного заряда
А, текущий через диэлектрик от стороны 1 конденсатора к стороне 2. Найти величину свободного заряда 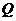 , возникшего в диэлектрике при протекании тока.
, возникшего в диэлектрике при протекании тока.
Дано: 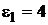 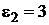 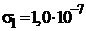 Ом.-1м-1 Ом.-1м-1 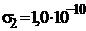 Ом.-1м-1 Ом.-1м-1 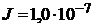 А А | Решение Среда между пластинами конденсатора обладает как электропроводящими, так и диэлектрическими свойствами. Поэтому в решении используется закон Ома в диф |

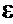 =
= 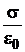 , с учетом наличиия диэлектрика
, с учетом наличиия диэлектрика 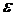 = 6,0
= 6,0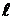 = 2,00 мм
= 2,00 мм