Момент количества движения точки.

В некоторых задачах в качестве динамической характеристики движущейся точки вместо самого количества движения рассматривают его момент относительно какого-либо центра или оси. Эти моменты определяются также как и моменты силы.

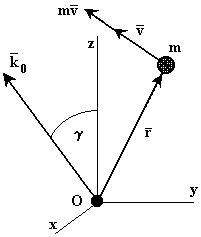Моментом количеством движения материальной точки 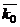относительно некоторого центра О называется вектор, определяемый равенством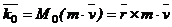

Момент количества движения точки называют также кинетическим моментом.

Момент количества движения относительно какой-либо оси 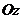, проходящий через центр О, равен проекции вектора количества движения 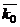на эту ось .

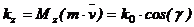Теорема об изменении момента количества движения точки.

Теорема. Производная по времени от момента количества движения точки, взятого относительно какого-нибудь центра, равна моменту действующей на точку силы относительно того же центра.

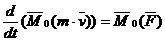
Теорема. Производная по времени от момента количества движения точки, взятого относительно какой-либо оси, равна моменту действующей на точку силы относительно той же оси.

Следствия из теорем:

1. Если момент силы относительно точки равен нулю, то момент количества движения относительно этой точки величина постоянная.

,

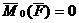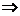
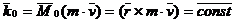
2. Если момент силы относительно оси равен нулю, то момент количества движения относительно этой оси величина постоянная.

,

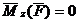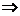
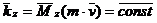
Кинетическая энергия точки

Кинетической энергией материальной точки (или ее живой силой) называют половину произведения массы точки на квадрат ее скорости.

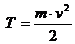
Теорема об изменении кинетической энергии точки.

Теорема. Дифференциал кинетической энергии точки равен элементарной работе силы, действующей на точку.

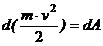
Теорема. Производная по времени от кинетической энергии точки равна мощности, подводимой к этой точке.

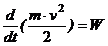
Теорема. Изменение кинетической энергии точки на каком-либо перемещении равно работе силы, действующей на точку на этом же перемещении.

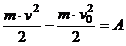
Классификация сил, действующих на систему мат. точек

Силы, действующие на любую точку механической системы, делятся на внутренние и внешние.

Fi – внутренняя сила

Fe – внешняя сила

Внутренними называются силы, с которыми точки, входящие в систему, действуют друг на друга.

Внешними называются силы, которые прикладываются к точкам извне, то есть от других точек или тел, не входящих в систему. Разделение сил на внутренние и внешние условное.

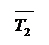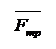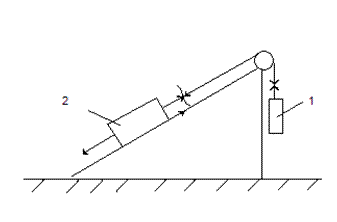mg – внешняя сила

Fтр – внутренняя сила

Дифференциальные уравнения системы в векторной форме:

,

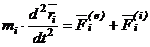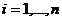
Центр масс системы

Центр масс системы – геометрическая точка, положение которой определяется радиус-вектором .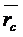

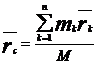, где

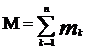
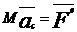(4)

- теорема о движении центра масс системы: центр масс системы движется также, как точка, масса которой равна массе всей системы под действием сил, приложенных к системе.

Для решения задач запишем теорему в проекциях на оси координат:

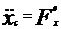M 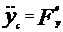; M ; M .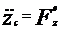

Теорема об изменении количества движения точки и системы : производная по времени от количества движения точки равна приложенной силе.

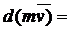
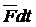(6)

Дифференциал от количества движения точки равен элементарному импульсу силы.

=

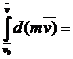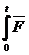
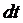
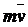
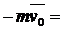
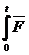
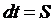(полный импульс силы) (7)

– теорема в интегральной форме: изменение количества движения точки за некоторый промежуток времени равен импульсу силы за этот промежуток времени.