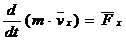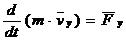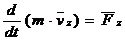Диф.уравнения движения материальной точки.

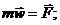
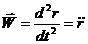
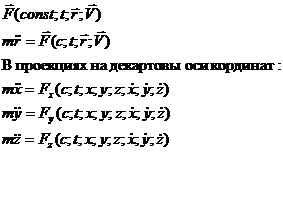
При плоском движении точки:

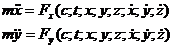
Если тело движется прямолинейно, то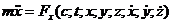

В проекциях на естественные оси координат:

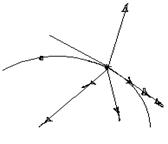
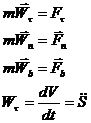
, где S- закон движения точки по траектории.

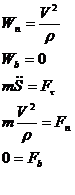
Принцип Даламбера для материальной точки

Уравнение движения материальной точки относительно инерциальной системы отсчета под действием приложенных активных сил и сил реакции связей имеет вид:

,

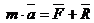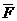- равнодействующая активных сил, 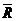- равнодействующая сил реакции связей.

Силой инерции материальной точки называют произведение массы точки на вектор ускорения, взятое с обратным знаком, т.е. .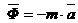

Если использовать понятие силы инерции, то основной закон динамики принимает вид: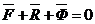

Принцип Даламбера. При движении материальной точки активные силы и силы реакции связей вместе с силой инерции точки образуют равновесную систему сил.

Принцип Даламбера называют еще методом кинетостатики. Задачи динамики с помощью этого метода сводятся к задачам статики.

Относительное движение материальной точки

Во многих задачах динамики движение материальной точки рассматривается относительно системы отсчета, движущейся относительно инерциальной системы отсчета.

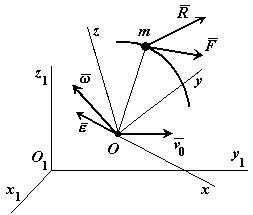
Получим дифференциальные уравнения движения материальной точки относительно подвижной системы отсчета.

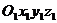- инерциальная система отсчета.

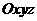- подвижная система отсчета.

,

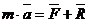где 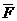- сумма активных сил, 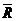- сумма сил реакции связи.

Согласно теореме Кориолиса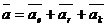

Перепишем дифференциальное уравнение следующим образом

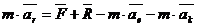
Введем обозначения

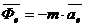- переносная сила инерции,

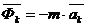- кориолисова сила инерции.

С учетом этих обозначений мы получаем динамическую теорему Кориолиса (уравнения относительного движения).

Материальная точка движется относительно неинерциальной системы отсчета так же как и относительно инерциальной, только к приложенным активным силам и силам реакции связей следует добавить кориолисову и переносную силу инерции.

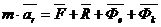
Силы 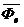и 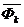являются поправками на неинерционность системы.

В проекциях на подвижные оси

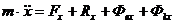
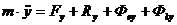
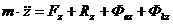
Количество движения точки

Количеством движения материальной точки 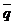называется вектор, равный произведению массы точки 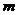на ее скорость .

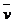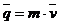
Количество движения точки в физике часто называют импульсом материальной точки.

Проекции количества движения точки на прямоугольные декартовы оси координат равны:

, ,

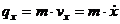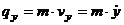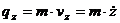
Единицей измерения количества движения в СИ является –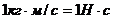

Теорема об изменении количества движения точки.

Теорема. Производная по времени от количества движения точки равна действующей на точку силе.

Запишем основной закон динамики 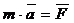в виде 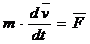. Так как масса постоянна, то внесем ее под знак производной.

Тогда , (*)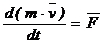

что и требовалось доказать.

В проекциях на координатные оси уравнение (*) можно представить в виде: