I. Волновые свойства упругих и электромагнитных волн

Физика

Лекция № 20

I. Волновые свойства упругих и электромагнитных волн

Лекции 4,5 Дифракция света

Это явление отклонения света от прямолинейного распространения, когда свет, огибая препятствия, заходит в область геометрической тени.

В общем случае дифракцию понимают как нарушение законов геометрической оптики, сопровождаемое интерференционными явлениями.

Природа и основные принципы дифракции могут быть установлены с помощью принципа Гюйгенса-Френеля.

4.1. Принцип Гюйгенса-Френеля

В 1678 г. Гюйгенс сформулировал правило, называемое принципом Гюйгенса: каждая точка, до которой доходит волна, является источником (центром) одной из вторичных волн, а огибающая этих волн задает положение волнового фронта в следующий момент времени. (Напомним, что волновым фронтом называется геометрическое место точек, до которых доходят колебания к моменту времени t).

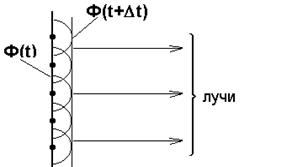Рис.1

Пусть Ф(t) – фронт волны в момент времени t (см. рис.1). Тогда, согласно принципу Гюйгенса, фронт волны в момент времени t+Dt совпадает с поверхностью огибающей всех вторичных волн. Основная слабость принципа Гюйгенса в том, что он не учитывает явления интерференции вторич- ных волн и, следовательно, не позволяет рассчитывать амплитуды волн, распространяющихся в различных направлениях.

Этот недостаток был устранен Френелем, который в 1815 г. дополнил принцип Гюйгенса, введя представление о когерентности вторичных волн и интерференции их между собой.

Дополненный Френелем принцип Гюйгенса называется принципом Гюйгенса-Френеля.

4.2. Метод зон Френеля

Расчет интерференции вторичных волн сводится к интегрированию, которое часто бывает затруднительным.

Для упрощения вычислений при определении амплитуды волны в заданной точке пространства Френель предложил разбивать поверхность фронта волны на зоны (зоны Френеля) так, что волны от соседних зон приходят в точку наблюдения в противофазе и, вычитаясь, ослабляют друг друга.

Применим метод зон Френеля для расчета дифракции света.

Различают два случая дифракции света:

1. Дифракция Френеля или дифракция в сходящихся лучах, когда на препятствие падает плоская или сферическая волна, и дифракционная картина наблюдается на экране, находящемся на конечном расстоянии от него (см. 4.3.)

2. Дифракция Фраунгофера или дифракция в параллельных лучах, когда на препятствие падает плоская волна, и дифракционная картина наблюдается на экране, который находится в фокальной плоскости собирающей линзы, установленной на пути прошедшего через препятствие света (см.4.4.)

4.3. Дифракция Френеля на круглом отверстии и диске

4.3.1. Дифракция Френеля на круглом отверстии

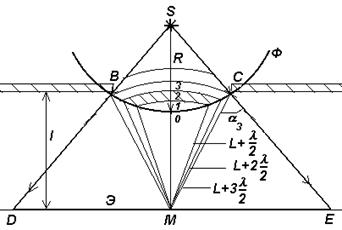L Рис.2

Сферическая волна, распространяющаяся из точечного источника монохроматического света S, встречает на своем пути экран с круглым отверстием, диаметр которого d=BC. Пусть Ф – фронт волны, который является частью поверхности сферы. Разобьем поверхность фронта на зоны Френеля (см. рис.2) так, что волны от соседних зон приходят в точку наблюдения М в противофазе. Тогда амплитуда результирующей волны в точке М

А=А₁-А₂+А₃-А₄+… А_m , (1)

где А_i – амплитуда волны, пришедшей от i-ой зоны Френеля. Перед А_m берется знак плюс, если m – нечетное, и минус, если m - четное.

Величина А_i зависит от площади s_i i-той зоны и угла a_i между внешней нормалью к поверхности зоны в какой-либо точке и прямой, направленной из этой точки в точку М (см. рис.2, где в частности показан угол a₃).

Можно показать, что все зоны Френеля примерно равновелики по площади. Увеличение же угла a_i с ростом номера зоны приводит к уменьшению амплитуды А_i. Она уменьшается с ростом i также и вследствие увеличения расстояния от зоны до точки М. Таким образом, А₁>А₂>…> A_m . При большом числе зон можно приближенно считать, что А_i=(A_i-1+A_i+1)/2. (2)

Перепишем теперь (1) в виде

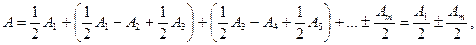(3)

так как согласно (2) все выражения, стоящие в скобках, равны нулю.

Можно показать, что общее число m зон Френеля, обращенное к точке М,

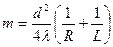, (4)

где d=BC – диаметр отверстия, R=SO, L=OM (см. рис.2), l- длина волны.

Если d=1 см, R=L=10 см и l=500 нм, то m=1000.

В этом случае А_m<<A₁ и слагаемым 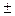А_m/2 в (3) можно пренебречь. Тогда согласно (3)

А=А₁/2. (5)

Таким образом, амплитуда результирующей волны в точке Мопределяется как бы действием только половины центральной зоны Френеля. Ее диаметр d, как следует из (4) при m=1, R=L=10 см и l=500 нм, равен 0,32 мм.

Следовательно, распространение света от S к М происходит так, будто пучок света распространяется внутри очень узкого канала вдоль SM, т.е. прямолинейно.

В этом случае круговое пятно диаметром ED (см. рис.2) равномерно освещено и вне его наблюдается тень. Следовательно, дифракционная картина отсутствует, когда диаметр отверстия BC=d>>l.

При уменьшении диаметра отверстия до величины d 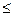1мм число зон согласно (4) уменьшается и А_m становится сравнимым с А_1, и поэтому пренебречь слагаемым 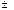А_m/2 в (3) нельзя.

При нечетном числе зон согласно (3)

А=А₁/2 +А_m/2 (6)

и в точке Мнаблюдается максимум (светлое пятно).

При четном числе зон

А=А₁/2 -А_m/2 (7)

и в точке М будет наблюдаться минимум (темное пятно). Этот факт особенно наглядно противоречит закону прямолинейного распространения света.

Очевидно, что максимум и минимум будут тем сильнее отличаться друг от друга, чем ближе значение А_m к А₁, т.е. когда число зон m мало (m 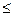10). Расчет амплитуды в других точках экрана более сложен. Можно показать, что дифракционная картина вблизи точки М имеет вид чередующихся темных и светлых колец с центрами в точке М. По мере удаления от точки Минтенсивность максимумов света убывает.

Если на пути световой волны в плоскости отверстия поставить зонную пластинку, которая перекрывала бы все четные зоны, то А=А₁+А₃+А₅+… и интенсивность I=A² в точке М резко возрастает. Еще большего эффекта можно достичь, не перекрывая четные зоны, а изменяя фазу их колебаний на p, тогда А=А₁+А₂+А₃+… Такая пластинка называется фазовой зонной пластинкой, и использование ее позволяет получить дополнительное увеличение интенсивности в 4 раза.

Опыт подтверждает эти выводы: зонная пластинка увеличивает интенсивность в точке М, действуя подобно собирающей линзе.

4.3.2. Дифракция Френеля на небольшом диске (круглом непрозрачном экране)

Способ построения зон Френеля на открытой части волнового фронта Ф падающей монохроматической волны показан на р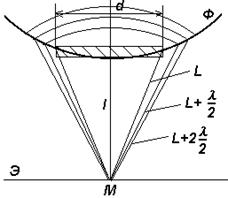ис.3.

Рис.3

Пусть диск закрывает несколько зон, действие которых не будем учитывать. Нумерацию зон начнем от первой открытой зоны, расстояние до краев которой от точки М равны L и L+l/2. Последнюю открытую зону обозначим через m. Проведя анализ, подобный предыдущему (см. 4.3.1), и полагая, что m достаточно велико, получим для амплитуды результирующей волны, выражение идентичное (5), т.е. А=А1/2. Дифракционная картина на экране Э имеет вид концентрических темных и

светлых колец с центром в точке М, где всегда находится максимум (пятно Пуассона).

4.4. Дифракция Фраунгофера на одной щели

Дифракция в параллельных лучах была рассмотрена Фраунгофером в 1821-1822 гг. Для получения пучка параллельных лучей света, падающих на щель или отверстие, обычно пользуются небольшим источником света, который помещается в фокусе собирающей линзы Л.

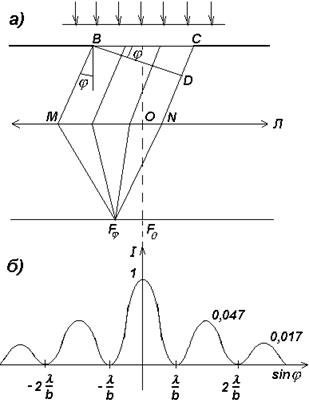Рис.4

Пусть параллельный пучок монохроматического света падает нормально на непрозрачный экран, в котором прорезана узкая щель ВС, имеющая постоянную ширину b и длину l>>b (см. рис.4,а). Оптическая разность хода между крайними лучами ВМ и CN, идущими от щели под углом j к оптической оси линзы OF0 D=CD=bsinj. Разобьем щель ВС на зоны Френеля, имеющие вид полос, параллельных ребру В щели. Ширина каждой зоны выбирается (согласно методу зон Френеля) так, чтобы разность хода от краев этих зон была равна l/2. При интерференции света от каждой пары соседних зон амплитуда результирующих колебаний равна нулю, так как эти зоны вызывают колебания с одинаковыми амплитудами, но противоположными фазами.Всего на ширине щели уместится D:

l/2= bsinj/(l/2) зон. Если число зон четное, т.е.

bsinj/(l/2)=±2m или bsinj=±ml , m=1,2,3…, (8)

то наблюдается дифракционный минимум (темная полоса).

Если число зон нечетное, т.е.

bsinj/(l/2)=±(2m+1) или bsinj=±(2m+1) 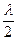, m=1,2,3…, (9)

то наблюдается дифракционный максимум (светлая полоса).

В направлении j=0 наблюдается самый интенсивный центральный максимум нулевого порядка.

Распределение интенсивности на экране, полученное вследствие дифракции (дифракционный спектр) приведено на рис.4,б. Расчеты показывают, что интенсивности в центральном и последующем максимумах относятся как 1:0,045:0,016:0,008:…, т.е. основная часть световой энергии сосредоточена в центральном максимуме.

Углы, под которыми наблюдаются максимумы всех порядков, начиная с первого, зависят от длины волны света l. Поэтому, если щель освещать немонохроматическим светом, то максимумы, соответствующие разным длинам волн, будут наблюдаться под разными углами и, следовательно, будут пространственно разделены на экране. Получим дифракционный спектр, в отличие от призматического спектра (см. дисперсию).

4.5. Дифракционная решетка

Дифракционная решетка – важнейший спектральный прибор, предназначенный для разложения света в спектр и измерения длин волн.

Она представляет собой плоскую стеклянную или металлическую поверхность, на которой нарезано очень много (до сотен тысяч) прямых равноотстоящих штрихов.

Рассмотрим простейшую идеализированную решетку, состоящую из N одинаковых равноотстоящих параллельных щелей, сделанных в непрозрачном экране. Ширину щели обозначим b, а ширину непрозрачных промежутков между щелями – а. Величина d=a+b называется периодом или постоянной дифракционной решетки. Лучшие решетки имеют d=0,8 мкм, т.е. 1200 штрихов на 1 мм.

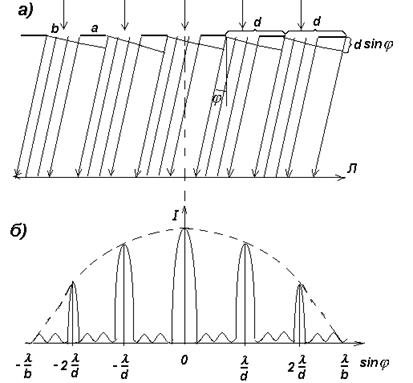Рис.5

На рис. 5а показано только несколько щелей. Дифракционная картина от решетки получается в результате дифракции на каждой щели и интерференции лучей, падающих от разных щелей. Главные максимумы соответствуют таким углам j, для которых колебания от всех N щелей складываются в фазе, т.е. Амакс=NAj, где Aj - амплитуда колебания, посылаемого одной щелью под углом j. Интенсивность максимума Iмакс=N2 Ij (10) т.е. может превышать в сотни миллионов раз интенсивность

максимума, создаваемого одной щелью (для хороших решеток N достигает нескольких десятков тысяч).

Условие главных максимумов имеет вид

dsinj=±ml , m=0,1,2… (11)

Максимум нулевого порядка наблюдается при j=0, первого порядка при sinj=±l/d, второго порядка при sinj=±2l/d (см. рис. 5,б)

Главные минимумы соответствуют таким углам j, в направлении которых ни одна из щелей не распространяет свет. Таким образом, условие главных минимумов выражает формула (8)

bsinj=±ml , m=1,2,3… (12)

Первый главный минимум наблюдается при sinj=±l/b (см. рис. 5,б).

Кроме главных максимумов имеется большое число слабых побочных максимумов, разделенных дополнительными минимумами. На рис. 5,б они изображены между главными максимумами.

Положение главных максимумов (кроме центрального) зависит от длины волны l [см. (11) и рис. 5,б]. Поэтому при пропускании через решетку белого света все максимумы ненулевого порядка, разложатся в спектр, фиолетовый конец которого обращен к центру дифракционной картины, а красный – наружу. Таким образом, дифракционная решетка представляет собой спектральный прибор.

4.6. Дифракция на пространственной решетке. Формула Вульфа-Брэгга

Дифракционную картину могут дать не только рассмотренные выше одномерные структуры, но также двумерные и трехмерные периодические структуры, например, кристаллические тела. Однако период кристаллических тел d мал, составляет единицы ангстрем (1 =10^-4 мкм), т.е. значительно меньше длин волн видимого света (l»0,4-0,8 мкм). Поэтому для видимого света кристаллы являются однородной средой, и дифракция не наблюдается.

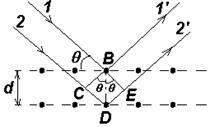Рис.6

В то же время для значительно более коротковолнового рентгеновского излучения(l »10-9 – 10-11 м) кристаллы представляют собой естественные дифракционные решетки (см. рис.6). Абсолютный показатель преломления всех сред для рентгеновского излучения близок к единице, поэтому оптическая разность хода между лучами

1’ и 2’, отражающимися от кристаллографических плоскостей D=CD+DE=2dsinq, где d – расстояние между плоскостями, в которых лежат узлы (атомы) кристаллической решетки, q - угол скольжения лучей.

Условию интерференционных максимумов удовлетворяет [см.(3,15)] формула Вульфа-Брэгга

2dsinq =±ml , m=1,2,3… (13)

где m – порядок дифракционного максимума.

4.7. Разрешающая способность оптических приборов

Вследствие дифракции света в оптическом приборе изображение светящейся точки имеет вид не точки, а светлого пятна, окруженного системой концентрических интерференционных колец. Это явление ограничивает разрешающую способность оптического прибора, т.е. его способность давать раздельное изображение двух близких друг к другу точек объекта.

Согласно критерию Рэлея, изображения двух одинаковых точечных источников света еще можно видеть раздельно, если центральный максимум дифракционной картины от одного источника совпадает с первым минимумом дифракционной картины от другого.

В этом случае угловое расстояние Dj 1,22l/D,

где D – диаметр объектива.

4.8. Понятие о голографии

При обычной фотографии фотопластинка регистрирует только интенсивность световой волны. Информация о фазе волны при этом теряется. Таким образом, содержащаяся в фотографии информация об объекте весьма ограничена, например, не можем увидеть то, что было закрыто во время съемки объектом, находящемся на переднем плане, - не можем заглянуть за этот объект.

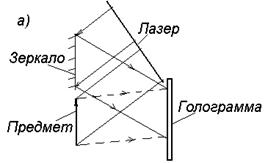	Голография (от греческого “полная запись“) позволяет записать на фотопластинку (голограмму) полную информацию (амплитуду и фазу) об объекте и затем восстановить изображение. Для этого необходимо иметь излучение с высокой степенью когерентности, полученное с помощью лазера. На рис.7 приведена схема получения
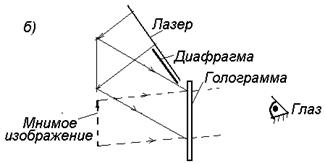Рис.7	голограммы (а) и восстановления изображения (б). Для получения цветного голографического изображения объекта пользуются монохроматическим светом трех основных цветов (например, красным, зеленым и синим), испускаемым одновременно тремя лазерами. Если голограмму расколоть на

несколько кусков, то каждый из них при просвечивании восстанавливает полное изображение, но с меньшей четкостью.

Физика

Лекция № 20

I. Волновые свойства упругих и электромагнитных волн