Учет значащих цифр при вычислениях

Значащими цифрами в десятичном изображении числа являются все цифры, кроме нулей, стоящих вначале числа. Нули в середине или в конце числа являются значащими. Например, в числе 0,04070 первые два нуля не являются значащими, а третий и четвёртый – значащие.

В случае записи больших чисел с нулями на конце (например, число 62000) возникает неопределённость, заключающаяся в том, что заранее не ясно, являются ли эти нули значащими цифрами, или же они служат только для определения разряда остальных цифр. Для устранения этой неопределённости такие числа следует записывать, например, в виде 6,2×10⁴, если значащими являются только две первые цифры, и 6,20×10⁴, если значащими являются три цифры и т.д.

Если полученное приближенное значение физической величины содержит лишние (незначащие) или недостоверные цифры, то его округляют.

Правила округления:

1) при сложении и вычитании в результате сохраняют столько десятичных знаков, сколько их содержится в числе с наименьшим количеством десятичных знаков;

2) при умножении и деления в результате сохраняют столько значащих цифр, сколько их имеет приближенное число с наименьшим количеством значащих цифр;

3) результат расчета значений функций (xⁿ, 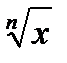, lgx и т.п.) числа x должен содержать столько значащих цифр, сколько их имеется в числе x.

Окончательный результат обязательно проводится вместе с погрешностью и всегда записываются так, чтобы их последние цифры принадлежали к одному и тому же десятичному разряду. Нельзя писать 18 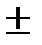0,4 или 18,32 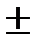0,4. Правильная запись: 18,3 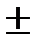0,4.

Построение графиков. Отражение доверительных интервалов на графиках

Обычно с помощью линейки или лекала через экспериментальные точки проводится гладкая кривая таким образом, чтобы сумма квадратов расстояний от точек до кривой была минимальной.

Рис. 1. Диаграмма с экспериментальных точек погрешности

x

y

На графиках погрешности указываются для одной или обеих измеряемых величин в виде отрезков длиной в доверительный интервал (рис. 1), в центре которых расположены экспериментальные точки (или в виде прямоугольника, стороны которого равны доверительным интервалам). В зависимости от того, пройдет ли теоретическая кривая (прямая) через доверительные интервалы экспериментальных точек, результаты эксперимента признают согласующимися или не согласующимися с теорией.

Однако через построенные точки можно, в принципе, провести несколько прямых с немного отличающимся наклоном (или же несколько кривых, если функциональная зависимость нелинейная). Для повышения точности результатов в тех случаях, когда заранее известен вид функциональной зависимости двух величин (линейная, логарифмическая, экспоненциальная или степенная), следует воспользоваться методом наименьших квадратов.

3. ЛАБОРАТОРНЫЕ РАБОТЫ