Тангенциальное, нормальное и полное ускорение материальной точки.

Вектор ускорения можно представить в виде двух составляющих:

-Тангенциальной

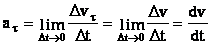т. е. равной первой производной по времени от модуля скорости: она характеризует быстроту изменения скорости по модулю (направлена по касательной к траектории) Вектор аτ направлен в сторону движения точки при возрастании ее скорости и в противоположную сторону - при убывании скорости

-Нормальной

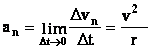характеризующей быстроту изменения скорости по направлению (направлена к центру кривизны траектории). Поэтому ее называют так же центростремительным ускорением.

Полное ускорение есть геометрическая сумма тангенциальной и нормальной составляющих:

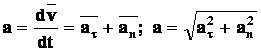
ß модуль полного ускорения (последняя формула)

Тангенциальная и нормальная составляющие взаимно перпендикулярны.

!!8.Угловая скорость движения материальной точки по окружности.

Угловой скоростью вращения называется вектор, численно равный первой производной угла поворота тела по времени и направленный вдоль оси вращения по правилу правого

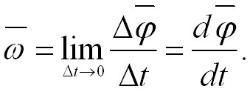Единица измерения угловой скорости радиан в секунду (рад/с) – угловая скорость равномерно вращающегося тела, все точки которого за время 1 с поворачиваются относительно оси на угол 1 рад.

Угловое ускорение.

Для характеристики неравномерного вращения тела вводится понятие углового ускорения. Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени:

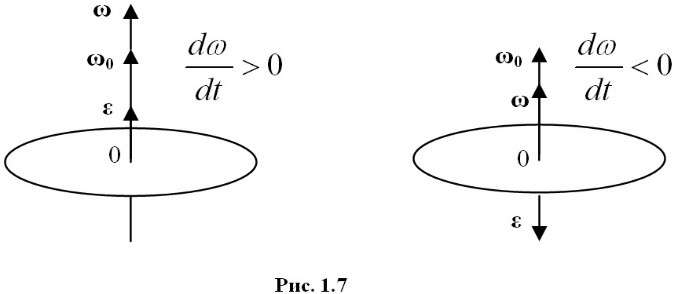
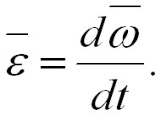
При вращении тела вокруг неподвижной оси вектор углового ускорения направлен вдоль оси вращения в сторону вектора угловой скорости (рис. 1.7); при ускоренном движении вектор ε направлен в ту же сторону, что и ω (dω/dt > 0), и в противоположную сторону при замедленном вращении (dω/dt < 0).

Связь между линейными и угловыми величинами.

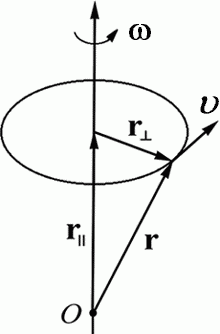
Угловая скорость может быть связана с линейной скоростью υ произвольной точки А. Пусть за время Δt точка проходит по дуге окружности длину пути Δs. Тогда линейная скорость точки будет равна:

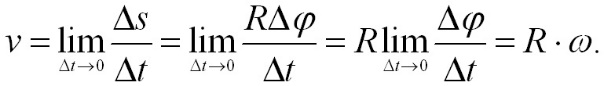
Положение рассматриваемой точки задается радиус-вектором r, который проводится из лежащего на оси вращения начала координат О. Из рисунка следует, что R = rsin a, следовательно:

v = sin a

Первый закон Ньютона.

Он также известен как Закон инерции. Инерция — это свойство тела сохранять скорость своего движения неизменной (и по величине, и по направлению), когда на тело не действуют никакие силы.

В современной формулировке: Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальные точки, когда на них не действуют никакие силы (или действуют силы взаимно уравновешенные), находятся в состоянии покоя или равномерного прямолинейного движения.

В исторической формулировке: Всякое тело продолжает удерживаться в состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние.