Средняя и мгновенная скорость движения материальной точки.

Скорость – это векторная физическая величина, введенная для определения быстроты движения и его направления в данный момент времени.

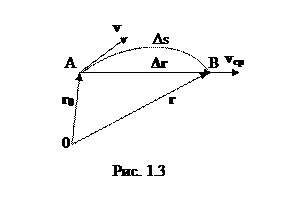Физическая величина, равная отношению вектора перемещения 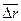к промежутку времени, за который это перемещение произошло называется средней скоростью материальной точки за промежуток времени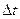

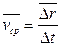
Вектор 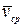направлен так же, как 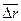, т е направлен вдоль хорды, стягивающей участок траектории 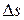. В случае прямолинейного движения в одном направлении =

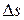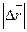
Модуль средней скорости определяется как отношение пути ∆S, пройденного телом за некоторый промежуток времени, к этому промежутку:

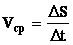
Мгновенная скорость 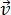есть предел, к которому стремится средняя скорость 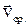, когда промежуток времени движения стремится к нулю:

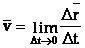
Мгновенная скорость 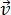есть векторная величина, равная первой производной радиуса - вектора движущейся точки по времени. Так как секущая в пределе совпадает с касательной, то вектор скорости 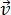направлен по касательной к траектории в сторону движения.

По мере уменьшение ∆t путь ∆S все больше будет приближаться к 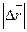, поэтому модуль мгновенной скорости:

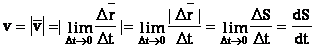
Таким образом, модуль мгновенной скорости 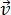равен первой производной пути по времени :

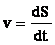
Путь, пройденный материальной точкой при равномерном и равнопеременном движении.

Если выражение ds = vdt проинтегрировать по времени в пределах от t до t+Δt, то найдем длину пути, пройденного точкой за время Δt:

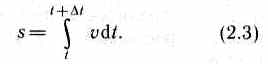
В случае равномерного прямолинейного движения число­вое значение мгновенной скорости

посто­янно; тогда выражение примет вид

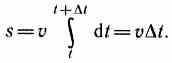
Длина пути, пройденного точкой за промежуток времени от t1 до t2, дается интегралом

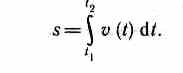
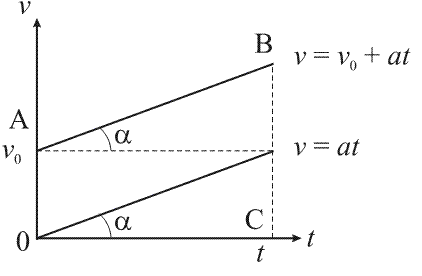
Равнопеременным движением (равноускоренным или равнозамедленным) называется такое движение, при котором модуль скорости за любые равные интервалы времени изменяется (увеличивается или уменьшается) на равную величину. При равнопеременном прямолинейном движении вектор ускорения – величина постоянная.

График зависимости модуля скорости равнопеременного движения от времени движения Средняя скорость равна:

.

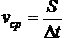По графику скорости можно найти путь за интервал времени 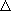t. Он численно равен площади трапеции ОАВС:

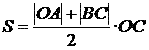, где

|OA| = v₀, |BC| = v, OC = t.

Подставим эти значения и получим:

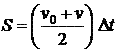
Подставим формулу модуля скорости

v = v₀ ± a 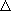t. И получается:

Формула пути равнопеременного движения

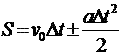
Среднее и мгновенное ускорение материальной точки.

Средним ускорением неравномерного движения в интервале от t до t + ∆t называется векторная величина, равная отношению изменения скорости ∆v к интервалу времени ∆t:

Мгновенным ускорением ав момент времени t будет предел среднего ускорения:

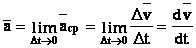
Ускорение ∆а есть векторная величина, равная первой производной скорости по времени.