Расчет газопроводов при большихбольших перепадах давлений

При движении газа в трубопроводе постоянного диаметра одновременно изменяются давление, плотность и скорость движения. Так, давление уменьшается из-за необходимости совершать работу по преодолению силы трения, плотность также уменьшается (при изотермическом течении она пропорциональна давлению). Средняя скорость движения газа увеличивается по ходу его движения, так как массовый расход остается постоянным, а плотность падает. Таким образом, использовать в явном виде уравнение Бернулли для несжимаемой жидкости использовать нельзя.

Выберем два бесконечно близких сечения. Так, как в этих счениях плотность газа фактически не меняется, то можно для этих сечений записать уравнение Бернулли для несжимаемой жидкости. Значение слагаемых во втором сечении уравнения Бернулли равны z₂ = z₁ + dz, p₂ = p₁ + dp, a v₁²/2g = a v₂²/2g + da v₁²/2g. Тогда уравнение Бернулли запишется:

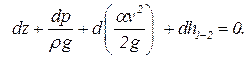(4.19)

Для газопроводов первое и третье в Уравнение Бернулли гораздо меньше остальных двух слагаемых, поэтому ими пребрегаем. Местными потерями можно пренебречь. Умножая уравнение (4.20) получим:

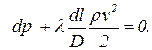(4.20)

Кроме уравнения (4.20), необходимо уравнение неразрывности потока:

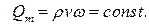(4.21)

А также зависимость плотности газа от давления:

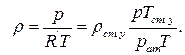(4.22)

где r_ст.у - плотность газа при стандартных условиях, кг/м³;

T_ст.у - температура газа при стандартных условиях, K.

Потери на трение и коэффициент трения l=f(Re, D_э/d) определяются по тем же формулам, что и для несжимаемой жидкости.

Докажем, что при изотермическом течении, когда постоянна вязкость, по длине трубы число Re не изменяется.

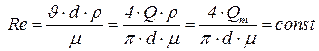(4.23)

Следовательно, коэффициент трения также постоянен по длине трубопровода.

Исключив из уравнений (4.20), (4.21) и (4.22) плотность газа и скорость получим:

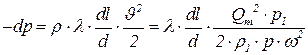(4.24)

Разделяем переменные, учитываем, что w =p×d²/4, интегрируем и получаем следующие расчетные формулы:

Определение давления при известном расходе

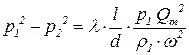(4.25)

Определение массового расхода при известных давлениях р₁ и р₂:

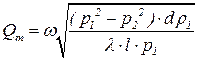(4.26)

4.7.2. Пример расчета

Воздух при t=2°C движется по трубопроводу диаметром d=0,1м и длиной 15км. Давление в начале трубопровода 4,41Мпа, а в конце 0,29 Мпа. Определить массовый расход. Трубопровод изготовлен из новых стальных сварных труб.

Решение задачи.

Используем формулу (53).

Здесь неизвестны плотность газа в начале трубопровода r₁ и коэффициент трения.

Определяем плотность газа в начале трубопровода.

r₁ =р₁/RT =4,41×10⁶/287/275=56,6кг/м³.

Здесь R=287 – газовая постоянная для воздуха, T=273+2=275 –абсолютная температура.

Предполагаем турбулентный режим движения, задаемся величиной

l =0,02 и вычисляем в первом приближении массовый расход:

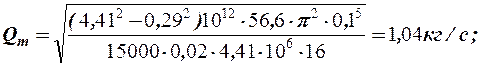
Определяем число Re и режим движения газа.

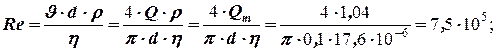
Коэффициент динамической вязкости определяем с помощью Приложения 3.

При р=98кПа и t=2°C - n=13,9×10^-6м²/с, плотность r=1,27кг/м³, следовательно:

h = n×r = 13,9×10^-6 × 1,27 = 17,6×10^-6 Па×с.

Уточняем значение коэффициента трения. При турбулентном режиме:

l=0,11(68/Re+D_э/d)^0,25 = 0,11(68/7,5×10⁵ +0,1×10^-3/0,1)^0,25 = 0.0199=0,02.

Для новых стальных сварных труб D_э =0,1мм.

Таким образом, значение коэффициента трения практически не изменилось и массовый расход газа определен правильно.