Движение неньютоновских жидкостей в трубах
При движении вязкой ньютоновской жидкости по круглой трубе в соответствии с законом вязкого трения Ньютона (1.9) касательное напряжение t пропорционально градиенту скорости и(r ), т.е.
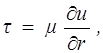 (10.1)
(10.1)
где r — текущий радиус.
Величина h = ¶ u/¶ r называется скоростью сдвига и уравнение (10.1) записывается в виде
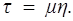 (10.2)
(10.2)
При этом считается, что при температуре Т = const динамический коэффициент вязкости m = const.
Уравнение (10.2) представляет собой простейший пример реологического уравнения жидкости. Это уравнение содержит единственный реологический параметр - динамический коэффициент вязкости. Наиболее простой классификацией неньютоновских жидкостей является классификация, в которой неньютоновские жидкости группируются по трем основным категориям.
1. Неньютоновские вязкие жидкости, для которых скорость сдвига зависит только от приложенных напряжений, т.е.
h = f(t). (10.3)
2. Жидкости, для которых скорость сдвига определяется не только величиной касательного напряжения, но и продолжительностью его действия.
3. Вязкоупругие жидкости, проявляющие одновременно вязкость и упругость.
Неньютоновские вязкие жидкости делятся на две группы:
а) жидкости, обладающие начальным напряжением сдвига t0, т.е. жидкости, которые начинают течь лишь после того, как касательное напряжение превысит некоторый предел t0;
б) жидкости, не обладающие начальным напряжением сдвига t0.
Примером жидкости группы а) является вязкопластичная жидкость. Ее реологическое уравнение имеет вид
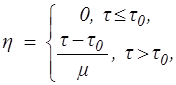 (10.4)
(10.4)
т.е. при t £ t0 среда ведет себя как твердое тело.
Величина m называется коэффициентом пластической вязкости.
Примером жидкостей группы б) являются степенные или нелинейно-вязкие жидкости. Их реологическое уравнение имеет вид
t = k hn,
где k — консистентность; n —индекс течения.
Зависимость касательного напряжения от скорости сдвига называется кривой течения.
Кривые течения степенных жидкостей проходят через начало координат. При п < 1 жидкость называется псевдопластичной, а при п > 1 - дилатантной.
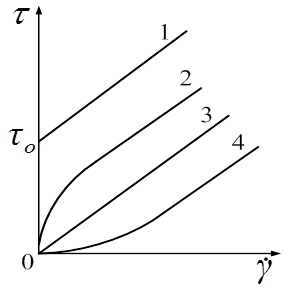
Рис. 10.1. Кривые течения неньютоновских вязких жидкостей
На рис. 10.1 приведены кривые течения неньютоновских вязких жидкостей. Кривая 1 соответствует вязкопластичной жидкости, кривая 2 —псевдопластичной, кривая 4 —дилатантной; кривая 3 соответствует случаю п = 1, т.е. представляет собой кривую течения для вязкой жидкости.
Для неньютоновских вязких жидкостей вводится понятие кажущейся вязкости
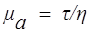 (10.5)
(10.5)
и текучести
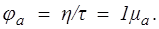 (10.6)
(10.6)
В отличие от ньютоновской жидкости величины mа и jа — не константы, а функции касательного напряжения.
При движении неньютоновской вязкой жидкости по трубе радиусом а и длиной l под действием перепада давления Dp распределение касательного напряжения по радиусу, как и в случае ньютоновской жидкости, имеет вид
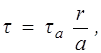 (10.7)
(10.7)
где tа — касательное напряжение на стенке трубы, определяемое из соотношения:
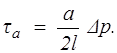
Распределение скорости по сечению трубы определяется по формуле
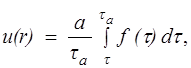 (10.8)
(10.8)
где f(t) определяется по формуле (10.3).
Расход неньютоновской вязкой жидкости определяется при любом виде функции f(t) из соотношения
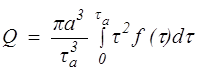 . (10.9)
. (10.9)
Формулы (10.6) и (10.7) справедливы при отсутствии пристенного скольжения. При вращательном течении неньютоновской вязкой жидкости между двумя соосными цилиндрами распределение касательного напряжения по радиусу имеет вид
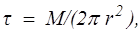 (10.10)
(10.10)
где М — момент сил трения, действующих на единицу длины цилиндра.
Угловая скорость наружного цилиндра W при отсутствии пристенного скольжения и неподвижном внутреннем цилиндре определяется по формуле
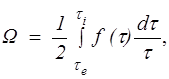 (10.11)
(10.11)
где ti , te — напряжения сил трения на поверхностях внутреннего и наружного цилиндра соответственно.
Вопросы по теме 10.
1. Как определяется неньютоновская жидкость?
2. Какая жидкость называется неньютоновской вязкой?
3. Каким реологическим уравнением описывается течение вязко-пластичной жидкости?
4. Сколько реологических параметров определяют модель степенной жидкости?
5. Как распределяется касательное напряжение по радиусу кольцевого зазора при вращательном течении жидкости?
6. К каким особенностям в распределении скорости по сечению трубы приводит наличие начального напряжения сдвига в модели вязко-пластичной жидкости?
Приложения
Приложение 1
Значения эквивалентной шероховатости для труб (по А.Д. Альтшулю)1
| Трубы | Состояние труб | Δ, мм |
| 1. Тянутые из стекла и цветных металлов 2. Бесшовные стальные 3. Стальные сварные 4. Чугунные | Новые, технически гладкие Новые и чистые После нескольких лет эксплуатации Новые и чистые С незначительной коррозией после очистки Умеренно заржавевшие Старые заржавевшие Новые асфальтированные Новые без покрытия Бывшие в употреблении Очень старые | 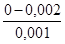 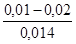 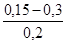 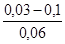 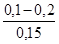 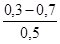 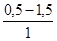 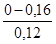 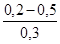 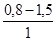 до 3 мм до 3 мм |
1В знаменателе – среднее значение D
Приложение 2
Значения усредненных коэффициентов местных сопротивлений (квадратичная зона)
| Сопротивление | ζкв | Сопротивление | ζкв |
| Вход в трубу: с острыми кромками вдающийся внутрь резервуара Выход из трубы Угольник с углом поворота: 45О 90О Колено плавное (90О) Тройник Шаровой кран Вентиль обычный Прижимная коробка трубы с клапаном и сеткой при dтр, мм: | 0,5 1,00 1,00 0,44 1,32 0,23 0,32 45,00 4,00 7,00 6,00 5,20 3,70 | Задвижка: полностью открытая (n=1) n=0,75 n=0,5 n=0,4 n=0,3 n=0,2 Кран пробковый Фильтры для нефтепродуктов: светлых темных Диафрагма с острыми кромками при n= Sот/Sтр: 0,4 0,5 0,6 0,7 | 0,15 0,20 2,00 4,60 10,00 35,00 0,40 1,70 1,20 7,00 4,00 2,00 0,97 |
Приложение 3.
Поправочная функция j для zкв в формуле z= jzкв
при ламинарном и переходном режимах движения
| Re | j | Re | j |
| 4,20 3,81 3,51 3,37 3,22 3,12 3,01 | 2,95 2,90 2,84 2,48 2,26 2,12 1,98 |
Приложение 4.
Теплофизические свойства некоторых жидкостей
| Свойство | Температура, оС | ||||||||
| Вода | |||||||||
| Плотность r, кг/м3 Динамическая вязкость h, мПа×с Давление насыщенных паров pп, кПа | 1,31 1,22 | 1,00 2,34 | 0,80 4,24 | 0,66 7,38 | 0,55 12,34 | 0,47 19,92 | 0,41 31,17 | 0,36 47,37 | 0,32 70,13 |
| Топливо Т-1 | |||||||||
| Плотность r, кг/м3 Динамическая вязкость h, мПа×с Давление насыщенных паров pп, кПа | –– –– –– | 1,49 4,67 | –– 7,47 | 1,08 11,21 | –– 15,61 | 0,83 21,35 | –– 28,02 | 0,66 36,02 | –– 44,43 |
| Масло МС-20 | |||||||||
| Плотность r, кг/м3 Динамическая вязкость h, мПа×с | 248,0 | 102,0 | 47,5 | 24,0 | 13,4 | 8,0 | 5,1 | 3,5 | 2,4 |
II. Задания для выполнения контрольных работ студентами – заочниками
Вариант 1
Номера контрольных задач выбираются согласно последней цифре шифра зачетной книжки студента (см. табл. 1.1), числовые значения указанных в задаче величин – по предпоследней цифре шифра зачетной книжки студента (табл. 1.2).
Таблица 1.1.
