Электронные орбиты некоторых атомов

(масштабный чертеж в соответствии с теорией Бора)

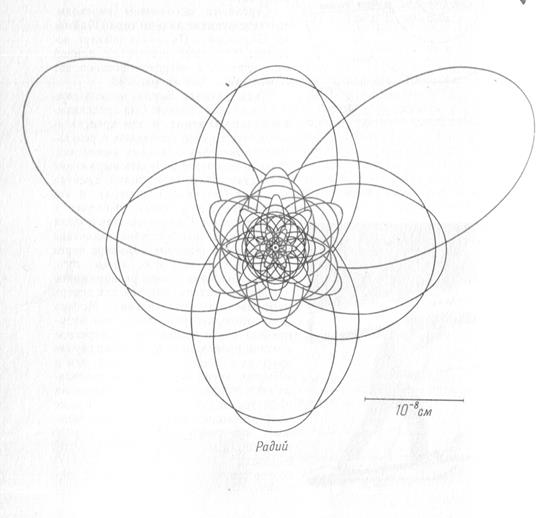
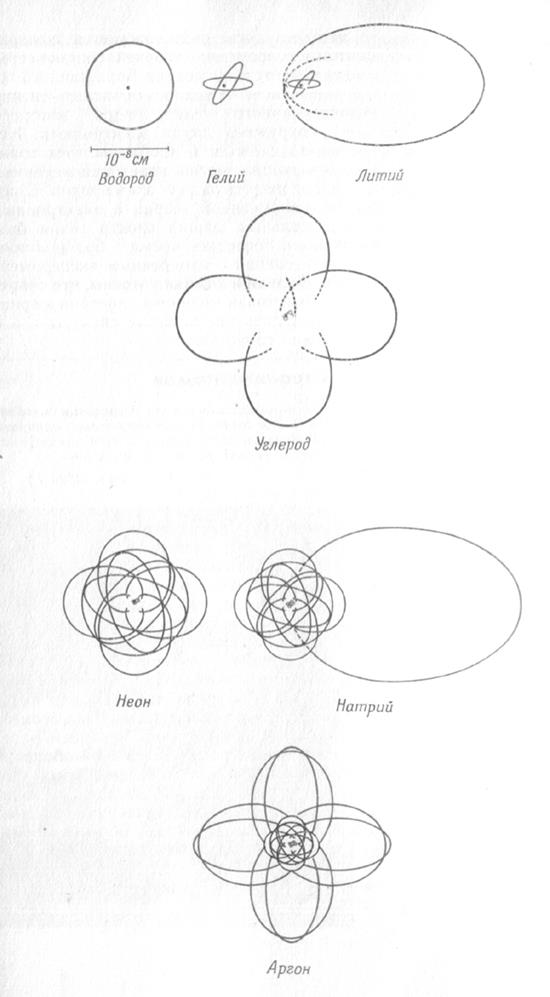
Бор использовал для описания состояния электрона законы классической механики и электростатики, которые не выполняются для движения электрона в атоме. Также не объясняет теория Бора мгновенный переход электрона с одной орбиты на другую.

Эти противоречия устранены в теории квантово-механического описания состояния атома.

Она основана на развитии представлений Эйнштейна и Планка.

Из уравнений (1) и (2) получаем 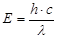(3)

Согласно уравнению Эйнштейна энергия фотона связана с массой : 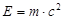(4)

Из (3) и (4) получаем

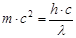или 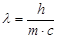, отсюда следует, что фотону свойственна двойная природа - частицы и волны.

Распространение представлений о двойственности природы фотона на природу других микрообъектов, в том числе и электрона, легло в основу создания теории квантово-механического объяснения строения атома.

Де Бройль высказал предположение о двойственной природе электрона, т.е. для электрона массой m и скоростью v

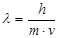- уравнение де Бройля

Наличие волновых свойств у электрона было подтверждено экспериментально.

Основываясь на двойственной природе электрона, Шрёдингер в 1925 г. предположил, что состояние движущегося в атоме электрона должно описываться известным в физике уравнением стоячей электромагнитной волны. Подставив в это уравнение вместо длины волны ее значение из уравнения де Бройля, он получил новое уравнение, связывающее энергию с пространственными координатами и так называемой волновой функцией ψ, которая в этом уравнении соответствует амплитуде трехмерного волнового процесса.

Уравнение Шрёдингера является дифференциальным уравнением в частных производных. Для стационарного состояния 1 частицы массой m:

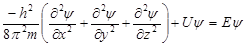
Ĥ – Гамильтон

U – потенциальная энергия;

Е – полная энергия

h - постоянная Планка

ψ– волновая функция

х, у, z - координаты

ψ– волновая функция, ее физический смысл состоит в том, что

ψ²dv – вероятность нахождения рассматриваемой частицы в элементарном объеме dv

ψ² - плотность вероятности или, если речь идет об электроне, - электронная плотность.

В соответствии с физическим смыслом ψ, она должна быть конечной, непрерывной и однозначной, а также обращается в ноль в тех местах пространства, где частица не может находиться, например, ψ=0 для электрона, находящегося на бесконечно большом расстоянии от ядра.

Из уравнения Шрёдингера находят Е и зависимость ψ(ψ²) от координат, т.е. распределение вероятности пребывания частицы в пространстве, в частности распределение электронной плотности в атоме.

Решение уравнения Шрёдингера приводит всегда к определенному набору дозволенных значений энергии электронов Е (квантование энергии).

Понятия квантовой механики резко отличаются от классической механики.

Квантовая механика:

определяет вероятность нахождения частицы в атоме (также массы, энергии, момента импульса).

Классическая механика:

определяет траекторию движения, координаты частицы или скорость ее движения в определенный момент времени.

Квантовая механика вместо понятия "движение электрона" использует понятие "состояние электрона", т.е. движение электрона в атоме образует "электронное облако", плотность которого в различных точках определяется плотностью вероятности ψ² и составляет орбиталь электрона.

Одно из основных положений квантовой механики - соотношение неопределенностей Гейзенберга (1927 г.):

невозможно точно определить местоположение частицы и ее импульс

p = m·v в данный момент времени.

Δх ·Δр_х ≥ћ; ћ =h/2π; ΔР_х=m∙ΔV_x

Δх - неопределенность положения частицы (ошибка определения ее координаты х в данный момент времени)

ΔР_х, ΔV_x - неопределенности составляющих импульса и скорости в направлении координаты х.

При решении уравнения Шрёдингера (для атома водорода) в полярной системе координат получают ψ в виде произведения трех функций, каждая из которых содержит только одну переменную.

ψ(r,Q,φ)=R(r)∙Q(θ)∙Φ(φ)

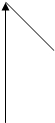Q – угол широты

φ – угол долготы

r

Q

y

φ

Проекция радиуса вектора

на плоскости ху

х

Наличие трех степеней свободы движения электрона приводит к тому, что в решении уравнения Шредингера для атома водорода проявляются 3 величины, которые могут принимать только целочисленные значения - три квантовых числа.

n= 1.....∞

l= 0,1,2......(n-1)

m_l= 0, ±1; ±2,.... ±l

Для других (более сложных атомов) еще одно квантовое число m_s=±1/2

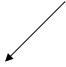
Расчет по уравнению Шредингера позволяет определить помимо энергии электрона размер и форму электронного облака. Некоторые из форм орбиталей приведены на рисунках ниже.

z

1s l = 0

у

х

z z z

2p_y 2p_x 2р_z

у

y у

х

х х