Молекулярно-кинетическая теория газов

1. При повышении температуры газа на Dt₁ = 180 °С среднеквадратичная скорость молекул возрастает от < u_кв1 > = 400 м/с до < u_кв2 > = 500 м/с. На сколько градусов Dt₂ надо нагреть газ, чтобы увеличить среднеквадратичную скорость молекул от < u_кв2 > = 500 м/с до < u_кв3 > = 600 м/с?

2. В течение Dt = 0,1с на стенку перпендикулярно ее поверхности со скоростью u = 800 м/с падает пучок молекул азота, количество вещества в котором n = 1 моль. Молекулы отскакивают перпендикулярно стенке без потери энергии. Определить силу давления F пучка на стенку. Молярная масса азота m = 0,028 кг/моль.

3. Найти число молекул кислорода в 1 см³ и среднее расстояние
между ними как функции давления p при температуре T, построить графики этих функций.

4. Вычислить среднюю квадратичную скорость и среднюю кинетическую энергию поступательного движения молекулы азота как функции температуры T, построить графики этих функций.

5. Определить температуру газа, для которой средняя скорость
молекул азота отличается от их наиболее вероятной скорости на Du = 300 м/с.

6. В сосуде находится масса m₁ = 14 г азота (M₁ = 28×10 ^{– 3} кг/моль) и масса m₂ = 9 г водорода (M₂ = 2×10 ^{– 3} кг/моль) при температуре t = 10 °С и давлении p = 1 МПа. Найдите молярную массу M смеси и объем V сосуда.

7. Считая воздух газом, состоящим из одинаковых молекул, определите среднеквадратичную скорость < u_кв > молекул при нормальных условиях, если плотность воздуха при нормальных условиях r = 1,3 кг/м³.

8. Сколько молекул N газа находится в сосуде вместимостью V = 480 см³ при температуре t = 20 °С и давлении p = 2,5×10⁴ Па?

9. Двухатомный газ массой m = 2 кг находится под давлением p = 5×10⁵ Па и имеет плотность r = 4,0 кг/м³. Найдите энергию Е теплового движения газа при этих условиях.

10. На какой высоте давление воздуха составляет 60 % от давления на уровне моря? Считать, что температура воздуха везде одинакова и
равна t = 10 °С.

11. Определить отношение давления воздуха на высоте h = 1 км и давление на дне скважины глубиной h = 1 км. Воздух у поверхности
Земли находится при нормальных условиях, а его температура не зависит от высоты.

12. На высоте 1 км в 1 см³ воздуха содержится примерно 104 пылинки, у поверхности Земли – примерно 105. Определить среднюю массу пылинки и оценить ее размер, предполагая, что плотность пылинки 1,5 г/см³, средняя температура воздуха равна 27 °С.

13. Найдите среднюю длину свободного пробега молекул азота при нормальных условиях. Диаметр молекулы принять равным d = 3×10 ^{– 8} см. Молярная масса азота M = 2,8×10 ^{– 2} кг/моль.

14. В закрытом сосуде емкостью 2 м³ находятся 1,4 кг азота и 2 кг кислорода. Найти давление газовой смеси в сосуде, если температура
смеси t = 27 °C.

15. Сухой атмосферный воздух содержит 23,1 % кислорода (от общей массы), 75,6 % азота и 1,3 % аргона. Доля остальных газов пренебрежимо мала. Определить среднюю молярную массу сухого атмосферного воздуха.

16. Найти среднюю длину свободного пробега молекул воздуха при температуре 20 °C и давлении 1,5×10⁵ Па. Эффективный диаметр молекул воздуха принять равным 0,3×10 ^{– 9} м.

17. Подсчитать количество столкновений, которые испытывает за 1 с молекула аргона при температуре 290 К и давлении 0,1 мм рт. ст. Эффективный диаметр молекулы аргона равен 2,9×10 ^{– 10} м.

18. Каковы средняя квадратичная и средняя арифметическая скорости пылинки массой 0,1 г, находящейся в воздухе во взвешенном состоянии при температуре 17 °С?

19. Во сколько раз средняя квадратичная скорость молекул водорода больше средней квадратичной скорости молекул водяных паров при той же температуре?

20. При какой температуре молекулы аргона имеют такую же среднюю квадратичную скорость, как молекулы гелия при 100 К?

21. Определить среднюю арифметическую скорость молекул газа, если их средняя квадратичная скорость 600 м/с.

22. Какова наиболее вероятная скорость молекул метана и гелия при температуре 127 °С?

23. Какая часть молекул азота при температуре 7 °С обладает скоростями в интервале от 500 до 510 м/с?

24. Какая часть молекул кислорода обладает скоростями, отличающимися от наиболее вероятной не более чем на 10 % при температуре 0 °С?

25. Два одинаковых баллона соединены трубкой с клапаном, пропускающим газ из одного баллона в другой при разности давлений Dp ³ 1,10 атм. Сначала в одном баллоне был вакуум, а в другом – идеальный газ при температуре t = 27 °С и давлении p₁ = 1,00 атм. Затем оба баллона нагрели до температуры t₂ = 107 °С. Каким стало давление газа в баллоне, где был вакуум?

26. Определить наименьшее возможное давление идеального газа в процессе, происходящем по закону T = T₀ + a V ², где T₀ и a – положительные постоянные; V – объем одного моля газа. Изобразить примерный график этого процесса в параметрах p, V.

27. Сосуд объемом V = 20 л содержит смесь водорода и гелия при температуре t = 20 °C и давлении p = 2,0 атм. Масса смеси m = 5,0 г. Найти отношение массы водорода к массе гелия в данной смеси.

28. Найти максимально возможную температуру идеального газа в следующем процессе: p = p₀ - a V ², где p₀, a – положительные постоянные; V – объем моля газа.

29. Найти максимально возможную температуру идеального газа в следующем процессе: p = p₀ e^{-b V}, где p₀, b – положительные постоянные; V – объем моля газа.

30. При какой температуре T₁ находился газ, если при нагревании его на Dt = 60 °C при постоянном давлении его объем увеличится на 15 %?

31. Открытую пробирку с воздухом при атмосферном давлении медленно нагрели до некоторой температуры T₁, затем герметически закрыли и охладили до t₂ = 14 °C. Давление воздуха при этом упало на 30 %. До какой температуры была нагрета пробирка?

32. Горизонтально расположенный цилиндрический сосуд делится на две части подвижным поршнем. Каково отношение объемов цилиндра, разделенных поршнем, если одну часть сосуда заполнить кислородом, а другую часть – такой же массой водорода (температура T = const)? При каком отношении температур кислорода T₁ и водорода T₂ поршень
будет делить цилиндр на равные части?

33. Металлический баллон с кислородом хранится в помещении, где температура воздуха t₁ = 24 °C. При этом манометр показывает давление p₁ = 0,23 МПа. Когда баллон вынесли на улицу, где температура t₂ = - 12 °C, манометр показал p₂ = 0,19 МПа. Определить, произошла ли утечка газа за время, прошедшее между двумя измерениями давления. Атмосферное давление p₀ = 0,1 МПа.

34. В сосуде при температуре T находится газ под давлением p₁ = 1,6×10⁶ Па. Определить давление газа в сосуде после того, как три четверти массы газа выпущено из сосуда, а температура возросла в два раза (T₂ = 2 T₁).

35. Определить плотность r смеси, состоящей из m₁ = 4 г водорода и m₂ = 32 г кислорода, при температуре t = 27 °C и давлении p = 10⁵ Па.

36. Стеклянная трубка, внутренний объем которой V = 15 см³, была нагрета до T₁ = 723 К, после чего ее горизонтально опустили в ртуть, имеющую температуру T₂ = 290 К на небольшую глубину так, что воздух остается внутри трубки. Определить массу ртути m вошедшей внутрь трубки. Плотность ртути r = 1,36×10⁴ кг/м³.

37. Масса m = 12 г газа занимает объем V = 4 л при температуре t₁ = 70 °C. После нагревания газа при постоянном давлении его плотность стала равной r = 0,6 кг/м³. До какой температуры t₂ нагрели газ?

38. Перед проведением газосварочных работ манометр баллона с кислородом показывал давление p₁ = 10 МПа, а после сварки p₂ = 8 МПа. Сколько кислорода (%) было израсходовано? Температура и объем кислорода в баллоне не изменились.

39. Светильный газ подают по газопроводу при давлении p = 0,4 МПа и температуре T = 300 К, причем через поперечное сечение трубы площадью S = 0,8×10 ^{– 2} м² за время t = 120 с прошло m = 8,4 кг газа. Определить среднюю скорость u газа в газопроводе. Молярная
масса газа M = 16,4×10 ^{– 3} кг/моль.

40. При нагревании газа на ΔT при постоянном давлении его объем увеличился на 1 / N от первоначального объема. Найти начальную температуру газа.

Термодинамика

41. Один моль идеального газа изохорически перевели из состояния 1 в состояние 2, при этом давление уменьшилось в n = 1,5 раза. Затем газ изобарически нагрели до первоначальной температуры T₁ = 300 К. Какую работу совершил газ в результате этих переходов?

42. Какой газ подвергался изотермическому сжатию и чему равен его первоначальный удельный объем, если давление 2 кг газа в конце сжатия увеличилось в три раза, и работа, затраченная на сжатие, равна 1,370∙10³ кДж? До сжатия газ находился под давлением 5∙10⁵ Па и имел температуру 27 °C.

43. 2 кмоля углекислого газа нагреваются при постоянном давлении на 50 °C. Найти: а) изменение его внутренней энергии; б) работу расширения; в) количество тепла, сообщенного газу.

44. При изотермическом расширении 10 г азота, находящегося при температуре 17 °C, была совершена работа 860 Дж. Во сколько раз изменилось давление азота при расширении?

45. Работа изотермического расширения 10 г некоторого газа от объема V₁ до V₂ = 2 V₁ равна 575 Дж. Найти среднюю квадратичную скорость молекул газа при этой температуре.

46. При изотермическом расширении 2 м³ газа давление его меняется от p₁ = 5 атм до p₂ = 4 атм. Найти совершенную при этом работу.

47. 7,5 л кислорода адиабатно сжимаются до объема 1 л, причем в конце сжатия устанавливается давление 1,6∙10⁶ Па. Под каким давлением газ находился до сжатия?

48. Воздух в цилиндрах двигателя внутреннего сгорания сжимается адиабатно, и его давление при этом изменяется от p₁ = 1 атм до p₂ = 35 атм. Начальная температура воздуха 40 °C. Найти температуру воздуха в конце сжатия.

49. Двухатомный газ, находящийся при температуре 27 °C и давлении 2∙10⁶ Па, сжимается адиабатно от объема V₁ до объема V₂ = 0,5 V₁. Найти температуру и давление газа после сжатия.

50. В сосуде под поршнем находится гремучий газ, занимающий при нормальных условиях объем 10 ^{– 4} м³. При быстром сжатии газ воспламеняется. Найти температуру воспламенения газа, если известно, что работа сжатия равна 46,35 Дж.

51. Двухатомный газ занимает объем V₁ = 0,5 л при давлении p₁ = 0,5 атм. Газ сжимается адиабатно до некоторого объема V₂ и давления p₁, затем при постоянном объеме V₂ охлаждается до первоначальной температуры. При этом давление его становится равным p₀ = 1 атм.
а) Начертить график этого процесса. б) Найти объем V₂ и давление p₂.

52. Газ расширяется адиабатно так, что его давление падает от 2 до 1 атм, затем нагревается при постоянном объеме до первоначальной температуры, при этом его давление возрастает до 1,22 атм. а) Определить отношение с_p / c_V газа. б) Начертить график процесса.

53. Один киломоль азота, находящегося при нормальных условиях, расширяется адиабатно от объема V₁ до объема V₂ = 5 V₁. Найти: а) изменение внутренней энергии газа; б) работу, совершенную при расши­рении.

54. Необходимо сжать 1∙10 ^{– 2} м³ воздуха до объема 2∙10 ^{– 3} м³. Как выгоднее производить сжатие: адиабатно или изотермически? Найти отношение работы, производимой газом при этих процессах.

55. Кислород массой 10 г, находящийся при нормальных условиях, сжимается до объема 1,4∙10 ^{– 3} м³. Найти давление и температуру кислорода, если он сжимается: а) изотермически; б) адиабатно. Найти работу
сжатия в каждом из этих случаев.

56. Два различных газа, один из которых одноатомный, а другой двухатомный, находятся при одинаковой температуре и занимают одинаковый объем. Газы сжимаются адиабатно так, что объем их уменьшается в два раза. Какой из газов нагреется больше и во сколько раз?

57. Воздух массою 1 кг, находящийся при температуре 30 °C и давлении 1,5 атм, расширяется адиабатно, его давление при этом падает до 1 атм. Найти: а) степень расширения; б) конечную температуру; в) работу, совершенную газом при расширении.

58. В водонагревателе нагрели V = 50 л воды, имевшей температуру t₁ = 20 °C, до температуры t₂ = 80 °C и сожгли для этого m = 6,3 кг дров. Найти коэффициент полезного действия водонагревателя h. Удельная теплота сгорания дров q = 10 МДж/кг, удельная теплоемкость воды c = 4,2 кДж/(кг∙К), ее плотность r = 10³ кг/м³.

59. Какое количество фреона m должно испариться для замерзания V = 0,5 л воды с начальной температурой T₁ = 288 К, если коэффициент полезного действия холодильной установки h = 0,8. Температура кристаллизации воды T₂ = 273 К, удельная теплота плавления льда l = 3,32×10⁵ Дж/кг, удельная теплота испарения фреона r = 1,68×10⁶ Дж/кг, удельная теплоемкость воды c = 4,2×10³ Дж/(кг∙К), плотность воды r = 10³ кг/м³.

60. С какой скоростью летела свинцовая пуля, если при ударе о стенку она расплавилась наполовину? Температура пули до удара T₁ = 400 К, во внутреннюю энергию пули превращается h = 0,8 ее кинетической энергии. Удельная теплоемкость свинца c = 130 Дж/(кг∙К); удельная теплота плавления свинца l = 2,4×10⁴ Дж/кг; температура плавления T₂ = 600 К.

61. Определить мощность P двигателя автомобиля с КПД h = 0,3, если при скорости u = 20 м/с двигатель потребляет объем V = 10 л бензина на пути S = 100 км. Удельная теплота сгорания бензина q = 44 МДж/кг, его плотность r = 7×10² кг/м³.

62. На электроплитке мощностью N = 600 Вт, имеющей КПД h = 45 %, нагрели m = 1,5 кг воды, взятой при t₁ = 10 °C, до кипения и 5 % (h₁ = 5 %) ее обратили в пар. Удельная теплота парообразования воды r = 2,2 МДж/кг, удельная теплоемкость воды c = 4,2 кДж/(кг∙К). Найти время процесса.

63. Вода в чайнике, поставленном на электроплиту, закипает через время t₁ = 5 мин. За какое время t₂ она затем полностью испарится, если первоначальная температура воды была t = 20 °C? Удельная теплоемкость воды c = 4,2 кДж/(кг∙К); удельная теплота парообразования воды r = 2,2 МДж/кг.

64. В двигателе внутреннего сгорания при работе образуются газы, температура которых t₁ = 727 °C. Температура отработанного газа t₂ = 127 °C. Двигатель расходует за время t = 30 мин m = 18 кг топлива, удельная теплота сгорания которого q = 4,2×10⁷ Дж/кг. Найти полезную мощность двигателя. Считать, что двигатель работает по идеальному циклу Карно.

65. При уменьшении объема кислорода от V₁ = 20 дм³ до V₂ = 10 дм³ его давление возросло от p₁ = 0,10 МПа до p₂ = 0,25 МПа. Каково приращение внутренней энергии газа?

66. В цилиндре под поршнем находится двухатомный газ в количестве n = 1,0 моль при температуре t₁ = 27 °C. Сначала газ расширяется адиабатно так, что объем увеличился в k = 5 раз, а затем сжимается изотермически до первоначального объема. Определить совершенную газом работу A.

67. Газ, для которого с_p / c_V = 4/3, находится под давлением p = 0,20 МПа и занимает объем V = 3,0 дм³. В результате изобарного
нагревания объем его увеличился в k = 3 раза. Определить количество теплоты Q, переданное газу.

68. Плотность некоторого газа при нормальных условиях r = 1,25 кг/м³. Отношение удельных теплоемкостей g = 1,4. Определить удельные теплоемкости с_p и c_V этого газа.

69. Газ, совершающий цикл Карно, КПД которого h = 25 %, при изотермическом расширении производит работу A₁ = 240 Дж. Какова
работа A₂, совершаемая газом при изотермическом сжатии.

70. Идеальный газ совершает цикл Карно. Температура нагревателя T₁ = 470 К, а температура холодильника T₂ = 280 К. При изотермическом расширении газ совершает работу A = 100 Дж. Определить термический КПД цикла, а также количество теплоты Q₂, которое газ отдает холодильнику при изотермическом сжатии.

71. Тепловая машина работает по циклу Карно. Температура нагревателя t₁ = 327 °C. Определить КПД цикла и температуру T₂ холодильника тепловой машины, если за счет Q₁ = 2 кДж теплоты, полученной от нагревателя, машина совершает работу A = 400 Дж.

72. Во сколько раз необходимо увеличить объем n = 5 моль идеального газа при изотермическом расширении, если его энтропия увеличилась на DS = 57,6 Дж/К?

73. Идеальный газ (n = 2 моль) сначала изобарно нагревали так, что объем увеличился в n = 2 раза, а затем изохорно охладили, так что давление его уменьшилось в k = 3 раза. Определить приращение энтропии DS в ходе указанных процессов.

74. Азот массой m = 28 г (M = 28×10 ^{– 3} кг/моль) адиабатически расширили в n = 2 раза, а затем изобарно сжали до первоначального объема. Определить изменение энтропии DS газа в ходе указанных процессов.

75. Кусок льда массой 1 кг, взятый при температуре – 20 °С был нагрет и расплавлен, а затем при атмосферном давлении полученная вода доведена до кипения и превращена в пар. Найти полное изменение энтропии данной массы вещества.

76. Стальной шар массой 10 кг при температуре 500 °С погружается в сосуд с 18 кг воды, температура которой 15 °С. Найдите изменение энтропии системы в процессе установления равновесного состояния в предположении адиабатности системы. Теплоемкость стали 0,5129 кДж/(кг×К).

77. Определите изменение энтропии в процессе испарения 2 кг воды при нормальном давлении, если известно, что теплота парообразования r = 2257 кДж/кг.

78. Средняя теплоемкость алюминия в интервале температур от 0 до 300 °С равна 0,955 кДж/(кг×К). Определите энтропию 200 кг алюминия при 300 °С, считая, что его энтропия при 0 °С равна нулю.

79. Докажите, что цикл из двух изохор V₁ и V₂ и двух изотерм T₁ и T₂ имеет КПД, меньший, чем КПД цикла Карно, протекающего при тех же предельных температурах.

80. Найти КПД цикла Клапейрона, состоящего из двух изотерм
T₁ = const, T₂ = const (T₁ > T₂) и двух изохор V₁ = const, V₂ = const (V₂ > V₁).

Реальные газы

81. В сосуде вместимостью V = 10 л находится азот массой m = 0,25 кг. Определить: 1) внутреннее давление p¢ газа; 2) собственный объем V ¢ молекул.

82. Криптон, содержащий количество вещества n = 1 моль, находится при температуре Т = 300 К. Определить относительную погрешность Dp / p, которая будет допущена при вычислении давления, если вместо уравнения Ван-дер-Ваальса воспользоваться уравнением Менделеева – Клапейрона. Вычисления выполнить для двух значений объема:
1) V = 2 л; 2) V = 0,2 л.

83. Давление кислорода равно 7 МПа, его плотность r = 100 кг/м³. Найти температуру кислорода, считая газ ван-дер-Ваальсовcким.

84. В закрытом сосуде объемом V = 0,5 м³ находится n = 0,6 кмоль углекислого газа при давлении р = 3 МПа. Пользуясь уравнением Ван-дер-Ваальса, найти, во сколько раз надо увеличить температуру газа, чтобы давление увеличилось вдвое.

85. Какому давлению необходимо подвергнуть углекислый газ при Т = 300 К, чтобы его плотность оказалась равной r = 500 г/л? Расчет
провести как для идеального газа, так и для ван-дер-ваальсовского.

86. Один моль некоторого газа находится в сосуде объемом V = 0,250 л. При T₁ = 300 К давление газа р₁ = 90 атм, а при T₂ = 350 К давление р₂ = 110 атм. Найти постоянные Ван-дер-Ваальса для этого газа.

87. Найти плотность гелия в критическом состоянии, считая его
ван-дер-ваальсовским газом. Значения критических параметров Т_К = 5,2 К, р_К = 0,23∙10⁶ Па.

88. Критическая температура аргона Т_К = 151 К, давление р_К = = 4,86 МПа. Определить по этим данным критический объем V_К аргона.

89. Газ находится в критическом состоянии. Во сколько раз возрастет давление р газа, если его температуру Т изохорически увеличить в n = 2 раза? Использовать уравнение Ван-дер-Ваальса в приведенной
форме.

90. Найти давление p ¢, обусловленное силами взаимодействия
молекул одного киломоля газа при нормальных условиях. Критические температура и давление этого газа равны Т_К = 417 К и р_К = 7,7 МПа.

91. Определить внутреннюю энергию одного моля азота при критической температуре Т_К = 126 К. Вычисления выполнить для четырех значений объемов: 1) 20 л; 2) 2 л; 3) 0,2 л; 4) V_К.

92. Найти внутреннюю энергию углекислого газа массой m = 132 г при нормальном давлении p₀ и температуре Т = 300 К в двух случаях, когда газ рассматривается как: 1) идеальный; 2) реальный.

93. Определить изменение внутренней энергии одного моля неона при изотермическом расширении от объема V₁ = 1 л до V₂ = 2 л.

94. Объем углекислого газа массой m = 0,1 кг увеличился от V₁ = 103 л до V₂ = 104 л. Найти работу внутренних сил взаимодействия молекул при этом расширении газа.

95. В сосуде вместимостью V₁ = 1 л содержится m = 10 г азота. Определить изменение DТ температуры азота, если он расширяется в пустоту до объема V₂ = 10 л.

96. Газообразный хлор массой m = 7,1 г находится в сосуде вместимостью V₁ = 0,1 л. Какое количество теплоты Q необходимо подвести к хлору, чтобы при расширении его в пустоту до объема V₂ = 1 л
температура газа осталась неизменной?

97. Моль кислорода, занимавший первоначально объем V₁ = 1 л при температуре t₁ = 100 °С, расширился изотермически до V₂ = 10 л. Найти: 1) приращение внутренней энергии DU; 2) работу А, совершенную газом (сравнить А с работой A_ид, вычисленной по формуле для
идеального газа); 3) количество теплоты Q, полученное газом.

98. Получить для ван-дер-ваальсовского газа уравнение адиабаты в переменных V и Т. Сравнить полученные уравнения с аналогичными уравнениями для идеального газа.

99. Получить для ван-дер-ваальсовского газа уравнение адиабаты в переменных V и р. Сравнить полученные уравнения с аналогичными уравнениями для идеального газа.

100. Построить график зависимости внутренней энергии U моля ван-дер-ваальсовского газа от температуры Т при V = const. Сравнить эту зависимость с аналогичной для идеального газа.

101. Построить график зависимости внутренней энергии U моля ван-дер-ваальсовского газа от объема V при T = const. Сравнить эту
зависимость с аналогичной для идеального газа.

102. Найти выражение для энтропии моля ван-дер-ваальсовского
газа (как функцию от T и V). Сравнить с выражением для энтропии идеального газа.

Конденсированные состояния

103. Какую силу F нужно приложить к горизонтальному алюминиевому кольцу высотой h = 10 мм, внутренним диаметром d₁ = 50 мм и внешним диаметром d₂ = 26 мм, чтобы оторвать его от поверхности воды? Какую часть найденной силы составляет сила поверхностного натяжения?

104. Кольцо с внутренним диаметром d₁ = 50 мм и внешним диаметром d₂ = 26 мм подвешено на пружине и соприкасается с поверхностью жидкости. Жесткость пружины k = 9,8×10 ^{– 7} Н/м. При опускании
поверхности жидкости кольцо оторвалось от нее при растяжении пружины на 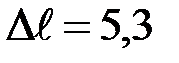мм. Найти поверхностное натяжение жидкости.

105. Масса 100 капель спирта, вытекающего из капилляра, равна 0,71 г. Определить поверхностное натяжение спирта, если диаметр шейки капли в момент отрыва равен 1 мм.

106. Трубка имеет диаметр d₁ = 0,2 см. На нижнем конце трубки повисла капля воды, имеющая в момент отрыва вид шарика. Найти диаметр d₂ этой капли.

107. При плавлении нижнего конца вертикально подвешенной свинцовой проволоки диаметром d = 1 мм образовалось N = 20 капель свинца. На сколько укоротилась проволока? Поверхностное натяжение жидкого свинца s = 0,47 Н/м. Диаметр шейки капли в момент обрыва считать равным диаметру проволоки.

108. С какой минимальной высоты должна упасть капля радиуса R, чтобы она разбилась на n одинаковых маленьких капель? Температура жидкости не меняется.

109. Какую работу нужно совершить, чтобы, выдувая мыльный пузырь, увеличить его диаметр от d₁ = 1 см до d₂ = 11 см? Процесс считать изотермическим.

110. На сколько нагреется капля ртути, полученная от слияния двух капель радиусом r = 1 мм каждая?

111. Воздушный пузырек диаметром d = 2 мкм находится в воде у самой ее поверхности. Определить плотность r воздуха в пузырьке, если воздух над поверхностью воды находится при нормальных условиях.

112. На сколько давление p воздуха внутри мыльного пузыря больше атмосферного давления p₀, если диаметр пузыря d = 5 мм?

113. Найти давление p воздуха в воздушном пузырьке диаметром d = 0,1 мм, находящемся на глубине h = 20 см под поверхностью воды. Атмосферное давление p₀ = 101,7 кПа.

114. Во сколько раз плотность воздуха в пузырьке, находящемся на глубине h = 5 м под водой, больше плотности воздуха при атмосферном давлении p₀ = 101,3 кПа? Радиус пузырька r = 0,5 мкм.

115. Водомерка бегает по поверхности воды. Найти массу водомерки, если известно, что под каждой из шести лапок насекомого образуется ямка, равная полусфере радиусом r = 0,1 мм.

116. В сосуд с ртутью опущен открытый капилляр, внутренний диаметр которого d = 3 мм. Разность уровней ртути в сосуде и в капилляреDh = 3,7 мм. Найти радиус кривизны R мениска в капилляре.

117. Каким должен быть внутренний диаметр d капилляра, чтобы при полном смачивании вода в нем поднималась на Dh = 2 см? Задачу решить, когда капилляр находится: а) на Земле; б) на Луне.

118. Капилляр с внутренним радиусом r = 2 мм опущен в жидкость. Найти коэффициент поверхностного натяжения жидкости, если
известно, что масса поднявшейся в капилляре жидкости m = 0,09 г.

119. В сосуд с водой опущен капилляр, внутренний радиус которого r = 0,16 мм. Каким должно быть давление р воздуха над жидкостью, чтобы уровень воды в капилляре и в сосуде был одинаков? Атмосферное
давление p₀ = 101,3 кПа. Смачивание считать полным.

120. Будет ли плавать на поверхности воды жирная (полностью несмачиваемая водой) платиновая проволока диаметром d = 1 мм?

Библиографический список

1. Савельев И. В. Курс общей физики. В 3 т. Т. 1. Механика. Молекулярная физика. – 5-е изд., стереотип. – СПб.: Лань, 2006. – 432 с.

2. Савельев И. В. Курс общей физики. В 3 т. Т. 2. Электричество и магнетизм. Волны. Оптика. – 5-е изд., стереотип. – СПб.: Лань, 2006. – 496 с.

3. Савельев И. В. Курс общей физики. В 3 т. Т. 3. Квантовая оптика. Атомная физика. Физика твердого тела. Физика атомного ядра и элементарных частиц. – 4-е изд., стереотип. – СПб.: Лань, 2006. – 304 с.

4. Рогачев Н. М. Курс физики: Учебное пособие. – СПб.: Лань, 2008. – 448 с.

5. Пиралишвили Ш. А. и др. Механика. Электромагнетизм / Ш. А. Пиралишвили, Н. А. Мочалова, З. В. Суворова, Е. В. Шалагина, В. В. Шувалов. – М.: Машиностроение, 2006. – 336 с.

6. Пиралишвили Ш. А. и др. Колебания. Волны. Геометрическая и волновая оптика. Квантовая и ядерная физика / Ш. А. Пиралишвили, Н. А. Мочалова, З. В. Суворова, Е. В. Шалагина, В. В. Шувалов. – М.: Машиностроение-1, 2007. – 341 с.

7. Пиралишвили Ш. А. и др. Термодинамика и молекулярная физика. Элементы статистической физики. Элементы физики конденсированного состояния / Ш. А. Пиралишвили, Н. А. Каляева, З. В. Суворова, Е. В. Шалагина, В. В. Шувалов. – М.: Машиностроение-1, 2008. – 348 с.

8. Пиралишвили Ш. А. и др. Молекулярная физика. Термодинамика. Конденсированные состояния: Учебное пособие / Ш. А. Пиралишвили, Е. В. Шалагина, Н. А. Каляева, Е. А. Попкова. – Рыбинск: РГАТА имени П. А. Соловьева, 2009. – 170 с.

9. Пиралишвили Ш. А. и др. Физические основы механики: Учебное пособие / Ш А. Пиралишвили, Е. В. Шалагина, Н. А. Каляева, Е. А. Попкова. – Рыбинск: РГАТУ имени П. А. Соловьева, 2013. – 148 с.

ПРИЛОЖЕНИЕ