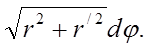Вычисление длины дуги кривой

Вычисление длин дуг кривых. Пусть кривая 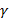задана параметрическими уравнениями x=x(t), y=y(t), z=z(t), t 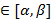, и функции x(t), y(t), z(t) непрерывно дифференцируемы на [ 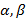]. Тогда кривая 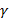спрямляема, и ее длина s может быть вычислена по формуле

.

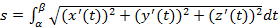Если кривая плоская (z =0), то

.

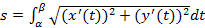Если кривая 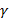является графиком непрерывно дифференцируемой функции y=f(x), 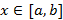, то

.

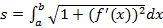Если кривая 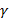задана в полярных координатах r=r( 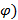, , 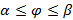то

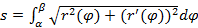[5].

Длина дуги линии – предел периметра ломаной линии, вписанной в данную дугу, если число звеньев этой линии неограниченно возрастает, а длина дуги каждого звена стремится к нулю. Для непрерывных линий упомянутый предел всегда существует, конечный или бесконечный. Если этот предел конечный, то линия (дуга ее) называется спрямляемой. В зависимости от способа аналитического задания линий длина дуги вычисляется по следующим формулам:

для плоских линий:

1) 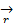= 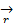(t), ;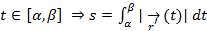

2) ;

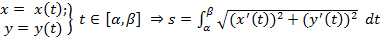3) ;

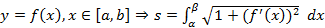4) ;

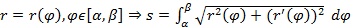для пространственных линий:

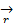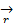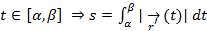5) = (t), ;[5]

Длина дуги кривой. Пусть плоская кривая AB задана уравнением y=f(x), a≤x≤b, где f(x) – непрерывная функция на отрезке [a,b]. Разобьем кривую AB на n произвольных частей точками 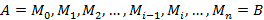в направлении от A к B. Соединив соседние точки хордами, получим некоторую вписанную в кривую AB ломаную, длину которой обозначим через P (рис 17). Через 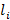обозначим длину одного звена 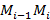ломаной, а через ϻ - длину наибольшего из ее звеньев: .

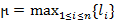Рисунок. 7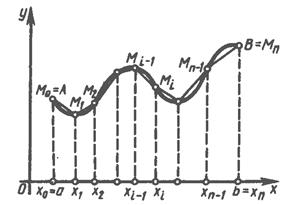

Определение. Число L называется пределом длин ломаных P при 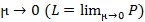, если для любого 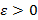существует 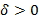такое, что для всякой ломаной, у которой 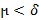, выполняется неравенство

.

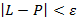Если существует предел L длин P вписанных в кривую ломаных при ϻŠ0, то этот предел называется длиной дуги AB.

Если функция f(x) непрерывна вместе с 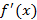на отрезке [a,b], то длина L дуги AB выражается формулой

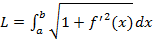. (1)

Доказательство. Обозначим через 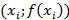координаты точки 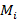, так что для абсцисс этих точек получим: 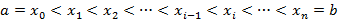. Тогда длина 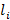одного звена ломаной равна

.

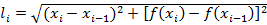По формуле Лагранжа

.

.

.

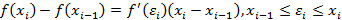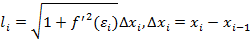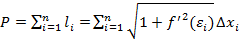Правая часть равенства представляет собой интегральную сумму для интеграла (1). Функция 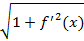непрерывна на [a,b], поэтому предел этой суммы при 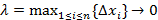существует и равен определенному интегралу (1). Так как 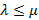, то 𝜆Š0 при 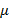Š0. Следовательно,

.

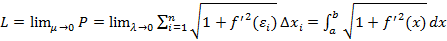Замечание 1. Для вычисления длины дуги в случае, когда кривая AB задана параметрическими уравнениями 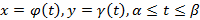, где 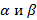- значения параметра t, соответствующие значениям x=a и x=b, т.е. a= 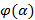, b= 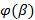в формуле 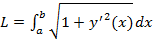надо сделать замену переменной, положив 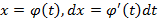. Тогда получим

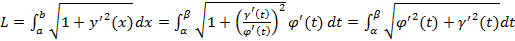. (2)

Замечание 2. Для вычисления длины дуги в случае, когда кривая AB задана полярных координатах уравнением 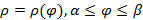, где 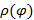имеет непрерывную производную 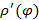на отрезке [ 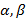], и точками A и B соответствуют значениям 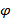, равные 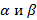, нужно перейти от полярных координат к прямоугольным. Тогда получим параметрическое задание кривой AB уравнениями 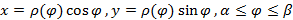( 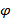- параметр). Так как

,

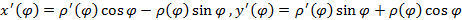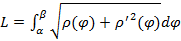. [5]

Полярные координаты. Пусть кривая AB задана уравнением в полярных координатах r = r( 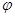), 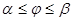. Предположим, что 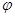r( ) и r 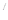( 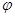) непрерывны на отрезке [ ].

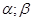Если в равенствах x = r cos 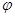, y = r sin 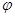, связывающих полярные и декартовы координаты, параметром считать угол 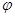, то кривую AB можно задать параметрически

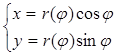
Тогда

= =

=

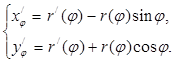
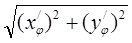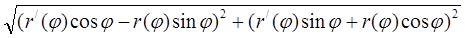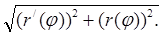
Рисунок. 8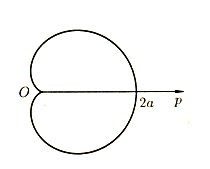

Применяя формулу

L = 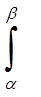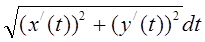, получаем

L =