Понятие определенного интеграла. Взаимосвязь неопределенного интеграла и определенного интегралов. Формула Ньютона-Лейбница. Свойства определенного интеграла.

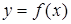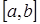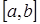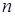Пусть функция определена на отрезке . Разобьем отрезок на частей точками 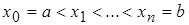. Выберем на каждом из полученных отрезков 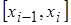произвольную точку .

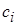Интегральной суммой функции 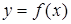на отрезке 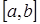называется сумма

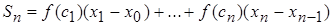или

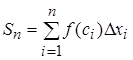, где .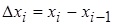

Наибольшую из длин 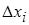обозначим через .

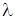Определенным интегралом функции 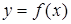на отрезке 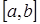называется число, равное пределу интегральной суммы 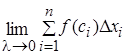и обозначается 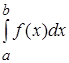, т.е.

.

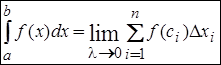Из условия 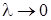следует, что .

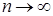Пределами интегрирования называются числа 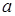и .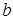

Подынтегральной функцией называется функция .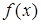

Если функция 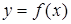непрерывна на отрезке 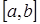, то определенный интеграл 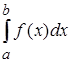существует.

Подчеркнем, что определенный и неопределенный интегралы существенно различаются между собой. Если неопределенный интеграл представляет семейство функций, то определенный - есть определенное число.

Свойства определенного интеграла

1. Постоянный множитель можно выносить за знак интеграла

.

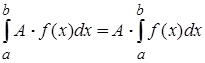2. Интеграл от алгебраической суммы двух функций равен сумме интегралов от этих функций (верно для любого числа слагаемых):

.

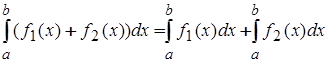3. При перемене порядка интегрирования знак определенного интеграла меняется на противоположный:

.

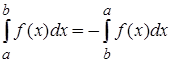4. Если отрезок интегрирования разбит на части, то интеграл на всем отрезке равен сумме интегралов для каждой из возникших частей, т.е. при любых а, b и с справедливо

.

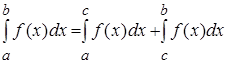5. Обе части неравенства можно почленно интегрировать, т.е. если для всех 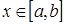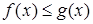, то

.

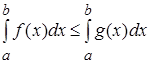6. Для 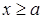определенный интеграл 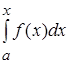становится функцией от переменного верхнего предела 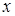. Производная этой функции равна значению подынтегральной функции в точке :

.

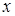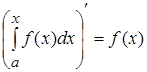7. Теорема о среднем. Если функция 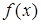непрерывна на 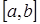, то существует точка 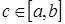такая, что

.

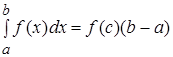Значение 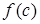называется средним значением функции 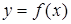на .

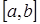у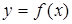

В

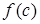
А

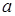
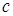
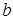
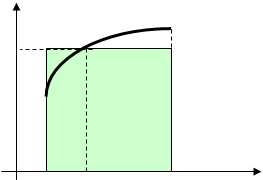
Площадь криволинейной трапеции 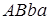равна площади прямоугольника с основанием 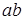и высотой, равной значению функции 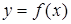в точке .

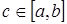Геометрически теорема о среднем означает, что на отрезке найдется такая точка, что площадь под кривой 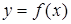на этом отрезке будет равна площади прямоугольника со сторонам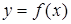и и .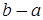

Формула Ньютона-Лейбница

Формула Ньютона-Лейбница связывает неопределенный и определенный интегралы.

Если функция 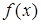непрерывна на 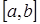, а функция 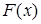- одна из ее первообразных, т.е. 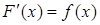, то определенный интеграл от функции f(х) на [а, b] равен приращению первообразной F(х) на этом отрезке, то есть

.

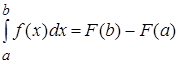Эта формула сводит нахождение определенного интеграла к нахождению неопределенного интеграла.

Разность 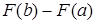называется приращением первообразной и обозначается .

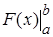Подчеркнем, что при применении формулы Ньютона-Лейбница можно использовать любую первообразную для подынтегральной функции, например, имеющую наиболее простой вид при С = 0 (в дальнейшем не будем записывать константу при нахождении неопределенного интеграла, поскольку будем считать ее равной нулю).

Пример 1. Вычислить определенный интеграл .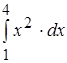

Решение. По формуле Ньютона-Лейбница имеем

.
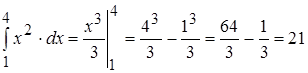