Элементарные сведения о микроскопе

Глаз, невооружённый никаким оптическим приспособлением, на расстоянии наилучшего зрения (25см) различает мелкие структурные образования (точки и линии) на поверхности тела или внутри прозрачного образца с разрешением (при расстоянии между ними) 0,08мм. Для того, чтобы рассматривать предметы с более мелкими деталями (структурой), нужно увеличить угол, под которым они наблюдаются (угол зрения). Этого можно достичь с помощью лупы или микроскопа.

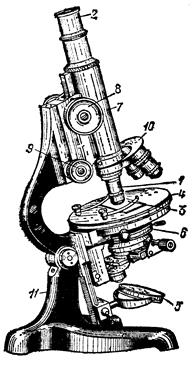
Рис. 1.1. Микроскоп

На рис. 1.1 представлен микроскоп. Основные части оптической системы микроскопа – объектив 1 и окуляр 2 – размещаются на концах цилиндрической трубки, укрепленной в штативе. Исследуемый объект 3 помещается на предметном столике 4 и освещается снизу с помощью зеркала 5 и конденсора 6. Оправы объектива и окуляра устанавливаются в металлической трубке – тубусе 7. Наводка на резкое изображение осуществляется с помощью микрометрического винта кремальеры 8 (грубая наводка) или микрометрического винта 9 (точная наводка). Окуляры и объективы микроскопа делаются сменными, благодаря чему можно быстро менять увеличение системы. Быстрая смена объективов с разным увеличением осуществляется с помощью револьвера 10. Тубус и столик укреплены на массивном штативе 11.

Микроскоп как оптическое устройство включает в себя кроме оптической части ещё и часть механическую. К механической подсистеме относятся приспособления, предназначенные для закрепления исследуемого объекта и для его перемещения в различных направлениях относительно тубуса микроскопа; предметный столик с препаратоводителем и винты грубой наводки (кремальера) и тонкой наводки (микрометрический), а также штатив и тубусодержатель. К оптической системе относятся, прежде всего, объектив и окуляр, позволяющие увеличить угол зрения, под которым производится наблюдение, и устройство для освещения объекта (зеркало и конденсор) и регулирования освещения (ирисовая диафрагма).

На рис. 1.2 представлена схема хода лучей в микроскопе.

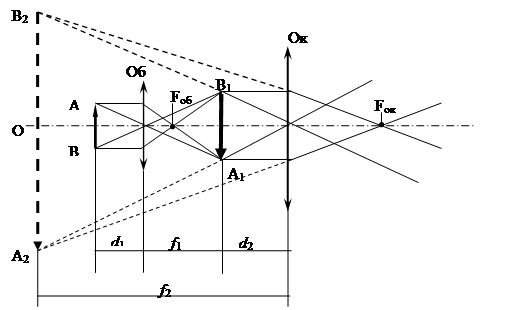Рис. 1.2. Схема хода лучей в микроскопе

Объектив (Об) создаёт действительное, увеличенное изображение А₁В₁ рассматриваемого объекта АВ. Изображение, даваемое объективом, затем рассматривается через окуляр (Ок), действующий как лупа; А₂В₂-мнимое, увеличенное изображение, полученное с помощью окуляра.

Для получения достаточно большого увеличения с помощью микроскопа необходимо, чтобы расстояние от объекта до объектива (до его передней главной плоскости) должно очень мало отличаться от его фокусного расстояния d₁ ³ F_об, как и расстояние от первичного изображения, получаемого с помощью объектива, от окуляра - от фокусного расстояния последнего. Поэтому увеличения, даваемые объективом и окуляром, можно приближённо выразить так:

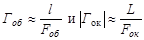, (1.1)

где – l длина тубуса микроскопа, a L - расстояние наилучшего зрения.

Более точные формулы этих увеличений имеют вид:

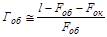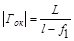и . (1.2)

Увеличение, обеспечиваемое микроскопом, равно:

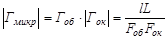. (1.3)

Из соотношения (1.3) видно, что увеличение, получаемое микроскопом, растет с уменьшением фокусного расстояния объектива и окуляра. Увеличение нельзя сделать сколь угодно большим из-за явления дифракция света, обусловленной его волновой природой. Наибольшее увеличение, получаемое с помощью оптического микроскопа, достигает 1350.

В 1873 году Аббе разработал дифракционную теорию светового микроскопа, согласно которой формирование изображения происходит благодаря двум эффектам. Сначала имеет место дифракция света на микроскопических деталях объекта, а затем, после прохождения дифрагированных световых пучков через объектив, происходит их интерференция.

С особенностями образования дифракционного изображения точечного объекта (точечного источника или рассеивателя света) связана разрешающая способность микроскопа. Когда две светящиеся точки находятся на не слишком малом расстоянии друг от друга (не меньшем длины световой волны), то при рассматривании их через микроскоп они видны раздельно. Если же эти точки сближаются, то их изображения (центральные светлые пятна, окружённые несколькими светлыми кольцами значительно меньшей интенсивности) начинают накладываться друг на друга, а затем практически сливаются в одно. Изображения двух источников (светлые пятна) можно ещё различать при условии, что центр одного из светлых пятен находится в середине первого тёмного кольца, окружающего второе светлое пятно (критерий Рэлея). Разрешающей способностью микроскопа называется величина, обратная тому наименьшему расстоянию dмежду двумя элементами структуры ("точками"), при котором они ещё могут быть видимы раздельно. Теория микроскопа приводит к формуле:

d= 1,22l/(2nsinj), (1.4)

где λ - длина волны используемого монохроматического света;

п sinj - числовая апертура объектива имеет величину, близкую к единице;

п - показатель преломления среды, находящейся между предметом и объективом;

j - угол между одним из крайних лучей, попадающих в объектив, и оптической осью объектива (см. рис.1.2).

Из формулы (1.4) видно, что улучшения (увеличения) разрешающей способности микроскопа можно добиться как за счет уменьшения длины волны l используемого света, так и увеличения числовой апертуры. Первый способ реализуется при использовании ультрафиолетового и даже рентгеновского излучений, а также электронных и ионных пучков. Второй способ основан на использовании иммерсионных жидкостей (между предметом и объективом) с показателями преломления от 1,3 до 1,8.

Показатель преломления

В электродинамике Максвелла установлено, что скорость распространения электромагнитных волн (в том числе и световых) в веществе определяется его диэлектрической и магнитной проницаемостями:

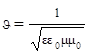. (1.5)

Для вакуума e= m= 1 и скорость распространения света в нём равна

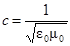. (1.6)

Из формул (1.5) и (1.6) видно, что в любом прозрачном веществе скорость света меньше, чем в вакууме в 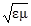раз. Значит, абсолютный показатель преломления вещества

n = 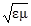. (1.7)

Поскольку для всех неферромагнетиков (каковыми являются все прозрачные вещества) m = 1, то 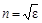. При прохождении света через границу раздела двух прозрачных сред с абсолютными показателями преломления n₁ и n₂ падающий луч АО (рис.1.3) разделяется на два луча: ОВ - отражённый луч и ОС - луч преломлённый. Оба эти луча лежат в той плоскости, в которой находятся луч падающий и нормаль к границе раздела сред в точке падения луча АО. Кроме этого, угол падения равен углу отражения, a = b, а при изменении угла падения a угол преломления g также изменяется, но так, что отношение синуса угла падения к синусу угла преломления остаётся постоянным для данных двух сред.

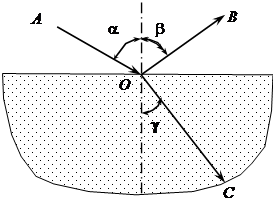Рис. 1.3. Графическое изображение отражения и преломления луча

Это отношение называется относительным показателем преломления

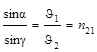. (1.8)

Из формулы (1.8) с учетом (1.7) следует, что n₂₁ = n₂ /n₁ или

n₁sina= n₂sing (1.9)

Если первой средой является воздух, для которого абсолютный показатель преломления очень близок к единице (n = 1,0003) , то для системы "воздух-вторая среда" закон преломления можно записать:

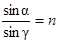, (1.10)

где п -абсолютный показатель преломления второй среды.

Известно несколько способов измерения показателей преломления твёрдых и жидких прозрачных веществ и газов. В одном из них для определения показателя преломления твёрдого вещества используется микроскоп. Этот способ основан на том, что рассматриваемый предмет через достаточно толстый слой прозрачного вещества, (твёрдого или жидкого) с плоскими параллельными поверхностями, кажется расположенным по отношению к нам ближе, чем есть на самом деле. Объясняется это следующим образом. Пусть мы смотрим на некоторую "точку" О через плоскопараллельную пластинку (рис.1.4); эта "точка" может быть, например, маленькой царапиной на нижней поверхности пластинки. От "точки" лучи идут по разным направлениям (рассеиваются).

	В

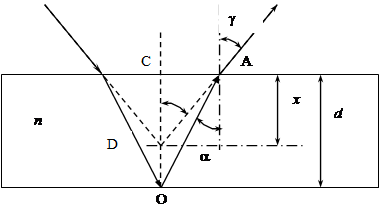Рис.1.4. Ход луча в тонкой пластинке

Возьмём луч ОА, идущий в стекле и выходящий в воздух в точке А; в этом случае угол преломления больше угла падения. Если луч АВ попадает в глаз, то мы видим изображение "точки" О в положении D; нам кажется, что "точка" О находится на расстоянии х от верхней грани пластинки, заметно меньшем её толщины d. Опираясь на правило обратимости лучей в геометрической оптике, можно записать закон преломления в виде:

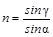. (1.11)

Из треугольников ОАС и ДАС получим:

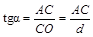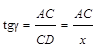, . (1.12)

При малости углов aи gтангенсы этих углов можно заменить синусами, погрешности при этом оказываются весьма малыми, если же заменить отношение синусов малых углов отношением их тангенсов, то погрешность вообще оказывается ничтожно малой. При такой замене получается

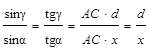. (1.13)

Сопоставляя выражения (1.11) и (1.13), получаем:

n= d/x.(1.14)

Отсюда видно, что для определения показателя преломления стекла (или иного прозрачного материала) надо измерить действительную и кажущуюся толщину пластинки и затем взять их отношение.

Порядок выполнения работы

1. Измерьте (не менее трёх раз) микрометром (штангенциркулем) толщину пластинки.

2. С помощью зеркала, находящегося под предметным столиком микроскопа, и конденсора направьте пучок света от осветителя так, чтобы поле зрения микроскопа было освещено хорошо и одинаково, но не слишком ярко.

3. Поместите исследуемую пластинку на предметный столик так, чтобы под центром объектива оказалось перекрестие продольной и поперечной рисок. Путем перемещения тубуса микроскопа или предметного столика при иной конструкции с микроскопа добейтесь хорошей видимости сначала одной, а потом другой риски в средней части поля зрения, при этом можно слегка смещать саму пластинку.

4. Поворачивая головку микрометрического винта, опустите тубус микроскопа в крайнее нижнее положение и затем поставите головку на "нуль". С помощью винта наводки (кремальеры) получите чёткое изображение риски, находящейся на нижней стороне пластинки.

5. Вращая микрометрический винт и считая число оборотов, поднимите тубус так, чтобы стала отчётливо видна риска, находящаяся на верхней стороне пластинки. Кажущаяся толщина пластинки будет равна

x = (0,1N + 0,002m) мм, (1.15)

где N - число оборотов головки микрометрического винта;

m - число делений на головке винта, характеризующее её последний неполный оборот;

0,1 и 0,002 - числа, показывающие (в мм) величину перемещения тубуса микроскопа (относительно предметного столика) при одном полном обороте головки микрометрического винта и при её повороте на одно деление.

6. Измерения провести не менее 5 раз (вообще нечётное число раз). Результаты измерений и расчётов занесите в таблицу.

Таблица

№ п/п	d, мм	dср	Отсчет по головке	x, мм	n	ncp	Dn	Dncp	e%
N	m

Показатель преломления: n = n ± Dn =

Вопросы для допуска к работе

1. Сформулируйте задачи и цель работы.

2. Как измерить истинную толщину исследуемой пластинки? Какова цена деления используемого микрометра или штангенциркуля?

3. Назначение и устройство микроскопа.

4. Как найти кажущуюся толщину пластинки?

5. Что выражает формула: x= (0,1N +0,002m) мм? Поясните смысл символов N и т, атакже коэффициентов 0, 1 и 0, 002?

6. Как определяется абсолютная и относительная погрешность измерения показателя преломления?

7. Как вычисляется показатель преломления пластинки в данной работе?

Контрольные вопросы

1. Сформулируйте законы геометрической оптики.

2. Каков физический смысл абсолютного и относительного показателей преломления?

3. Вывести используемую при расчёте формулу показателя преломления.

4. Из каких основных элементов состоит микроскоп?

5. Изобразить схему хода лучей в микроскопе.

6. Как определить увеличение, даваемое микроскопом?

7. Что понимается под разрешающей способностью оптического прибора и от чего она зависит?

8. Вывести закон преломления света на основе принципа Гюйгенса.

9. Рассчитать скорость света в использованном в работе веществе.

Литература

1. Ландсберг Г. С. Оптика. - М.: Наука, 1976, гл. 1, §1, 2; гл. 14, § 92.

2. Савельев И. В. Курс общей физики. Т.2. - М.: Наука, 1978. С.314-319, С.324-328, С.335-336.

3. Яворский Б. М., Пинский А. А. Основы физики.- М.: Высш. шк., 1981, т. 2, гл. 65, §§1, 2.

4. Сивухин Д. В. Общий курс физики. т. 4. - М.:Наука, 1980, т. 4, гл. 1, гл. 2, гл. 5, §64, 65.

5. Матвеев А. Н. Оптика. - М.: Высш. шк., 1985, гл. 4, § 25.

6. Трофимова Т. Н. Курс физики. - М.: Высш. шк., 1990. с.261-267.

Лабораторная работа № 2

Определение радиуса кривизны поверхности линзы

путем измерения колец Hьютона

Цель работы: изучение явления интерференции света на примере колец Ньютона

Приборы и принадлежности: прибор для наблюдения колец Ньютона; лазер гелий-неоновый с блоком питания; микрообъектив с увеличением 20^x или 40^x; оптическая скамья; экран; линейка с миллиметровыми делениями.

Краткая теория

Согласно классической электродинамике, свет представляет собой электромагнитные волны, т. е. взаимно связанные и взаимно обусловленные колебания электрического и магнитного полей, распространяющиеся в среде с определенной конечной скоростью u. Векторы напряженности электрическогоЕ и магнитного Н поля перпендикулярны друг другу и направлению распространения электромагнитной волны, поэтому электромагнитные волны поперечны. При изучении электромагнитных волн можно ограничиваться рассмотрением колебаний лишь вектора Е, т.к. действие света на вещество (в том числе и на элементы сетчатки нашего глаза) в основном определяется электрическим полем электромагнитной волны (в силу этого вектор Еназывается световым).

Интерференция света относится к ряду явлений, в которых обнаруживается волновая природа света. Интерференцией волн называется такое наложение друг на друга систем волн, в результате которого в пространстве образуются устойчивые области усиленных и ослабленных колебаний. Условием интерференции волн, в том числе и световых, является, во-первых, одинаковое направление колебаний в них и, во-вторых, их когерентность (согласование), т.е. одинаковость частот (периодов) колебаний источников волн. Последнее означает сохранение разности фаз колебаний, приходящих в любую точку среды, по крайней мере, в течение времени, достаточного для регистрации результата интерференции. Источники, испускающие волны одинаковой длины, также называются когерентными.

Пусть когерентные источники световых волн располагаются в точках S₁и S₂(рис.2.1), находящихся на расстоянии d друг от друга. Точка М находится на экране Э на расстояниях r₁и r₂ от источников. Ось X лежит на экране, а начало координат располагается прямо против середины отрезка d. Выясним, при каком условии в точке М наблюдается максимум освещенности (т.е. максимум интенсивности результирующих световых колебаний)или, напротив, минимум освещенности.

Уравнения волн, пришедших от источников S₁ и S₂ в точку М, имеют вид:

E₁= E₀₁cos(wt– kr₁) и E₂= E₀₂cos(wt– kr₂). (2.1)

Здесь E₀₁и E₀₂ - амплитуды колебаний напряженности электрического поля в волнах, приходящих от обоих источников в точку М экрана; k = 2p/l - модуль волнового вектора.

Примем для упрощения расчетов, что эти амплитуды равны между собой (E₀₁ =E₀₂ = E₀).

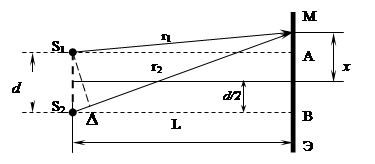Рис. 2.1.Интерференция от 2-х источников света

Вывод условий максимума и минимума опирается на принцип суперпозиции: результат нескольких одновременных воздействий представляет собой геометрическую и алгебраическую сумму результатов, вызываемых каждым воздействием в отдельности. Суперпозиция колебаний или волн - геометрическое сложение смещений и скоростей колеблющейся точки в обоих колебательных движениях (волнах) или геометрическое сложение векторов, например, E₁и E₂ колеблющихся полей. Поскольку интерференция света имеет место при одинаковости направлений векторов E₁ и E₂, то геометрическое сложение можно заменить алгебраическим.

Уравнение результирующего колебания получается при сложении обоих уравнений (2.1) в виде:

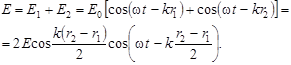
Амплитуда результирующего колебания равна

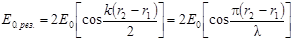. (2.3)

Обозначив разность хода волн r₂ –r₁ = D, получим

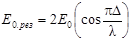. (2.4)

Т.к. интенсивность колебаний равна

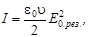
где I = wu- среднее значение плотности энергии электромагнитной волны, u - скорость волны;

,

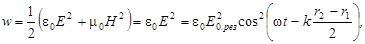
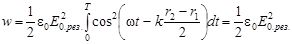то

I = 2e₀uE₀²cos²(pD/l) или I = e₀uE₀² (1 + cos(pD/l). (2.5)

Из последнего выражения видно, что максимум интенсивности имеет место при условии:

cos(pD/l) = 1, т.е. при 2pD/l=2pm, (2.6)

где m = 0; +1; +2 и т.п., или при D = ml.

Как следует из (2.6) для максимальной освещенности в точке М экрана в разности хода волн должно укладываться целое число волн или четное число полуволн.

С другой стороны, минимум интенсивности обнаруживается при

cos(2pD/l) = -1, т.е. 2pD/l = p(2m +1)

и, значит при

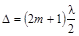, (2.7)

т.е. в разности хода волн должно укладываться нечетное число полуволн.

Для получения в лабораторных условиях двух когерентных систем волн надо разделить испускаемые источником света волны на две системы (затем они "сводятся" в одной области пространства, называемой интерференционным полем), причем так, чтобы была обеспечена и пространственная и временная когерентность получаемых и "сводимых" затем волн. Временная когерентность характеризует способность световых волн, возникающих в одной "точке" (малой области поверхности) источника в разные моменты времени, все еще интерферировать между собой. Пространственная же когерентность характеризует способность к интерференции волн, исходящих из разных "точек" источника одновременно.

Существуют два способа получения интерферирующих световых пучков из одного исходного пучка. Первый способ основан на делении волнового фронта; осуществляется он с помощью щелей Юнга, бизеркала и бипризмы Френеля, билинзы Бийе и др. Этот способ применим только в случае очень малых источников света, когда сравнительно легко обеспечивается пространственная когерентность по всему сечению светового пучка. При другом способе пучок делится на одну или несколько частично отражающих и частично пропускающих свет поверхностей; этот способ - способ деления амплитуды - может использоваться при наличии протяженных источников света; он позволяет получить интерференционную картину со значительно большей яркостью по сравнению с той, которую обеспечивает первый способ.

Определим положение максимумов при интерференции света по методу Юнга. Схема расчета представлена на рис. 2.1. Здесь L -расстояние от плоскости, в которой располагаются "вторичные" источники света S₁ и S₂, до экрана, d - расстояние между источниками, х - расстояние от нулевого максимума до максимума m-го порядка (точка М), а ∆ - разность хода волн. Из треугольника S₂MB имеем

(S₂M)² =L² + (x +d/2)²,

а из треугольника S₁MB –

(S₁M)² =L² + (x - d/2)².

Вычитая из первого равенства второе, получаем

(S₂M)² - (S₁M)² = 2xd.

Это соотношение, выражая через радиус-векторы и учитывая, что при L >> d: r₂ @ r₁ @ L, а r₂ – r₁ = D, можно представить в следующем виде

(S₂M)² - (S₁M)² = r₂² –r₁² = (r₂ –r₁)( r₂ +r₁) @ 2LD.

Откуда следует, что 2LD = 2xd, и

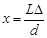(2.8)

Для максимума m-го порядка D = ml , поэтому

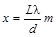(2.9)

Если когерентные световые пучки проходят пути r₁ и r₂ в разных средах с абсолютными показателями преломления п₁и п₂, скорости распространения света в этих средах соответственно равны u₁ =с/n₁ и u₂ =с/n₂, то время прохождения светом расстояний r₁ и r₂ будет одинаковым (а расстояния - таутохронными), если r₁/u₁ = r₂/u₂, или r₁n₁/с = r₂n₂/с, т.е. при r₁n₁ = r₂n₂.

Величина, выражаемая произведением геометрической длины пути на абсолютный показатель преломления среды, называется оптической длиной пути (l_опт = rn). Если r₁n₁ = r₂n₂, то пути r₁ и r₂ будут оптически эквивалентными, т.к. они не вносят дополнительной разности фаз, их оптические длины равны между собой l_опт1 = l_опт2. При равенстве оптических длин путей световых волн (лучей) соответствующие пути называются таутохронными, или равновременными. При прохождении когерентными световыми пучками разных сред условие интерференционного максимума следующее

D_опт = l_опт2 - l_опт1 = r₂n₂ – r₁n₁= ml = 2m(l/2), (2.10)

а условие минимума

D_опт = (2m + 1)(l/2) (2.11)

Т.к. как векторы E и Нобразуют правовинтовую систему (рис.2.2), то ясно, что при отражении электромагнитных (т.е. и световых) волн должно происходить наряду с изменением направления вектора uтакже изменения направления одного из векторов E или Нна противоположное. Если e₂ >e₁ (n₂ > n₁), т.е. вторая среда является оптически более плотной, то при отражении света происходит изменение направления вектора E (светового вектора), т.е. фаза колебаний электрического поля изменяется на Dj = p, а вектор H при этом не изменяет своего направления. Изменение фазы на πпри отражении от оптически более плотной среды эквивалентно условному изменению пути волны на ее полдлины. Кажущееся изменение оптической длины при этом отражении называют "потерей полдлины волны". Поэтому это можно учесть, добавив к разности хода волн (или вычтя из нее) половину длины волны в вакууме, т. е. D¢ = D ± l /2.

Важным случаем интерференции света является интерференция, происходящая вследствие отражения светового пучка на передней и задней поверхностях тонкой прозрачной пленки (вообще тонкого слоя вещества) (рис.2.3). В точке А луч разделяется на 2 луча: отраженный в точке А от верхней поверхности пленки и луч, входящий внутрь пленки и отраженный в т. В от нижней поверхности. Интерференция в отраженном свете наблюдается при наложении лучей 1 и 2. CD -волновой фронт.

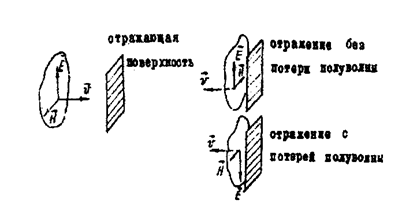
Рис. 2.2. Расположение векторов E, Hи u в падающей и отражённой

волнах

Оптическая разность хода

D¢ = (АВ +BС) n – AD = 2hn/cosg - 2htggsina = 2hncosg.

С учетом отражения волны в т. А от более плотной среды условие максимума в этом случае следующее

2hncosg + l/2 = ml или 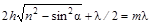, (2.12)

а условие минимума

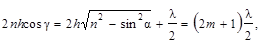(2.13)

где т = 1, 2, 3, …

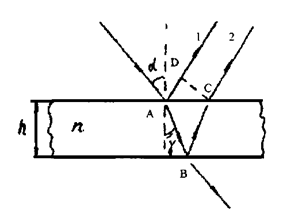
Рис. 2.3. Интерференция в тонкой плёнке

Если на плоскую стеклянную пластину положить выпуклую линзу, то между ними образуется тонкий слой воздуха, толщина которого постепенно увеличивается по всем направлениям от точки соприкосновения. Осветив пластинку и линзу монохроматическим светом, можно увидеть как в отраженном, так и в проходящем (но менее контрастно) свете интерференционную картину - чередующиеся светлые и темные кольца, называемые кольцами Ньютона. Для случая нормального (или почти нормального) падения света на линзу формулы (2.12) и (2.13) преобразуются в следующие соотношения

2h +l/2 = ml и 2h = m¢l (m =1; 2; 3 .. и m¢ = 0; 1; 2 ..). (2.14)

Здесь учтено, что g = 0 и cosg = 1, а для воздуха п = 1, 0003.

Вцентре колец Ньютона, приняв нужные меры, можно наблюдать темное пятно, которому соответствует порядковый номер m' = 0; темным же кольцам соответствуют, как и кольцам светлым, номера 1, 2, 3, 4 и т. д.

Рассчитаем радиусы темных колец Ньютона, наблюдаемых в отраженном свете. Пусть в точке А линза своей нижней поверхностью соприкасается с пластинкой, в точке В наблюдается минимум m-го порядка (рис. 2.4), через нее проходит т-oетемное кольцо радиуса r_m. Тогда на основании теоремы Пифагора можно записать:

.

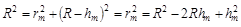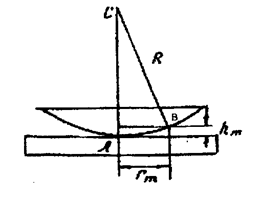
Рис. 2.4. Установка для наблюдения колец Ньютона.

Т.к. толщина слоя воздуха в месте наблюдения т-го темного кольца во много раз меньше радиуса кольца r_т и тем более радиуса кривизны линзы, то членом h_m в последнем выражении можно пренебречь, и тогда .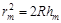

Учитывая второе соотношение из (2.13) 2h_m = ml, получаем

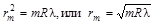. (2.16)

Для светлых колец, наблюдаемых в отраженном свете, можно записать следующее выражение:

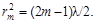(2.17)

Из формулы (2.16) можно получить выражения для определения радиуса кривизны нижней поверхности линзы или длины волны используемого монохроматического света:

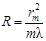, (2.18)

или

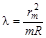. (2.19)

Формула (2.18) непосредственно не может быть использована для определения радиуса кривизны поверхности линз; при ее выводе предполагалось, что линза в одной точке (точнее, на очень малой площади) плотно прилегает к стеклянной пластинке. В действительности же из-за наличия пылинок и т. п. на стеклянной пластинке или линзе между ними образуется даже в месте их наибольшего сближения не учитываемый воздушный зазор толщиной d. Вследствие этого возникает дополнительная разность хода интерферирующих световых волн в 2d. Условие образования темных колец принимает вид:

2h_m + 2d = ml,

откуда можно получить

2h_m = ml - 2d. (2.20)

Подставляя выражение (2.20) в формулу (2.15), получаем для т-готемного кольца

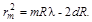(2.21)

Поскольку из равенства (2.21) нельзя определить R, то надо составить аналогичное равенство для другого, например, i-го темного кольца:

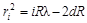(2.22)

Из соотношений (2.21) и (2.22) исключаем не измеряемую в опыте величину d и получаем:

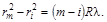(2. 23)

В результате получим формулу для расчета радиуса кривизны:

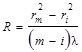. (2.24)

Порядок выполнения работы

ВНИМАНИЕ!Работая с лазером, соблюдайте предельную осторожность. Попадание в глаза прямого или отраженного от гладкой металлической поверхности пучка лазерного света опасно для зрения. С лазером обращайтесь очень осторожно. Даже легкие толчки могут вывести его из строя. Длина волны излучения гелий-неонового лазера - 632,8 нм.

1. Придвиньте к выходному отверстию (или к зеркалу, поворачивающему лазерный пучок) работающего лазера микрообъектив. Проверьте правильность установки объектива: ось расходящегося (конического) пучка света должна располагаться вдоль оптической скамьи.

2. На пути расходящегося светового пучка расположите диафрагму с прибором для наблюдения колец Ньютона так, чтобы передняя поверхность линзы оказалась в области пучка целиком. Предварительно измерьте диаметр линзы (ее оправы).

3. Рядом с лазером и с оптической скамьей (или лучше, на самой скамье около микрообъектива; при этом свет из него проходит через отверстие в экране) расположите к нему листок бумаги (лучше - миллиметровой). Поворачивая диафрагму, получите изображение колец Ньютона на экране.

4. Измерьте диаметр светлого кружка на экране. Сравнив его с диаметром оправы линзы, определите линейное поперечное увеличение k. Результаты измерений занесите в таблицу № 1.

5. Измерьте на экране диаметры двух темных колец Ньютона (например, 5-го и 10-го). Если есть возможность, определите диаметры еще двух темных колец. Можно отметить на листе, прикрепленном на экране, положения противоположных точек выбранных колец, а затем снять этот лист и провести измерения.

6. Расчеты проводите по формуле (2.24), учтя, что действительные диаметры колец Ньютона в k раз меньше измеренных на экране. Результаты измерений и вычислений занесите в таблицу № 2.

7. Определите относительную и абсолютную погрешности измерения.

Таблица № 1

Диаметр оправы прибора, мм	Диаметр светлого круга на экране, мм	Линейное увеличение изображения, k

Таблица №2

№ кольца	Диаметр кольца на экране, D	Диаметр действительного кольца, D	Радиус кольца Ньютона, r	Радиус кривизны поверхности линзы, R0

Результат вычислений: R = R₀ ± DR =

Контрольные вопросы к работе

1. Что такое интерференция света?

2. Назовите условия получения и наблюдения интерференции света.

3. Какие Вам известны способы получения двух когерентных световых пучков из одного?

4. Запишите условия интерференционного максимума и минимума.

5. Поясните результат интерференции при отражении в тонком слое вещества.

6. Объясните образование колец Ньютона.

7. Что называется оптической длиной пути?

8. Выведите формулы радиусов темных и светлых колец Ньютона в отраженном свете.

9. Как и почему изменяется вид колец Ньютона, если их наблюдать в проходящем свете?

Литература

1. Савельев И. В. Курс общей физики. Т. 2. – М.: Высш. шк, 1978. гл. XVII, §119, §122.

2. Г. С. Ландсберг Г. С. Оптика, гл. 4, § 12, § 13, § 16; гл. 6, § 25, § 26, § 27.

3. Д. В. Сивухин Д. В. Общий курс физики. Оптика. – М.:Высш. шк, гл. 3, § 26, § 27, § 33.

4. Детлаф А. А., Яворский Б. М. Курс общей физики. – М.:Высш. шк., 2002. гл. 31.

Лабораторная работа № 3

Определение ширины дифракционной щели, периода дифракционной решетки и длины световой волны

Цель работы: ознакомление с действием на свет прозрачной дифракционной щели, дифракционной решетки, определение ее периода, а также длины световой волны.

Приборы и материалы: лазер гелий-неоновый с блоком питания, оптическая скамья, диафрагма с раздвижной щелью, диафрагма (держатель) с дифракционной решеткой, объектив, осветитель с лампой накаливания, две линейки с сантиметровыми и миллиметровыми делениями.

Краткая теория

Дифракция света проявляется в отклонении световых волн от прямолинейного распространения при прохождении света через малые отверстия или мимо краев непрозрачных тел (частиц), находящихся в оптически однородной среде. Дифракцию света можно наблюдать, если размеры препятствий или отверстий одного порядка с длиной световых волн или тогда, когда место наблюдения дифракции находится на большом расстоянии от препятствий или отверстий.

В основе понимания дифракционных явлений лежит принцип Гюйгенса - Френеля: каждая точка волновой поверхности может рассматриваться в качестве источника вторичных элементарных волн, амплитуды и фазы которых одинаковы для всех точек этой поверхности. Проведя огибающую всех вторичных волн, можно найти новое положение фронта волны (рис. 3.1).

Рис. 3.1. Образование волновых поверхностей по Гюйгенсу

Это новое положение волновой поверхности является результатом интерференции вторичных волн, возникших в более ранний (предшествующий) момент времени. Колебания в любой точке среды есть результат наложения волн, пришедших в нее от множества вторичных источников, и представляют собой интерференционный эффект. При распространении световых волн свет наблюдается только там, где вторичные волны при интерференции не гасят друг друга.

Рассмотрение многих дифракционных явлений облегчается при использовании понятия зон Френеля. Пусть в некоторый момент времени волновой фронт, создаваемый источником света S, имеет форму сферы CC₁ (рис.3.2). Все точки волнового фронта являются когерентными источниками вторичных волн. Световые колебания в точке Р, находящиеся на расстоянии r₀ от фронта волны, являются результатом интерференции всех элементарных волн, приходящих в Р от отдельных элементов волнового фронта. По методу Френеля вокруг точки Р проводят ряд сферических поверхностей радиусами r₀, r₀ +l/2, r₀ +2l/2, r₀ +3l/2, и т.д., которые вырезают на волновом фронте одну центральную зону в виде поверхности шарового сегмента и множество кольцевых зон. Полученные таким образом участки волновой поверхности и называют зонами Френеля. Так как расстояния от соседних зон