Квантовая природа излучения. Тепловое излучение и его характеристики. Закон Кирхгофа. Законы Стефана-Больцмана и Вина.
Первый закон Кирхгофа. Излучение электромагнитных волн (свечение тел) может осуществляться за счет различных видов энергии. Самым распространенным является тепловое излучение, т.е. испускание электромагнитных волн за счет внутренней энергии тел. Все остальные виды свечения, возбуждаемые за счет любого вида энергии, кроме внутренней (тепловой), объединяются под общим названием люминесценция.
Тепловое излучение имеет место при любой температуре, однако, при невысоких температурах излучаются практически лишь длинные (инфракрасные) электромагнитные волны.
Рассмотрим замкнутую полость, стенки которой имеют температуру T (в ней могут находиться другие тела). Благодаря излучению стенок полость заполнена электромагнитным излучением со всевозможными направлениями распространения, поляризациями и частотами. В равновесном состоянии во всех точках полости устанавливается одинаковая и неизменная плотность энергии излучения 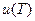 , зависящая от температуры T. Более того, стационарность равновесного состояния подразумевает, что в каждой точке полости устанавливается одинаковое распределение энергии по спектру и изотропная направленность излучения, в том числе каждой спектральной составляющей. Это позволяет ввести спектральную плотность энергии
, зависящая от температуры T. Более того, стационарность равновесного состояния подразумевает, что в каждой точке полости устанавливается одинаковое распределение энергии по спектру и изотропная направленность излучения, в том числе каждой спектральной составляющей. Это позволяет ввести спектральную плотность энергии 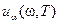 , так что произведение
, так что произведение 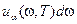 дает долю плотности энергии, приходящейся на интервал частот dw. Очевидно, между
дает долю плотности энергии, приходящейся на интервал частот dw. Очевидно, между 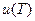 и
и 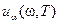 существует следующая связь
существует следующая связь
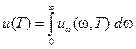 . (18-1)
. (18-1)
Внутренняя энергия излучения связана с объемной плотностью соотношением
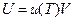 . (18-2)
. (18-2)
Легко установить, что спектральная (и объемная) плотность энергии не зависит от свойств стенок полости и представляет собой универсальную функцию частоты и температуры (объемная плотность – только температуры). Данное утверждение составляет содержание первого закона Кирхгофа.
Действительно, пусть две такие полости с разными материалами стенок, но одинаковой температурой имеют хотя бы для одной частоты w разные спектральные плотности. Тогда соединяя их с помощью отверстия (возможно со встроенным светофильтром), мы получили бы сначала поток энергии от одной полости к другой при равенстве температур, а затем от полости с более низкой температурой к полости с более высокой температурой, что запрещено принципами термодинамики.
Второй закон Кирхгофа. Поток энергии, испускаемой единицей поверхности излучающего тела по всем направлениям (в пределах телесного угла 2p), называют энергетической светимостью тела 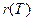 , которая зависит от температуры. Излучение состоит из волн различных частот w. Обозначим через
, которая зависит от температуры. Излучение состоит из волн различных частот w. Обозначим через 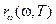 спектральную плотность энергетической светимости (испускательная способность) тела, так что произведение
спектральную плотность энергетической светимости (испускательная способность) тела, так что произведение 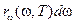 дает долю излучаемой энергии, приходящейся на интервал частот dw. Очевидно, между
дает долю излучаемой энергии, приходящейся на интервал частот dw. Очевидно, между 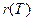 и
и 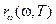 существует связь следующего вида
существует связь следующего вида
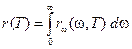 . (18-3)
. (18-3)
Пусть на элементарную площадку поверхности тела падает поток лучистой энергии 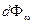 , приходящийся на интервал частот dw. Часть этого потока
, приходящийся на интервал частот dw. Часть этого потока 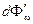 будет поглощена телом. Безразмерная величина
будет поглощена телом. Безразмерная величина
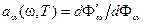 (18-4)
(18-4)
называется поглощательной способностью тела ( 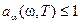 ). Тело, полностью поглощающее упавшее на него излучение всех частот (
). Тело, полностью поглощающее упавшее на него излучение всех частот ( 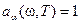 ) называется абсолютно черным. Тело, для которого
) называется абсолютно черным. Тело, для которого 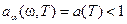 , называют серым.
, называют серым.
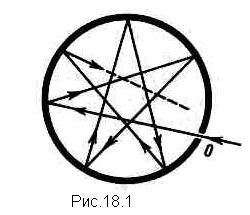
Абсолютно черных тел не существует. Сажа, например, имеет поглощательную способность 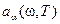 , близкую к единице, лишь в очень ограниченном интервале частот; в далекой инфракрасной области ее поглощательная способность заметно меньше единице. Реализовать абсолютно черное тело можно в виде полости с небольшим отверстием (рис.18.1). Лучи попадающие через отверстие внутрь полости, в результате многократных отражений на внутренних стенках полости практически полностью поглощаются и не выходят наружу. Это обстоятельство наглядно проявляется, например, при взгляде на открытые окна в доме, которые в светлый день кажутся темными. Высокие поглощающие свойства сажи отчасти объясняются ее пористостью, благодаря чему падающий свет испытывает перед последним отражением несколько промежуточных. Излучение, исходящее из отверстия, в свою очередь, может рассматриваться как излучение абсолютно черного тела.
, близкую к единице, лишь в очень ограниченном интервале частот; в далекой инфракрасной области ее поглощательная способность заметно меньше единице. Реализовать абсолютно черное тело можно в виде полости с небольшим отверстием (рис.18.1). Лучи попадающие через отверстие внутрь полости, в результате многократных отражений на внутренних стенках полости практически полностью поглощаются и не выходят наружу. Это обстоятельство наглядно проявляется, например, при взгляде на открытые окна в доме, которые в светлый день кажутся темными. Высокие поглощающие свойства сажи отчасти объясняются ее пористостью, благодаря чему падающий свет испытывает перед последним отражением несколько промежуточных. Излучение, исходящее из отверстия, в свою очередь, может рассматриваться как излучение абсолютно черного тела.
Обозначим через 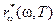 испускательную способность абсолютно черного тела. Согласно второму закону Кирхгофа между испускательной и поглощательной способностью любого тела существует связь
испускательную способность абсолютно черного тела. Согласно второму закону Кирхгофа между испускательной и поглощательной способностью любого тела существует связь
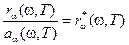 . (18-5)
. (18-5)
Обосновать закон можно исходя из энергетического баланса на поверхности тела между падающим, отраженным и испущенным излучением. Этот баланс должен выполняться не только в целом, но и в каждом спектральном интервале.
Вследствие изотропии излучения, из каждой точки полости исходит поток энергии, равномерно распределенный и равный в расчете на единицу телесного угла 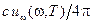 . На единицу площади поверхности полости за единицу времени под углом q к нормали в телесном угле
. На единицу площади поверхности полости за единицу времени под углом q к нормали в телесном угле 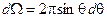 падает поток энергии
падает поток энергии 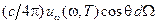 . Общее количество падающей энергии в единичном интервале частот равно
. Общее количество падающей энергии в единичном интервале частот равно
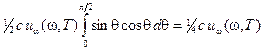 .
.
В результате отражения падающего излучения и собственного излучения в полость с единичной поверхности тела идет поток энергии
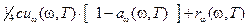 .
.
Так как тепловое равновесие не должно нарушаться, то между энергией падающего и идущего от поверхности излучения должно выполняться равенство. На этом основании приходим ко второму закону Кирхгофа (5) с установлением связи
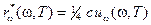 . (18-6)
. (18-6)
Закон Стефана-Больцмана. Электромагнитным излучением переносится импульс. Если объемная плотность энергии плоской волны равна u, то объемная плотность импульса 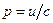 . По этой причине равновесное излучение оказывает давление на стенки полости. Нетрудно установить (подсчитав импульс падающего и уходящего от стенки излучения), что это давление не зависит от материала стенки и равно одной трети плотности энергии излучения
. По этой причине равновесное излучение оказывает давление на стенки полости. Нетрудно установить (подсчитав импульс падающего и уходящего от стенки излучения), что это давление не зависит от материала стенки и равно одной трети плотности энергии излучения
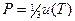 . (18-7)
. (18-7)
Используя термодинамическое соотношение
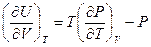
и выражения (18-2) и (18-7), приходим к уравнению
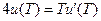 .
.
Интегрируя, получаем отсюда для объемной плотности энергии формулу
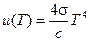 , (18-8)
, (18-8)
а для энергетической светимости абсолютно черного тела выражение
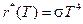 . (18-9)
. (18-9)
Соотношение (18-9) носит название закона Стефана-Больцмана, а константа s – постоянной Стефана-Больцмана.
Закон смещения Вина. Вин теоретически обосновал второй закон черного излучения из общего характера функции 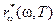 . Он рассмотрел процесс адиабатического сжатия излучения, заключенного внутри идеально зеркального сосуда. Принимая во внимание изменение частоты излучения при отражении от движущегося зеркала (эффект Доплера), Вин пришел к выводу, что испускательная способность черного тела имеет вид
. Он рассмотрел процесс адиабатического сжатия излучения, заключенного внутри идеально зеркального сосуда. Принимая во внимание изменение частоты излучения при отражении от движущегося зеркала (эффект Доплера), Вин пришел к выводу, что испускательная способность черного тела имеет вид
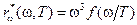 . (18-10а)
. (18-10а)
Испускательная способностью 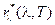 , выраженная в шкале длин волн, связана с
, выраженная в шкале длин волн, связана с 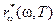 , выраженной в шкале частот, формулой
, выраженной в шкале частот, формулой
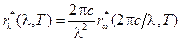
(ее легко установить из соотношений 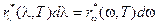 и
и 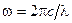 ). Используя формулу (18-10а), находим общий вид функции
). Используя формулу (18-10а), находим общий вид функции 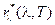
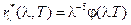 . (18-10б)
. (18-10б)
Соотношение (18-10б) позволяет установить зависимость между длиной волны 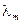 , на которую приходится максимум функции
, на которую приходится максимум функции 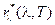 , и температурой. Представим (18-10б) в виде
, и температурой. Представим (18-10б) в виде 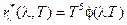 . Из него с очевидностью вытекают два закона. Согласно первому – закону смещения Вина
. Из него с очевидностью вытекают два закона. Согласно первому – закону смещения Вина
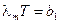 , (18-11)
, (18-11)
где 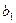 – постоянная Вина. Согласно второму закону Вина максимум испускательной способности абсолютно черного тела возрастает пропорционально пятой степени абсолютной температуры
– постоянная Вина. Согласно второму закону Вина максимум испускательной способности абсолютно черного тела возрастает пропорционально пятой степени абсолютной температуры
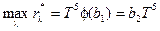 . (18-12)
. (18-12)
Закон смещения Вина объясняет, почему при нагревании тел они светятся сначала красным светом, переходя затем к белому калению.
Формула Рэлея-Джинса. С точки зрения электромагнитной теории равновесное излучение в полости представляет собой систему стоячих волн с разными частотами w, направлениями распространения и поляризациями. Найдем число различных стоячих волн в единице объема с частотами в интервале от w до w+dw. Допустим для простоты, что полость представляет собой куб с ребрами длины l, ориентированными вдоль координатных осей (результат, очевидно, не должен зависеть от формы полости).
Уравнение стоячей волны имеет вид
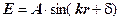 , (18-13)
, (18-13)
где E электрическое поле (аналогичное уравнение имеет место и для магнитного поля), k представляет собой волновой вектор, направление которого совпадает с направлением волны, а модуль равен 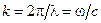 , d – начальная фаза, и A – амплитуда волны. Для поля должны выполняться периодические граничные условия. Физически это связано с тем, что в зависимости отражающих свойств стенок на них должны находиться либо узлы, либо пучности стоячих волн. Отсюда получаются условия
, d – начальная фаза, и A – амплитуда волны. Для поля должны выполняться периодические граничные условия. Физически это связано с тем, что в зависимости отражающих свойств стенок на них должны находиться либо узлы, либо пучности стоячих волн. Отсюда получаются условия
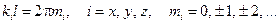 . (18-14)
. (18-14)
Частоты волн принимают, следовательно, квантованные значения
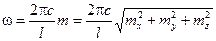 .
.
Введем пространство чисел 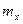 ,
, 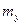 ,
, 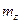 . Каждой частоте соответствует в этом пространстве точка. На каждую точку приходится куб, с объемом равным единице. Число точек в сферическом слое с радиусом m и толщиной dm равно с большой точностью объему этого слоя
. Каждой частоте соответствует в этом пространстве точка. На каждую точку приходится куб, с объемом равным единице. Число точек в сферическом слое с радиусом m и толщиной dm равно с большой точностью объему этого слоя 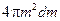 . Учитывая две независимые поляризации (на каждую точку приходится две волны), находим отсюда число стоячих волн
. Учитывая две независимые поляризации (на каждую точку приходится две волны), находим отсюда число стоячих волн 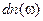 в интервале частот от w до w+dw
в интервале частот от w до w+dw
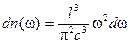 .
.
Согласно закону равнораспределения энергии по степеням свободы каждая колебательная степень свободы в состоянии равновесия имеет энергию kT. Половина из которой приходится на электрическую, другая на магнитную составляющую энергии волны. В результате получим
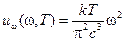 . (18-15)
. (18-15)
Равенство (18-15) называется формулой Рэлея-Джинса. Она дает достаточно хорошее согласие с экспериментом при малых w. При больших w спектральная плотность значительно превосходит наблюдаемую. Полная объемная плотность излучения, согласно формулам (18-1) и (18-15), имеет бесконечно большое значение 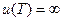 . Этот недопустимый результат (равновесная величина
. Этот недопустимый результат (равновесная величина 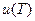 имеет конечное значение) получил название ультрафиолетовой катастрофы.
имеет конечное значение) получил название ультрафиолетовой катастрофы.
Формула Планка. С классической точки зрения вывод формулы Рэлея-Джинса является безупречным. В связи с этим возникла необходимость изменения некоторых положений классической теории.
В 1900 г. Планк предположил, что электромагнитное излучение испускается в виде отдельных порций, величина которых пропорциональна частоте излучения
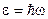 . (18-16)
. (18-16)
Коэффициент пропорциональности 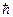 получил впоследствии название постоянной Планка. Если излучение испускается порциями
получил впоследствии название постоянной Планка. Если излучение испускается порциями 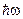 , то его энергия будет кратна этой величине
, то его энергия будет кратна этой величине
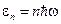 ,
,
где n – целое неотрицательное число.
В состоянии равновесия распределение энергии стоячей волны (моды колебаний) должно подчиняться распределению Больцмана. Вероятность того, что энергия моды колебаний имеет значение 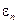 , определяется выражением
, определяется выражением
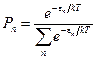 .
.
Тогда средняя энергия данной моды найдется как
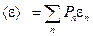 .
.
Проведя суммирование, получим
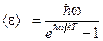 . (18-17)
. (18-17)
Заменив в (18-15) kT на полученное выражение áeñ, приходим к формуле Планка
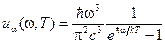 . (18-18)
. (18-18)
Формула Планка точно согласуется с экспериментальными данными во всем интервале частот и дает исчерпывающее описание равновесного излучения.
