Законы Ома и Джоуля–Ленца по классической теории
Заряд 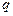 , помещенный в электрическое поле напряженностью
, помещенный в электрическое поле напряженностью 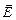 , испытывает действие силы
, испытывает действие силы 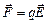 и приобретает ускорение
и приобретает ускорение 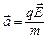 , т.е. движение не является равномерным. При столкновении с ионами электроны теряют скорость, и затем под действием сил поля вновь ускоряются до
, т.е. движение не является равномерным. При столкновении с ионами электроны теряют скорость, и затем под действием сил поля вновь ускоряются до 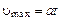 , где
, где 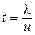 – время свободного пробега между соударениями,
– время свободного пробега между соударениями, 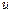 – скорость хаотического движения,
– скорость хаотического движения, 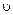 – скорость движения электронов
– скорость движения электронов 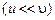 ,
, 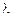 – длина свободного пробега между соударениями.
– длина свободного пробега между соударениями.
Отсюда 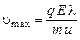 , тогда средняя скорость
, тогда средняя скорость 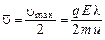 . С учетом этого выражение для плотности тока:
. С учетом этого выражение для плотности тока:
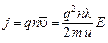 ,
,
где 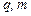 – заряд и масса электрона;
– заряд и масса электрона; 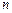 – число электронов в единице объема;
– число электронов в единице объема; 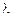 – длина свободного пробега;
– длина свободного пробега; 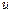 – скорость хаотического движения электронов.
– скорость хаотического движения электронов.
Если обозначить 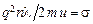 , то выражение для плотности тока примет вид:
, то выражение для плотности тока примет вид: 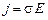 . Это соотношение совпадает с экспериментальным законом Ома в дифференциальной форме.
. Это соотношение совпадает с экспериментальным законом Ома в дифференциальной форме.
Выведем закон Джоуля–Ленца на основе классической теории. Энергия, приобретенная электроном в поле напряженностью 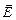 за время между двумя столкновениями с ионами кристаллической решетки равна:
за время между двумя столкновениями с ионами кристаллической решетки равна: 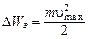 , где
, где 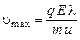 – скорость электрона перед столкновением с узлом кристаллической решетки, как это было показано выше при выводе закона Ома.
– скорость электрона перед столкновением с узлом кристаллической решетки, как это было показано выше при выводе закона Ома.
Отсюда: 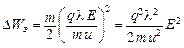 . За секунду электрон испытывает
. За секунду электрон испытывает 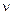 столкновений:
столкновений: 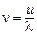 . Энергия, сообщаемая одним электроном ионной решетке за одну секунду, равна:
. Энергия, сообщаемая одним электроном ионной решетке за одну секунду, равна:
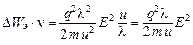 .
.
В единице объема содержится 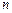 свободных электронов, за одну секунду они сообщат ионной решетке энергию:
свободных электронов, за одну секунду они сообщат ионной решетке энергию:
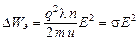 .
.
Эта формула, полученная на основе классической электронной теории, аналогична экспериментальному закону Джоуля–Ленца в дифференциальной форме.
Эффект Холла
Эффектом Холла называют возникновение поперечного электрического поля в проводнике или полупроводнике с током при помещении его в магнитное поле.
Рассмотрим проводник в форме прямоугольной пластинки (рис. 5.1), по которой течет ток плотностью j. Поместим эту пластинку с током в однородное магнитное поле так, чтобы вектор магнитной индукции был направлен перпендикулярно току.
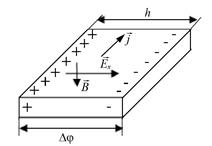 |
Под действием силы Лоренца заряженные частицы разных знаков будут скапливаться на боковых гранях проводника, образуя встречное поле, напряженностью 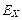 , которое действует на заряды в противоположном направлении силе Лоренца.
, которое действует на заряды в противоположном направлении силе Лоренца.
При динамическом равновесии сила, действующая на заряд внутри проводника со стороны электрического поля напряженностью 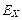 , должна уравновешиваться силой Лоренца, действующей на этот заряд со стороны магнитного поля:
, должна уравновешиваться силой Лоренца, действующей на этот заряд со стороны магнитного поля:
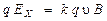 ,
,
где 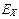 ‑ напряженность внутреннего поля, или напряженность поля Холла;
‑ напряженность внутреннего поля, или напряженность поля Холла; 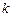 ‑ коэффициент, учитывающий конкретный проводник.
‑ коэффициент, учитывающий конкретный проводник.
Следовательно, на боковых гранях проводника возникнет разность потенциалов: 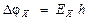 , где
, где 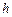 ‑ ширина проводящей пластинки.
‑ ширина проводящей пластинки.
Используя выражение для плотности тока в проводнике, выражение для скорости упорядоченного движения носителей тока в проводнике: 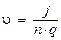 .
.
Тогда холловская разность потенциалов:
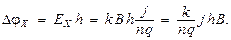
Знак разности потенциалов зависит от знака носителей заряда. Следовательно, с помощью эффекта Холла можно определять знак носителей заряда в том или ином проводнике, полупроводнике. Кроме того, по величине разности потенциалов можно определять индукцию магнитного поля, в которое внесена пластинка, что используется в различного рода приборах для измерения индукции ‑ магнитометрах.
Эффект Холла широко используется в электрооборудовании автомобилей в качестве бесконтактного датчика зажигания.
Дополнительная литература
1. Савельев И.В. Курс общей физики / И.В. Савельев. – СПб.: Лань, 2006. – Т.2. – 150 с.; Т.3. – 150 с.
2. Трофимова Т.И. Курс физики / Т.И. Трофимова. – М.: Высш. шк., 2004. – 580 с.
3. Огурцов А.Н. Лекции по физике [Электронный ресурс] /
А.Н. Огурцов. – 2004. – В 8 ч. Ч.4. Режим доступа: http://kart/edu.ua/books/ln/index.html
Оглавление
Предисловие………………………………………………………………………….. 1. Магнитное поле в вакууме……………………………………………………… 1.1. Магнитное взаимодействие токов…………………………………… 1.2.Магнитное поле. Основные свойства. Вектор магнитной индукции…………………………………………… 1.3. Силовые линии магнитного поля……………………………………. 1.4. Закон Био–Савара–Лапласа…………………………………………. 1.5. Закон Ампера………………………………………………………………… 1.6. Взаимодействие параллельных токов…………………………….. 1.7. Магнитное поле свободно движущегося заряда……………… 1.8. Сила Лоренца………………………………………………………………… 1.9. Движение заряженных частиц в магнитном поле……………. 1.10. Магнитный поток…………………………………………………………. 1.11. Работа, совершаемая при перемещении………………………. проводника с током в магнитном поле…………………………. 1.12. Основные законы магнитного поля………………………………. 1.13. Применение теоремы о циркуляции вектора  ……………. 1.14. Дивергенция и ротор векторного поля……………………….. 1.15. Дивергенция вектора ……………. 1.14. Дивергенция и ротор векторного поля……………………….. 1.15. Дивергенция вектора  магнитного поля………………….. 1.16. Действие магнитного поля на контур с током…………….. магнитного поля………………….. 1.16. Действие магнитного поля на контур с током…………….. | |
2. Магнитное поле в веществе…………………………………………………… 2.1.Магнитомеханические явления……………………………………… 2.2.Намагниченность магнетика…………………………………………. 2.3.Теоремы о циркуляции векторов 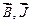 и и 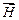 ................... 2.4.Виды магнетиков………………………………………………………….. 2.5.Условия на границе раздела двух магнетиков……………….. ................... 2.4.Виды магнетиков………………………………………………………….. 2.5.Условия на границе раздела двух магнетиков……………….. | |
| 3. Электромагнитная индукция………………………………………………….. 3.1. Явление электромагнитной индукции. ЭДС индукции. Правило Ленца……………………………………………………………… | |
| 3.2. Вихревые токи (токи Фуко)…………………………………………… 3.3. Индуктивность. Индуктивность соленоида. Явление самоиндукции. ЭДС самоиндукции…………………… 3.4. Токи при размыкании и замыкании цепи……………………….. 3.5. Энергия магнитного поля. Плотность энергии………………. | |
| 4. Уравнения Максвелла……………………………………………………………. 4.1.Основные теоремы электростатики и магнитостатики……. 4.2.Вихревое электрическое поле. Первое уравнение Максвелла……………………………………………………………………… 4.3.Ток смещения. Взаимопревращаемость электрических и магнитных полей. Второе уравнение Максвелла………….. 4.4.Третье уравнение Максвелла…………………………………………. 4.5. Четвертое уравнение Максвелла……………………………………. 4.6.Полная система уравнений Максвелла……………………………. 4.7.Общая характеристика теории Максвелла………………………. | |
| 5. Классическая теория электропроводности металлов (классическая электронная теория)………………………………………. 5.1. Природа носителей тока в металлах……………………………… 5.2.Основные положения классической электронной теории проводимости металлов……………………………………… 5.3.Законы Ома и Джоуля–Ленца по классической теории…… 5.4. Эффект Холла………………………………………………………………. | |
| Дополнительная литература……………………………………………………… |
Учебное издание
Кунаков Виктор Стефанович
Лещёва Ольга Александровна
Мардасова Ирина Владимировна
Холодова Ольга Михайловна
ЭЛЕКТРОМАГНЕТИЗМ
Редактор Т. С. Колоскова
Компьютерная обработка И. В. Чурина
Тем. план 2011 г., поз. 15
 |
В печать 17.11. 2011
Формат 60х84/16 Бумага тип № 3. Офсет.
Объем 4,0 усл.п.л. Заказ № 607 Тираж 80 экз. Цена свободная.
 |
Издательский центр ДГТУ
Адрес университета и полиграфического предприятия:
 344000, г. Ростов-на-Дону, пл. Гагарина,1
344000, г. Ростов-на-Дону, пл. Гагарина,1
