Моделирование процесса нейтрализации сточных вод.

Процесс нейтрализации сточных вод рассмотрим на примере нейтрализации сточных вод, содержащих кислые примеси, например серную кислоту известковым молоком.

Процесс нейтрализации может быть описан уравнением реакции

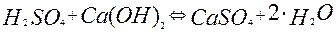(1)

В сточных водах содержится s % весовых кислых примесей в пересчете на серную кислоту. Для нейтрализации используем известковое молоко с концентрацией m % весовых. Поток кислых примесей составляет v_s м³/с с плотностью r_s кг/м³. Тогда мольный поток подлежащих нейтрализации кислых примесей составит величину

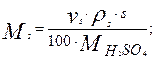(2)

Для нейтрализации этого количества кислых стоков необходим равный мольный поток известкового молока:

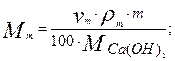(3)

Приравнивая уравнения (2) и (3) и разрешая полученное равенство относительно v_m, получим необходимый расход известкового молока:

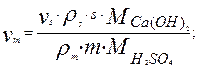(4)

Общий объемный поток в реактор будет составлять

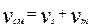(5)

Общая плотность смеси по правилу аддитивности будет равна

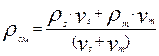(6)

Необходимый объем реактора будет равен:

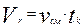(7)

Концентрации кислых примесей и известкового молока при входе в реактор при входе в реактор составят:

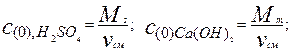(8)

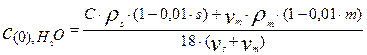(9)

Таким образом, получены все исходные формулы необходимые для расчета процесса нейтрализации в проточном реакторе идеального перемешивания

Определить необходимые условия для проведения процесса нейтрализации для потока v_s=10m³/час, начальная концентрация серной кислоты s=3%; начальная концентрация известкового молока m=10%; плотность кислых сточных вод r_s=1050 кг/м³; плотность известкового молока r_m=1100 r_s= 1100 кг/м³

Рассчитать мольные потоки и концентрации компонентов на входе в аппарат и создать модель процесса в Cascade Wizard. Для этого входим в Cascade Wizard, выбираем команду Load и из списка моделей выбираем команду 3cstrl

Появляется окно

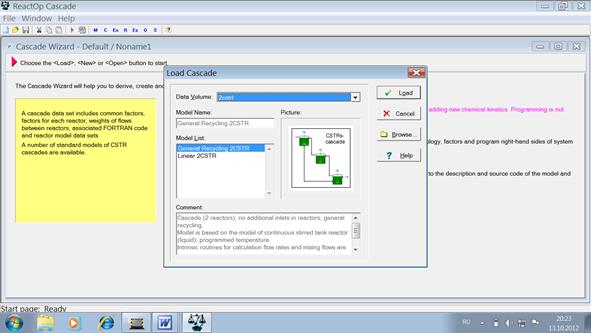
В окне выбираем модель linear 3cstr. Нажимам команду Load и попадаем в окно ввода реакций. Вводим реакцию нейтрализации:

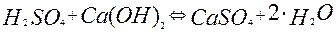
После вводим кинетические параметры реакции:

Lnk0=15; E=30 kJ/mol

Lnk0e=80: Ee=70 kJ/mol

n(H2SO4)=1

n(Ca()H)2)=1

n(CaSO4)=1

n(H2O)=2

И нажимаем команду Next, затем команду Save as

После сохранения модели, переходим в Simulation Wizard и выполняем команду New.

Из списка моделей выбираем вновь созданную модель и нажимаем команду Next.

Открывается окно созданной схемы процесса:

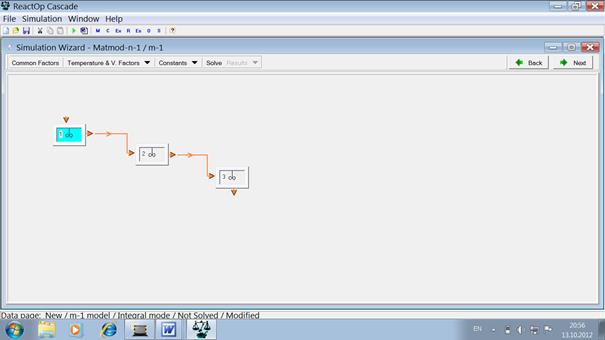
Открываем окно Common Factors и вводим данные о составе и свойствах общего потока: Fresh feed=0.2027

Ca(OH)2=0.263

CaSO4=0

H2O=56.3

H2SO4=0.263

Затем открываем окно температур и вводим температуру в 1-м реакторе – 300 К. Затем открываем окно Constants и вводим начальный состав в реакторе (все нули) и состав входного потока, рассчитанный ранее.

Ca(OH)2=0.263

CaSO4=0

H2O=56.3

H2SO4=0.263

Volumetric Low Rate=0.2027m3/min

Reactor Volume=2 m3

Затем проделываем те же операции для остальных реакторов каскада. Только для остальных реакторов каскада вводим только значения Volumetric Low Rate=0.2027m3/min и Reactor Volume=2 m3, так как остальные входные значения принимаются равными выходным из предыдущего реактора, которые рассчитываются при решении задачи моделирования каскада.

После ввода всех исходных данных, нажимаем команду Solve и получаем решение системы уравнений модели.

Отмечаем и записываем концентрацию серной кислоты на выходе из последнего аппарата каскада.

Затем переходим к 1-му аппарату каскада, вводим значение объема для 1-го аппарата каскада 6м³ и нажимаем команду Solve. Получаем решение, соответствующее проведению всего процесса нейтрализации в одном аппарате объемом 6м³. Отмечаем и запоминаем полученный результат. Затем устанавливаем объемы 1-го и 2-го аппарата по 3 м³. Запоминаем результат. Строим в Excell график зависимости конечной концентрации от числа аппаратов в каскаде и делаем вывод о влиянии секционирования на эффективность процесса. Оформляем отчет с изложением цели моделирования, процедуры построения модели, результатов моделирования и выводов об эффективности секционирования.

Литература

1. Ю.В.Шариков, И.Н. Белоглазов, А.Ю. Фирсов Моделирование процессов и объектов в металлургии, СПбГГИ, Санкт-Петербург, 2006

2. Ю.В.Шариков, И.Н. Белоглазов, Моделирование систем. Часть I. Санкт-Петербург, 2011

3. Ю.В.Шариков, И.Н. Белоглазов, Моделирование систем. Часть II. Санкт-Петербург, 2012