Измерение ускорения свободного падения с помощью математического и физического маятников

Оглавление

Лабораторная работа № 1 _________________________ 3

Измерение ускорения свободного падения с помощью математического и физического маятников

Лабораторная работа № 2_________________________ 9

Измерение скорости тела методом баллистического маятника

Лабораторная работа № 3_________________________15

Соударение шаров

Лабораторная работа № 4_________________________22

Проверка теоремы Гюйгенса - Штейнера методом вращательных колебаний

Лабораторная работа № 5_________________________30

Маятник Обербека

Лабораторная работа № 6_________________________37

Колебания пружинного маятника

Лабораторная работа № 7_________________________42

Определение коэффициента трения скольжения

Лабораторная работа № 8_________________________52

Маятник Максвелла

Лабораторная работа № 9_________________________61

Изучение механического резонанса

Лабораторная работа № 10_________________________71

Изучение кинематики и динамики поступательного движения на машине Атвуда

Лабораторная работа № 11_________________________81

Изучение колебаний связанных маятников

Лабораторная работа № 12_________________________92

Определение скорости звука

Лабораторная работа № 13_________________________103

Определение теплопроводности воздуха

Лабораторная работа № 14_________________________109

Измерение отношения Cp/Cv воздуха

Лабораторная работа № 15_________________________119

Изучение изобарного процесса

Лабораторная работа № 16_________________________124

Изучение изотермического процесса

Лабораторная работа № 17_________________________130

Изучение изохорного процесса

Лабораторная работа № 18_________________________134

Определение коэффициента поверхностного натяжения жидкости методом отрыва петли

Лабораторная работа № 1

Измерение ускорения свободного падения с помощью математического и физического маятников

Цель лабораторной работы

Целью лабораторной работы является изучение процессов и параметров свободных колебаний и параметров математического и физического маятников.

Задачи лабораторной работы

Задача лабораторной работы состоит в определении ускорения свободного падения с помощью математического и физического маятников.

3. Экспериментальное оборудование, приборы и

Принадлежности

Рис.1

Лабораторный стенд (рис.1) с физической моделью математического маятника в виде металлического шарика (1), физический (оборотный) маятник (2), оптоэлектрический датчик.

К приборам и принадлежностям относятся также компьютер с необходимым программным обеспечением, соединительный кабель для подключения оптоэлектрического датчика к компьютеру, измерительная линейка.

Теоретическая часть

Периоды колебаний математического и физического маятников зависят от величины ускорения свободного падения g. Период колебаний Т математического маятника равен:

(1)

где l- длина нити математического маятника, точнее, расстояние от точки подвеса до центра шарика. В случае физического маятника

(2)

где m - масса физического маятника, l - расстояние от оси вращения до его центра масс, J - момент инерции физического маятника относительно оси вращения.

Таким образом, для определения g с помощью математического маятника достаточно измерить его период колебаний Т и длину l, после чего рассчитать ускорение свободного падения g по формуле:

(3)

которая следует из (1).

Проводить измерения g с помощью произвольного физического маятника, опираясь на формулу (2), достаточно затруднительно, т. к. при этом необходимо знать точное значение его момента инерции, положение центра масс и массу. Однако существует прибор, называемый оборотным маятником, при использовании которого задача определения ускорения свободного падения сводится к измерению периода колебаний и некоторого расстояния между элементами конструкции оборотного маятника.

Оборотный маятник является физическим маятником, который устроен следующим образом (см. рис. 2). На стержне (1) закрепляются два груза (2, 3). Стержень имеет две оси вращения (4, 5), расположенные по обе стороны от центра масс системы. Оси вращения для уменьшения трения выполняют в виде

треугольных призм из твердого материала, которые следует устанавливать на специальную опору, закрепленную на подставке.

Оборотный маятник регулируется таким образом, чтобы период его колебаний при установке на одной призме равнялся периоду колебаний его на другой призме. Регулировка производится путем изменения взаимного расположения грузов и призм на стержне.

Выведем формулу периода колебаний оборотного маятника. Согласно формуле Гюйгенса - Штейнера, момент инерции J маятника относительно произвольной оси вращения равен:

(3)

где J_c — момент инерции относительно оси вращения, проходящей через центр масс, m — масса маятника, а l— расстояние от оси вращения до центра масс. После подстановки (4) в (2) формула для периода колебаний физического маятника примет вид:

Поскольку оборотный маятник имеет равные периоды колебаний на обеих призмах (осях), полученное соотношение используем для двух расположений маятника:

(5)

Здесь l₁ и l ₂ — расстояния от центра масс маятника до ребра первой и второй призмы соответственно.

Возведем формулы (5) в квадрат и умножим на знаменатели правых частей:

Вычтем из первого равенства второе и сократим на m:

Применим формулу разности квадратов в правой части:

(6)

Если в (6) l₁≠l₂, что означает несимметричность расположения призм относительно центра масс маятника, то, сокращая на (l₁- l₂), получаем:

(7)

Поскольку призмы расположены по разные стороны от центра масс, то l₁+l₂= l₀, где l₀ - расстояние между соответствующими ребрами призм (осями колебаний), или приведенная длина оборотного маятника.

На основании (7) легко записывается выражение для периода колебаний оборотного маятника:

и формула для определения g:

(8)

Еще раз подчеркнем, что в случае l₁= l₂ (симметричное расположение осей колебаний относительно центра масс маятника), формулы (8) и (9) не являются справедливыми. Величина периода колебаний в этом случае зависит не только от l₀ и g, но и от момента инерции маятника.

Цель лабораторной работы

Цель данной работы

заключается в изучении законов
сохранения количества движения и
полной механической энергии и их
применении при решении

практических задач.

Задачи лабораторной работы

Задачей работы является определение скорости шарика с помощью баллистического маятника.

Теоретическая часть

Вывод расчетной формулы основан на использовании законов сохранения полной механической энергии и сохранения момента импульса при неупругом ударе.

Ударом называется конечное изменение скоростей тел за весьма малый промежуток времени, происходящее при их столкновении.

В процессе деформации тел при ударе возникают мгновенные (ударные) силы, величина которых весьма значительна. Для системы соударяющихся тел эти силы являются внутренними. Их импульсы за время продолжительности удара называются мгновенными импульсами. Они во много раз больше импульсов за то же время всех внешних сил, приложенных к системе. Поэтому в процессе удара влиянием внешних сил можно пренебречь и считать, что система соударяющихся тел является замкнутой, т.е. з ней выполняется законы сохранения импульса (количества движения системы) и момента импульса.

Существуют два предельных вида удара: абсолютно упругий и абсолютно неупругий. Абсолютно упругимназывается такой удар, при котором механическая энергия тел не переходит в другие, немеханические, вилы энергии. При таком ударе кинетическая энергия переходит полностью или частично в потенциальную энергию упругой деформации. Затем тела возвращаются к первоначальной форме, отталкивая друг друга. В итоге потенциальная энергия упругой деформации снова переходит в кинетическую энергию, причем тела разлетаются со скоростями, величина и направление которых определяются двумя условиями - сохранением полной энергии и сохранением полного импульса системы тел и момента полного импульса.

Абсолютно неупругийудар характеризуется тем, что потенциальной энергии деформации не возникает, кинетическая энергия тел полностью или частично превращается во внутреннюю энергию и после удара столкнувшиеся тела либо движутся с одинаковой скоростью, либо покоятся. При абсолютно неупругом ударе выполняется лишь законы сохранения импульса и момента импульса, закон же сохранения механической энергии не соблюдается - имеет место закон сохранения суммарной энергии различных видов, механической и внутренней.

В момент попадания в неподвижный цилиндр баллистического маятника с конусом-уловителем шарик испытывает неупругий удар. После удара маятник с шариком начнет двигаться.

До момента попадания шарика в уловитель на систему не действуют никакие силы в горизонтальном направлении (в пренебрежении сопротивлением воздуха). Следовательно, момент импульса системы относительно оси вращения маятника остается постоянным.

(1)

где т и M - массы шарика и уловителя; v и и - скорости шарика до столкновения и шарика вместе с уловителем после столкновения; l - длина

маятника; J_cm- момент инерции стержня 4 (рис.2), связывающего корпус уловителя с осью вращения маятника. Считая в первом приближении, что длина стержня равна расстоянию от оси до середины уловителя, т.е. l, воспользуемся формулой для оценки осевого момента инерции стержня относительно его торца:

(2)

Здесь т_ст - масса стержня. Угловая скорость маятника после удара определяется из кинематики вращательного движения:

(3)

С учетом (3) после подстановки (2) в (1) получим выражение для скорости v:

u (4)

Кинетическая энергия вращательного движения системы после попадания шарика в цилиндр равна

(5)

После подстановки выражений (2) и (3) получим:

(6)

При последующем отклонении маятника в соответствии с законом сохранения механической энергии кинетическая энергия его движения переходит в потенциальную энергию сил тяжести. При максимальном его отклонении баланс энергий выглядит так:

где П{(т + M)g) и П{m_cmg) - потенциальные энергии сил тяжестей шарика с уловителем и стержня. Они определяются максимальным ростом их высот относительно своих нижних положений:

Во второй формуле в (8) введены коэффициенты 1/2 для учета положения центра тяжести стержня относительно оси вращения.

Приравняв правые части (6) и (7) с учетом (8), получим выражение для скорости движения маятника после столкновения и:

Воспользовавшись (4), можно получить расчетную формулу для определения скорости шарика:

Лабораторная работа № 3

Соударение шаров.

Цель лабораторной работы

Изучение законов сохранения импульса и энергии на примере задачи о соударении шаров.

Задачи лабораторной работы

Задача данной лабораторной работы состоит в измерении времени пролета шаров мимо оптоэлектрических датчиков непосредственно перед столкновением и после него, расчете скоростей их движения и проверке законов сохранения импульса и энергии. Проверка заключается в сравнении результатов эксперимента с выводами, следующими из законов сохранения энергии и импульса.

Теоретическая часть

Совместное применение законов сохранения энергии и импульса для прямого и центрального упругого удара двух шаров позволяет получить следующие соотношения для модулей скоростей движения первого (V₁) и второго (V₂) шаров после соударения:

(1)

(2)

где m₁ m₂- массы первого и второго шаров, V₀₁, V₀₂ - модули скоростей первого и второго шаров до соударения.

В эксперименте, выполняемом в данной лабораторной работе, один из шаров первоначально покоится (V₀₂=0), поэтому формулы (1) и (2) упрощаются:

(3)

(4)

Если массы шаров одинаковы (т₁=т₂), то соотношения (3) и (4) принимают вид:

V₁=0 (5)

V₂ = V₀₁ (6)

т.е. в результате столкновения налетающий шар останавливается, а второй шар начинает движение со скоростью, равной скорости первого шара до удара.

Очевидно, что кинетическая энергия системы Т до столкновения равна (второй шар в экспериментах первоначально покоится):

(7)

а кинетическая энергия системы после взаимодействия Т вычисляется по формуле:

(8)

Экспериментальная часть данной лабораторной работы состоит в проверке на простой лабораторной установке законов сохранения импульса и энергии. Проверка заключается в проведении измерений, результаты которых обрабатываются и сравниваются количественно с выводами, следующими из законов сохранения энергии и импульса.

Лабораторная работа № 4

Цель лабораторной работы

Изучение возможности проверки теоремы Штейнера методом вращательных колебаний.

Задачи лабораторной работы

Используя результаты измерений момента инерции свободного стола и периода его колебаний методом вращательных колебаний, провести экспериментальную и теоретическую проверку теоремы Гюйгенса -Штейнера.

Принадлежности

Рис.1

Лабораторная установка (рис.1) включает колебательную систему 1, вращающуюся в горизонтальной плоскости, и устройство 2 для измерения жесткости используемых пружин.

К приборами

Принадлежностям относятся

оптический датчик 3, с помощью которого измеряется период колебаний системы, компьютер с необходимым программным обеспечением и концентратор для подключения датчика к компьютеру.

Рис.2

Колебательная система (рис.2) состоит из закрепленного на вертикальной оси шкива 1, ремень 2 которого связан с упругими пружинами 3, зацепленными за штыри стойки. К шкиву жестко прикреплен металлический профиль 4 с рядом отверстий 5, в которых фиксируются грузы 6. Вращательные колебания регистрируются оптическим датчиком 7 в форме импульсов при перекрытии оптической оси датчика язычком 8, жестко скрепленным со шкивом колебательной системы.

Теоретическая часть

Найдем связь между моментом инерции Jподвижной части колебательной системы и периодом колебаний Т. В положении равновесия силы упругости пружин, а, следовательно, и силы натяжения нити с разных сторон от стола, равны. Обозначим эти силы F₀. Для выведения шкива из положения равновесия повернем его на угол φ. Тогда натяжение одной пружины увеличится, а другой уменьшится на φd/2, где d — радиус шкива. По закону Гука силы упругости изменятся на kdφ/2, здесь k- коэффициент жесткости одной пружины. На шкив будет действовать возвращающий момент сил:

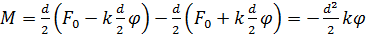(1)

Согласно основному уравнению вращательного движения

Jε= М. (2)

Подставляя (1) в (2)и учитывая, что 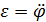, получаем

дифференциальное уравнение для φ:

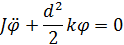
Из теории дифференциальных уравнений следует, что его решение имеет вид:

φ(t)= φ₀cos(ωt + α). Здесь φ₀ и α- константы, определяемые начальными условиями, а

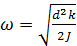(3)

- частота колебаний. Из формулы (3) видим, что момент инерции обратно пропорционален квадрату частоты:

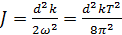(4)

Здесь учтено, что 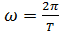Следовательно, моменты инерции

подвижной части колебательной системы относятся как квадраты частот их колебаний. Окончательно получаем, что отношение моментов инерции подвижной части колебательной системы

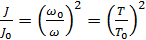(5)

Здесь нулевым индексом отмечены параметры системы, выбранной в качестве эталонной.

За эталонную примем такую подвижную систему, у которой грузы (рис.3) располагаются соосно на оси шкива - в его центральном отверстии, один над другим (в позиции "0-0").

Жесткость упругой связи к, входящую в выражение (4), можно определить по величине растяжения пружин X под действием весовой нагрузки:

G = kX, (6)

Откуда

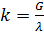(7)

Рис.3

Для определения момента инерции эталонной системы Jo применим формулу (4):

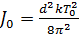(8)

Сформулируем теорему Гюйгенса- Штейнера:

Момент инерции тела относительно произвольной оси равен моменту инерции относительно параллельной ей оси, проходящей через центр масс, плюс произведение массы тела на квадрат расстояния между этими осями.

Следовательно, момент инерции подвижной системы, у которой два одинаковых груза фиксированной массы т располагаются симметрично на расстоянии гот оси шкива (рис.3, позиции "1-1", "2-2", "3-3", или "4-4") определяется выражением

J = J₀ + 2mr². (9)

Разместим на одинаковых расстояниях г от оси шкива 2 тела фиксированной массы т. После измерения периода колебаний Т производится вычисление момента инерции по формуле 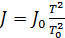(10)

(10)

где Т. и J- - период колебаний и момент инерции эталонной системы. Для проверки теоремы Штейнера по формуле (9) производится расчет момента инерции J- (его теоретическое значение) и сравнивается со значением момента инерции J_э(10), оцененного экспериментально.

Дополнительные источники

1. Приложение 1. Оценка погрешности измерений.

2. Приложение 2. Датчики, интерфейсы, программное обеспечение

Лабораторная работа № 5

Маятник Обербека

Цель лабораторной работы

Цель данной лабораторной работы состоит в экспериментальном изучении законов динамики вращательного движения твердого тела и изучении зависимости момента инерции твердого тела от распределения массы относительно неподвижной оси вращения. Момент инерции тела является мерой инертности тела при вращательном движении и аналогичен массе тела при его поступательном движении.

Задачи лабораторной работы

Задача данной лабораторной работы заключается в том, чтобы экспериментально и теоретически определить, как изменяется момент инерции вращающегося тела при изменении распределения массы относительно неподвижной оси вращения. Момент инерции тел простой геометрической формы можно вычислить по простым формулам. Знание моментов инерции элементов машин и механизмов необходимо для проведения расчетов, связанных с их вращательным движением. В этом заключается прикладное значение изучения методов определения моментов инерции.

Принадлежности

Маятник Обербека (рис.1) представляет собой крестовину 1, на вращающейся оси 3, на шкив которой намотана нить с грузиком 5 массой т₀.

Рис. 1

На четырех взаимно перпендикулярных стержнях крестовины располагаются четыре подвижных груза 2 массой т каждый. Под действием силы тяжести груза 5 нить разматывается с оси и вызывает вращательное движение крестовины. На оси крестовины располагается датчик 4 угловой скорости вращения маятника.

К приборам и принадлежностям относятся компьютер с необходимым программным обеспечением и соединительный кабель для подключения датчика угловой скорости к компьютеру.

Теоретическая часть

При изменении расстояния перемещаемых грузов от оси крестовины маятника Обербека угловое ускорение s крестовины тем меньше, чем больше момент инерции тела Jотносительно оси вращения. Определить величину углового ускорения е можно с помощью уравнения динамики вращательного движения:

Jε = M, (1)

где М— момент сил, действующих на маятник, J- момент инерции маятника. Ускорение а груза т₀ связано с угловым ускорением ε формулой

а = εd/2, (2)

где d- диаметр диска, на который намотана нить.

Вращательный момент силы М, действующий на маятник, определяется выражением:

M = Td/2-M_T, (4)

где Т— сила натяжения нити, М_Т - момент сил трения в оси.

С другой стороны, сила Т вместе с силой тяжести вызывает движение груза с ускорением а:

m₀a= m₀g-T (5)

Отсюда момент силы можно выразить так:

M = m₀(g-a)d/2-M_T (6)

Если подставить (6) в (1), воспользовавшись формулой (2), получим выражение:

Jε = m₍₎(g - εd/2) d/2 - M_T,

после преобразования которого уравнение динамики маятника Обербека приобретет вид:

(J + m₀ d²/4)ε = m₀ gd/2 - M_T (7)

Теоретическое значение момента инерции крестовины с 4-мя грузами

J = J₀+ 4J_m + 4mr². (8)

Здесь J_o - суммарный момент инерции крестовины без грузов, J_m -

момент инерции подвижного груза относительно оси, проходящей через его центр масс и параллельной оси вращения крестовины, r - расстояние от оси вращения маятника до центра масс грузов, m - масса каждого из четырех подвижных грузов.

Величина J_m+ тr²в (8) есть момент инерции подвижного груза относительно оси вращения крестовины. При этом использована теорема Гюйгенса - Штейнера:момент инерции тела относительно любой оси вращения равен моменту инерции тела относительно параллельной оси, проходящей через центр масс тела, плюс произведение массы тела на квадрат расстояния между осями.

В данной работе необходимо определить постоянную часть момента инерции маятника Обербека - величину J_c = J₀ + 4J_m, не зависящую от расположения подвижных грузов на крестовине.

Поскольку величина момента трения в оси неизвестна, воспользоваться для этого впрямую формулой (7) нельзя.

Если рассмотреть два положения грузов относительно оси маятника r₁ и r₂, то можно переписать дважды (7). С учетом (8) эти выражения приобретут вид:

Равенство правых частей этих равенств означает и равенство их левых частей:

Отсюда можно найти искомую величину J_c:

(12)

Формула (12) являются расчетной в данной работе.

Лабораторная работа № 6

Цель лабораторной работы

Целью лабораторной работы является экспериментальное изучение колебаний пружинного маятника и ознакомление с методами определения параметров механических колебаний.

Задачи лабораторной работы

Задачей лабораторной работы является измерение зависимости периода колебаний от жесткости пружин и массы грузов.

Экспериментальное

Оборудование, приборы и

Принадлежности

Лабораторный стенд (рис.1) включает в себя вертикальную опорную конструкцию с направляющими пазами 1, а также набор пружин и подвижную каретку 2, в отверстии которой может фиксироваться дополнительный груз (рис.2).

К приборам и принадлежностям относятся оптический датчик 4, компьютер с необходимым

Программным обеспечением,

концентратор для подключения датчика к компьютеру.

Рис. 1

Теоретическая часть

В линейных упругих системах действует закон Гука: (1)

где F_упр-величина упругой силы, например, пружины, измеряемая в ньютонах, k- коэффициент жесткости пружины (Н/м),

λ-растяжение/сжатие пружины (м) из положения своего недеформированного состояния.

Рассмотрим силы, действующие на пружинный маятник, расположенный вертикально (силами сопротивления движению пренебрежем). Это: сила тяжести mg и сила упругого подвеса F_ynp, стремящаяся вернуть пружину в исходное, нерастянутое положение.

Второй закон Ньютона для этого случая можно написать так:

(2)

Если отсчитывать смещение тела х из своего положения статического равновесия, в котором растяжение пружины равно статическому λ_сm, то проекция этого уравнения на наклонную плоскость (ось х) будет:

(3)

где х-ускорение тела, определяемое как вторая производная по времени от смещения х, а величина λ_сm + х - полное растяжение пружины.

Условием равновесия тела массой m на пружине является равенство силы тяжести и статической упругой силы пружины mg = F_упр^ст.В свою

очередь, равновесная статическая упругая сила пружины определяется статическим смещением из положения равновесия λ_сm. Тогда:

(4)

С использованием (4) уравнение (3) приобретет вид: что после нормировки (деления на m) позволяет его записать в виде:

(5)

Здесь

Выражение (5) - дифференциальное уравнение свободных колебаний. Решение дифференциального уравнения (5) представляет собой гармонические колебания вида:

(6)

Здесь А, φ- амплитуда и начальная фаза колебаний, а величина ω

носит название частоты собственных колебаний. По частоте колебаний определяют период колебаний Т:

(7)

Используя значение периода колебания, можно найти и жесткость пружины:

(8)

В том случае, если использовать два различных груза m₁и m₂, то по соответствующим периодам собственных колебаний оценивают жесткость пружины (динамический метод):

(9)

Лабораторная работа № 7

Цель лабораторной работы

Изучить закон сухого трения и ознакомиться с методами определения коэффициента трения скольжения.

Задачи лабораторной работы

Провести экспериментальную работу по оценке кинематических параметров равноускоренного движения тела по наклонной плоскости. На основании экспериментальных данных провести расчет коэффициента трения скольжения.

Теоретическая часть

Среди возможных сил, препятствующих движению, можно выделить одну, наиболее часто встречающуюся: силу сухого трения. Сила сухого трения представляется двумя видами: силой трения покоя, силой трения скольжения.

Сила сухого трения возникает между соприкасающимися телами и направлена по касательной к поверхности соприкосновения тел против направления движения или против силы, пытающейся вовлечь тела в движение. Необходимым условием возникновения силы сухого трения является наличие давления одного тела на поверхность другого (рис. 2 а, б,в).

Сила давления тела на опору называется весом тела. По третьему закону Ньютона ответом опоры на действие силы давления является сила

реакции опоры F реакции, которую принято представлять суммой силы нормальной реакции опоры и силы сухого трения:

F_{реакции}= N + F_тр (1)

Если соприкасающиеся тела неподвижны относительно друг друга, то возникающую силу сухого трения называют силой трения покоя, а при относительном перемещении тел - силой трения скольжения. Скольжение тел относительно друг друга начинается только после того, как внешняя касательная к поверхности соприкосновения тел сила (тангенциальная сила) превзойдет по размеру силу трения покоя. Таким образом, сила трения покоя изменяется от нуля до некоторого максимального значения и равна внешней силе (или ее проекции), действующей в противоположном направлении.

Рис.2

Сила трения зависит от силы давления, или прижимающей силы, материала тел и состояния поверхностей соприкосновения. У шероховатых поверхностей трение покоя больше, чем у отшлифованных.

Рис.3. График зависимости проекции силы трения на направление движения от скорости для полированных металлических поверхностей

Когда внешняя сила (тангенциальная сила) превысит размер максимальной силы трения покоя, начнется скольжение одного тела вдоль поверхности соприкосновения с другим телом. В этом случае сила трения будет направлена против вектора скорости. Ее числовое значение для хорошо отполированных металлических поверхностей при небольших скоростях практически не зависит от скорости и равно максимальной силе трения покоя. График зависимости силы трения от скорости имеет вид, изображенный на рис. 3.

Независимость силы трения от скорости соблюдается лишь при не очень больших скоростях, не для всех тел и не при всех качествах обработки поверхностей. Для других случаев график зависимости силы трения между твердыми поверхностями от скорости имеет вид, показанный на рис. 4.

Рис.4. График зависимости проекции силы трения на направление движения от скорости для произвольных твердых поверхностей

Возникновение сухого трения обусловлено взаимодействием молекул, атомов и электронов, находящихся в поверхностных слоях трущихся друг о друга тел, т. е. в конечном счете, электромагнитным взаимодействием.

Французские физики Г.Амонтон и Ш.Кулон опытным путем установили закон трения: сила трения скольжения F_mp пропорциональна силе нормального давления F_давл тела на опору:

(2)

где μ- коэффициент трения, зависящий от свойств соприкасающихся тел и состояния их трущихся поверхностей.

В соответствии с III законом Ньютона F_давл= -N, следовательно, расчет силы трения можно производить по формуле:

(3)

Модуль силы трения скольжения определяется:

(4)

Значение коэффициента трения скольжения μ можно получить, решив задачу о движении тела по наклонной плоскости с углом наклона α(рис. 5).

Рис.5. Схема действия сил и выбора координатных осей системы отсчета для решения задачи о соскальзывании тела с наклонной плоскости

Тело, находясь на наклонной плоскости, приходит в движение, когда проекция результирующей всех действующих на тело сил на ось х будет больше 0. В случае решения задачи со схемой действующих сил, указанной на рис. 4, движение тела начинается, когда проекция силы тяжести (mg)_xбудет больше размера силы трения F_mp. Следовательно, в случае равенства проекции силы тяжести на .х-ось (mg)_xи силы трения тело будет либо покоиться, либо двигаться с постоянной скоростью. Тогда

0=(mg)_x-F_mp (5)

или

mgsina=μN (6)

В проекции на ось у

0= - mgcosα+N (7)

При этом

N=mgcosα. (8)

Тогда подстановка значения N из (8) в уравнение (6) дает:

mg-sina—/иmg-cosa, (9)

следовательно,

μ = tga. (10)

Отсюда следует, что коэффициент трения равен тангенсу угла наклона плоскости к горизонту, при котором начинается соскальзывание тела с наклонной плоскости.

Однако установить с достаточной точностью коэффициент трения скольжения μпо экспериментальному значению предельного угла начала соскальзывания тела с наклонной плоскости довольно сложно. Поэтому в данной лабораторной работе используют метод экспериментальной оценки коэффициента трения скольжения при движении тела по наклонной плоскости с ускорением.

Рис.6

Тело, пущенное с вершины наклонной плоскости, перемещается по закону равноускоренного движения

(11)

Если на пути его движения на фиксированных расстояниях поместить оптические датчики, то времена прохождений телом соответствующих координат должны быть согласованы друг с другом в соответствии с формулой (11). Используя численный алгоритм квадратичной аппроксимации экспериментальных точек, можно найти величину ускорения а.

По значению рассчитанного ускорения, используя закон движения тела (II закон Ньютона), можно определить коэффициент трения μ. Для этого запишем II закон Ньютона для тела т (см. рис. 6):

F_mp+N + mg = ma, (12)

Выразим это уравнение в проекциях на оси х и у:

х: -F_mp+mgsinα = ma_t (13)

у:_:N-mgcosα = 0 (14)

Сила трения тогда будет

F_mp=μN = μmgcosα (15)

Подставляя F_mp в уравнения проекции на ось х (13), получим

-μ. Mgcosα+ mgsinα - та (16)

Отсюда можно записать расчетную формулу для определения коэффициента трения μ:

(17).

Анализ выражения (17) показывает, что для определения коэффициента трения необходимо знать угол наклона плоскости αи ускорение тела а<