Элементы квантовой статистики
4.53.Система, состоящая из N = 1020 трехмерных осцилляторов, находится при температуре 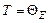 (
( 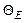 = 250 К). Определить энергию системы. [1,49 Дж].
= 250 К). Определить энергию системы. [1,49 Дж].
4.54.Используя квантовую теорию теплоемкости Эйнштейна, определить удельную теплоемкость при постоянном объеме алюминия при температуре 200 К. Характеристическую температуру Эйнштейна принять для алюминия равной 300 К. [770 Дж/кг∙К].
4.55.Определить теплоту, необходимую для нагревания кристалла калия массой 200 г от температуры T1 = 4 К до температуры T2 = 5 К. Принять характеристическую температуру Дебая для калия 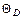 = 100 К и считать условие T <<
= 100 К и считать условие T << 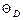 выполненным. [0,92 Дж]. 4.56.Определить в электронвольтах максимальную энергию фонона, который может возбуждаться в кристалле калия, характеризуемом температурой Дебая
выполненным. [0,92 Дж]. 4.56.Определить в электронвольтах максимальную энергию фонона, который может возбуждаться в кристалле калия, характеризуемом температурой Дебая 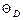 = 100 К. [0,0086 эВ].
= 100 К. [0,0086 эВ].
4.57.Оценить среднюю энергию свободных электронов в металлах при абсолютном нуле температур, если средняя концентрация электронов проводимости в металлах составляет 5∙1028 м-3. [3 эВ]. 4.58.Металлы литий и цинк приводят в соприкосновение друг с другом при температуре Т = 0 К. Чему будет равна возникшая контактная разность потенциалов? Какой из этих металлов будет иметь более высокий потенциал? ( 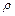 Li = 0,53∙103 кг/м3;
Li = 0,53∙103 кг/м3; 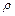 Zn = 7,15∙103 кг/м3). [U12 = 0,8 B; Li].
Zn = 7,15∙103 кг/м3). [U12 = 0,8 B; Li].
4.59.Доказать, что уровень Ферми в собственном полупроводнике действительно расположен в середине запрещенной зоны. [EF = 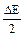 ].
].
4.60.Кремниевый образец, ширина 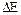 запрещенной зоны в котором равна 1,1 эВ, нагревают от температуры t1 = 0 оС до температуры t2 = 10 оС. Во сколько раз возрастает его удельная проводимость g ? [В 2,28].
запрещенной зоны в котором равна 1,1 эВ, нагревают от температуры t1 = 0 оС до температуры t2 = 10 оС. Во сколько раз возрастает его удельная проводимость g ? [В 2,28].
4.61.При нагревании германиевого кристалла от температуры 0 оС до температуры 10 оС его удельная проводимость возрастает в 1,49 раза. По приведенным данным определить ширину запрещенной зоны кристалла германия. [0,72 эВ].
4.62.Предположим, что p – n – переход находится при 0 оС и при прямом напряжении 0,1 В, a его сопротивление равно
10 Ом. Каково сопротивление перехода, если поменять полярность напряжения? [692 Ом].
4.63.Прямое напряжение, приложенное к p – n – переходу, равно 0,1 В. Во сколько раз возрастет сила тока через переход, если изменить температуру от Т1=300 К до Т2=273 К? [В 1,1 раза] .
4.64.Глубина потенциальной ямы U металла составляет
10 эВ, а максимальная энергия электрона Еmax, отсчитанная от дна ямы, равна 6 эВ. Определить уровень Ферми ЕF и работу выхода А электрона в этом металле. [ЕF = 6 эВ; А = 4 эВ].
ЭЛЕМЕНТЫ ФИЗИКИ АТОМНОГО ЯДРА
И ЭЛЕМЕНТАРНЫХ ЧАСТИЦ
Физика атомного ядра
Основные формулы и законы
· Массовое число ядра (число нуклонов в ядре)
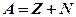 ,
,
где 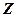 – зарядовое число (число протонов);
– зарядовое число (число протонов); 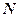 – число нейтронов.
– число нейтронов.
· Радиус ядра с массовым числом 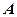
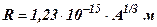 .
.
· Дефект массы ядра
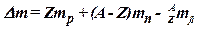 ,
,
где 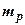 ,
, 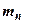 и
и 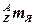 – соответственно масса протона, нейтрона и ядра.
– соответственно масса протона, нейтрона и ядра.
Если взять не массу ядра 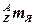 , а массу атома (изотопа)
, а массу атома (изотопа) 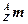 и вместо массы протона массу атома водорода
и вместо массы протона массу атома водорода 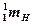 , то
, то
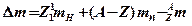 .
.
· Энергия связи и удельная энергия связи
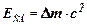 ,
, 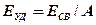 .
.
Если массы измерять в а.е.м., то 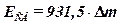 (МэВ), так как 1 а.е.м.∙с2 = 931,5 МэВ.
(МэВ), так как 1 а.е.м.∙с2 = 931,5 МэВ.
· Закон радиоактивного распада
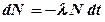 или
или 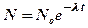 ,
,
где 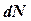 – число ядер, распадающихся за время
– число ядер, распадающихся за время 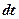 ;
; 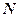 – число ядер, не распавшихся к моменту времени
– число ядер, не распавшихся к моменту времени 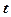 ;
; 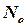 – число ядер в начальный момент времени (
– число ядер в начальный момент времени ( 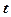 =0);
=0); 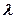 – постоянная радиоактивного распада.
– постоянная радиоактивного распада.
· Период полураспада
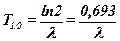 .
.
· Среднее время жизни радиоактивного ядра
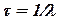 .
.
· Активность радиоактивного изотопа – число распадов за 1 с:
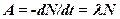 или
или 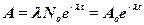 ;
;
В СИ активность измеряется в беккерелях (Бк), внесистемная единица активности – кюри (Ки), 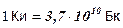 .
.
· Правила смещения для 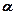 -распада
-распада
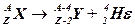 .
.
· Правила смещения для β –-распада
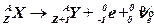 .
.
· Правила смещения для β +-распада
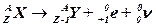 .
.
· Энергетический эффект ядерной реакции (в МэВ)
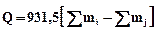 ,
,
где 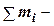 сумма масс (в а.е.м.) исходных реагентов;
сумма масс (в а.е.м.) исходных реагентов; 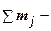 сумма масс (в а.е.м.) продуктов реакции.
сумма масс (в а.е.м.) продуктов реакции.
· Основные дозиметрические величины:
1) поглощенная доза излучения Dп = ∆Епогл/m;
2) экспозиционная доза DЭ = 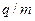 (1р = 2,58∙10-4 Кл/кг)
(1р = 2,58∙10-4 Кл/кг)
3) биологический эквивалент рентгена (1 бэр = 10-9 Дж/кг)
4) мощность дозы излучения Pп = Dп/∆t или Pэ = Dэ/∆t, где ∆t – длительность облучения.
Задания
5.1.Определить плотность частиц (нуклонов) ядерного вещества, выражаемую числом нуклонов в 1 см3, если в ядре с массовым числом А все нуклоны плотно упакованы в пределах его радиуса. Используя вычисленную плотность частиц ядерного вещества, определить плотность массы нейтронной звезды, если все нейтроны плотно упакованы в пределах всего объема звезды (mn = 1,675∙10-27 кг). [8.7∙1037 см-3; 1,46∙1017 кг/м3]
5.2.Определить энергию и удельную энергию связи для ядер изотопов 1) гелия: а) 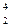 He; б)
He; б) 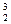 He; 2) урана: а)
He; 2) урана: а) 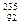 U; б)
U; б) 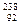 U. Какие выводы можно сделать на основе вычисленных значений энергии и удельной энергии связи? (см. примечание к п. 5.3).
U. Какие выводы можно сделать на основе вычисленных значений энергии и удельной энергии связи? (см. примечание к п. 5.3).
1) [28,4 МэВ; 7,1 МэВ/нуклон; 7,8 МэВ; 2,6 МэВ/нуклон].
2) [1786 МэВ; 7,6 МэВ/нуклон; 1804 МэВ; 7,58 МэВ/нуклон].
5.3.Определить удельную энергию связи для ядер:
1) дейтерия 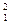 D; 2) гелия
D; 2) гелия 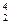 Не; 3) лития
Не; 3) лития 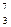 Li; 4) кислорода
Li; 4) кислорода 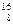 О;
О;
5) алюминия 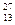 Al; 6) железа
Al; 6) железа 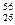 Fe; 7) ксенона
Fe; 7) ксенона 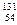 Хе; 8) золота
Хе; 8) золота 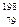 Au; 9) урана
Au; 9) урана 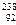 U. [1) 0,56 МэВ/нуклон; 2) 7,08 МэВ/нуклон; 3) 5,61 МэВ/нуклон; 4) 7,98 МэВ/нуклон; 5) 9,34 МэВ/нуклон; 6) 9,30 МэВ/нуклон; 7) 9,40 МэВ/нуклон; 8) 7,92 МэВ/нуклон; 9) 7,58 МэВ/нуклон].
U. [1) 0,56 МэВ/нуклон; 2) 7,08 МэВ/нуклон; 3) 5,61 МэВ/нуклон; 4) 7,98 МэВ/нуклон; 5) 9,34 МэВ/нуклон; 6) 9,30 МэВ/нуклон; 7) 9,40 МэВ/нуклон; 8) 7,92 МэВ/нуклон; 9) 7,58 МэВ/нуклон].
Примечание: для решения задач 5.2 и 5.3 используйте массы протона и нейтрона (в а.е.м.): mp = 1,00728; mn = 1,00867, а также используйте нижеприведенную таблицу.
| Изотоп | Масса (а.е.м.) | Изотоп | Масса (а.е.м.) | Изотоп | Масса (а.е.м.) |
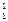 Н Н | 1,00814 | 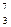 Li Li | 7,01823 | 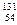 Хе Хе | 130,94662 |
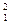 D D | 2,01474 | 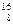 О О | 15,99491 | 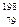 Au Au | 198,03048 |
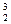 Не Не | 3,01699 | 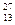 Al Al | 25,99008 | 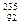 U U | 235,11750 |
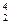 Не Не | 4,00387 | 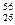 Fe Fe | 5,92264 | 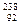 U U | 238,12522 |
5.4.Зная постоянную распада 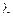 ядра, определить вероятность W того, что ядро распадается за промежуток времени от 0 до t. [ W=∆N/No=1 –
ядра, определить вероятность W того, что ядро распадается за промежуток времени от 0 до t. [ W=∆N/No=1 – 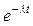 ].
].
5.5.Период полураспада некоторого радиоактивного изотопа Т1/2 = 2 с. Определить вероятность W того, что ядро не распадется на промежутке t, равном 10 с. [W = ∆N/No = 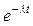 = 0,31].
= 0,31].
5.6.Определить, сколько ядер в mo = 5 мг радиоизотопа церия 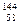 Се распадается в течение промежутков времени:
Се распадается в течение промежутков времени:
1) ∆t = 1 с; 2) ∆t = 1 год. Период полураспада радиоизотопа церия 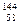 Се Т = 285 суток. [1) 6∙1011; 2) 1,25∙1019].
Се Т = 285 суток. [1) 6∙1011; 2) 1,25∙1019].
5.7.Образец содержит 1000 радиоактивных атомов (изотопов) с периодом полураспада Т1/2, Сколько атомов останется через промежуток Т/2? [250].
5.8.За какое время произойдет распад 2 мг полония 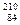 Ро, если в начальный момент его масса 0,2 мг? [28,5 мин].
Ро, если в начальный момент его масса 0,2 мг? [28,5 мин].
5.9.Сколько ядер распадается за 1 с в куске урана 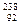 U массой 1 кг? Какая активность этого урана? [∆N = 1,236∙107 распадов/с; А = 0,33 мКи].
U массой 1 кг? Какая активность этого урана? [∆N = 1,236∙107 распадов/с; А = 0,33 мКи].
5.10.Что больше: среднее время жизни 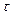 радиоактивного ядра или период полураспада Т 1/2? [
радиоактивного ядра или период полураспада Т 1/2? [ 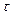 больше Т1/2 в 1,44 раза].
больше Т1/2 в 1,44 раза].
5.11.Чтобы определить возраст древней ткани, найденной в одной из египетских пирамид, была определена концентрация в ней атомов радиоуглерода 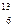 С. Она оказалась соответствующей 9,2 распадам в минуту на один грамм углерода. Концентрация
С. Она оказалась соответствующей 9,2 распадам в минуту на один грамм углерода. Концентрация 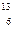 С в живых растениях соответствует 14 распадам в минуту на один грамм углерода. Период полураспада Т1/2
С в живых растениях соответствует 14 распадам в минуту на один грамм углерода. Период полураспада Т1/2 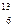 С равен 5730 лет. Исходя из этих данных, оценить возраст древней ткани. [3,5∙103 лет].
С равен 5730 лет. Исходя из этих данных, оценить возраст древней ткани. [3,5∙103 лет].
5.12.Пользуясь таблицей Менделеева и правилами смещения, определить, в какой элемент превращается радий 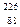 Ra после пяти
Ra после пяти 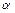 - и четырех β –-распадов. [
- и четырех β –-распадов. [ 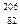 Pb].
Pb].
5.13.Определить высоту кулоновского потенциального барьера для 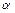 -частицы в ядре полония
-частицы в ядре полония 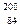 Ро. Покоившееся ядро полония испускает
Ро. Покоившееся ядро полония испускает 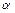 -частицу с кинетической энергией Тα= 5,77 МэВ. За счет какого эффекта
-частицу с кинетической энергией Тα= 5,77 МэВ. За счет какого эффекта 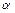 -частица вылетает из ядра? [26,6 МэВ; туннельный эффект].
-частица вылетает из ядра? [26,6 МэВ; туннельный эффект].
5.14.Используя принцип неопределенности в виде ∆r∆p≥ 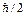 , показать, что электрон не может находиться внутри атомного ядра (
, показать, что электрон не может находиться внутри атомного ядра ( 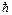 = 0,66∙10-15 эВ∙с). [∆p = 0,33 эВ∙с/м; Е = 99 МэВ ≥ 10 МэВ].
= 0,66∙10-15 эВ∙с). [∆p = 0,33 эВ∙с/м; Е = 99 МэВ ≥ 10 МэВ].
5.15.Определить энергию, выделяющуюся при следующих реакциях:
1) 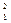 Н +
Н + 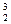 Не ®
Не ® 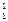 Н +
Н + 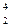 Не;
Не;
2) 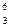 Li +
Li + 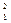 Н ®
Н ® 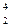 Не +
Не + 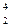 Не;
Не;
3) 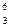 Li +
Li + 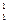 Н ®
Н ® 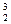 Не +
Не + 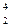 Не.
Не.
Примечание: при решении задачи используйте таблицу, приведенную к задаче 5.3; m 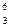 Li = 6,01703 а.е.м.
Li = 6,01703 а.е.м.
[1) 18,3 МэВ; 2) 22,4 МэВ; 3) 4,02 МэВ].
5.16.Определить наименьшую энергию g-кванта, необходимую для осуществления следующей реакции:
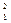 Н + g ®
Н + g ® 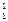 Н +
Н + 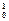
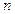 .
.
Примечание: при решении задачи используйте таблицу, приведенную к задаче 5.3.
5.17.Предположим, что для преодоления электростатического отталкивания два дейтрона 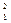 Н должны сблизиться до 10-14 м. Определить высоту электростатического потенциального барьера в МэВ. До какой температуры нужно нагреть дейтрон, чтобы преодолеть потенциальный барьер? [0,14 МэВ; 5,6∙106 К ].
Н должны сблизиться до 10-14 м. Определить высоту электростатического потенциального барьера в МэВ. До какой температуры нужно нагреть дейтрон, чтобы преодолеть потенциальный барьер? [0,14 МэВ; 5,6∙106 К ].
5.18.Ядро урана 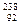 U, захватывая быстрый нейтрон, превращается в радиоактивный изотоп урана, который претерпевает
U, захватывая быстрый нейтрон, превращается в радиоактивный изотоп урана, который претерпевает 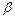 –-распад, и превращается в трансурановый элемент, который в свою очередь также претерпевает
–-распад, и превращается в трансурановый элемент, который в свою очередь также претерпевает 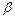 –-распад, в результате чего образуется плутоний. Записать все эти процессы в виде ядерных реакций.
–-распад, в результате чего образуется плутоний. Записать все эти процессы в виде ядерных реакций.
5.19. Определить энергию, выделяющуюся в результате реакции 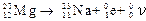 . Массы нейтральных атомов магния и натрия соответственно равны 3.8184
. Массы нейтральных атомов магния и натрия соответственно равны 3.8184 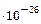 и 3,8177
и 3,8177 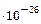 кг.
кг.
5.20.Ядро урана 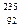 U, захватывая тепловой нейтрон, делится на изотопы стронция и ксенона с массовыми числами 95 и 139, второй из которых, являясь радиоактивным, претерпевает 3
U, захватывая тепловой нейтрон, делится на изотопы стронция и ксенона с массовыми числами 95 и 139, второй из которых, являясь радиоактивным, претерпевает 3 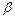 –-рас-пада. Записать реакцию деления, а также цепочку
–-рас-пада. Записать реакцию деления, а также цепочку 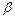 –-распадов.
–-распадов.
5.21.Французские ученые Ирэн и Фредерик Жолио-Кюри, открывшие искусственную радиоактивность, подвергли бомбардировке 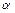 -частицами бор
-частицами бор 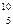 В, алюминий
В, алюминий 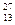 Al и магний
Al и магний 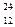 Mg. Записать соответствующие ядерные реакции. Напомним, что при данных реакциях возникают нейтроны.
Mg. Записать соответствующие ядерные реакции. Напомним, что при данных реакциях возникают нейтроны.
5.22.Сколько энергии выделится при ядерном делении 1 кг урана 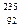 U в урановом реакторе (или в атомной бомбе)? Какое количество угля необходимо сжечь для получения такого же количества теплоты (калорийность угля принять равной 29,3 МДж/кг)? Считать, что средняя энергия, выделяющаяся при делении одного ядра урана
U в урановом реакторе (или в атомной бомбе)? Какое количество угля необходимо сжечь для получения такого же количества теплоты (калорийность угля принять равной 29,3 МДж/кг)? Считать, что средняя энергия, выделяющаяся при делении одного ядра урана 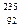 U, составляет 200 МэВ. [5,13∙1026 МэВ; 2,8∙106 кг ].
U, составляет 200 МэВ. [5,13∙1026 МэВ; 2,8∙106 кг ].
5.23.Энергия излучения Cолнца возникает вследствие цепочки термоядерных реакций, конечным результатом которых является превращение четырех ядер водорода в одно ядро гелия. Термоядерные реакции, происходящие в водородной бомбе и в предполагаемых установках по мирному использованию термоядерных реакций, в общем сводятся к тому же. Определить, какое количество воды можно было бы нагреть от 0 оС до кипения за счет превращения в гелий 4 г водорода. [ 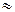 1,54∙106 кг ].
1,54∙106 кг ].
5.24.Для сравнения биологического действия различных видов излучения используется коэффициент относительной биологической активности (КОБА). Он показывает, во сколько раз действие данного излучения сильнее биологического действия 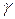 -излучения при равных видах поглощенной энергии. Ниже приведен КОБА для различных видов радиоактивных излучений. Подберите соответствующие значения КОБА для: 1) рентгеновских лучей и β-частиц; 2) a-частиц; 3) нейтронов. [1; 1–10; 10–20 соответственно].
-излучения при равных видах поглощенной энергии. Ниже приведен КОБА для различных видов радиоактивных излучений. Подберите соответствующие значения КОБА для: 1) рентгеновских лучей и β-частиц; 2) a-частиц; 3) нейтронов. [1; 1–10; 10–20 соответственно].
5.25.Какую дозу радиоактивного излучения измеряют соответствующие приборы (поглощенную или экспозиционную)?
5.26.Скорость нарастания цепной реакции задается формулой 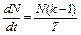 , откуда
, откуда 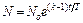 , где
, где 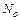 – число нейтронов в начальный момент времени;
– число нейтронов в начальный момент времени; 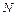 – число нейтронов в момент времени t; Т – среднее время жизни одного поколения; К – коэффициент размножения нейтронов. Определить, во сколько раз увеличится число нейтронов в цепной ядерной реакции за время t = 10 с, если среднее время жизни Т одного поколения составляет 80 мс, а коэффициент размножения нейтронов k = 1,002. [
– число нейтронов в момент времени t; Т – среднее время жизни одного поколения; К – коэффициент размножения нейтронов. Определить, во сколько раз увеличится число нейтронов в цепной ядерной реакции за время t = 10 с, если среднее время жизни Т одного поколения составляет 80 мс, а коэффициент размножения нейтронов k = 1,002. [ 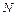 /
/ 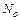 = 1,284]. 5.27.Характер зависимости
= 1,284]. 5.27.Характер зависимости 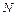 числа нейтронов в момент t цепной ядерной реакции деления тяжелых ядер, как следует из формулы, приведенной в задаче 5.26, определяется знаком выражения (k – 1). Различают: 1) развивающуюся; 2) затухающую; 3) самоподдерживающуюся реакции. Как называются режимы соответствующих цепных ядерных реакций? Какие значения k им соответствуют? [Надкритический: k >1; критический: k =1; подкритический: k <1].
числа нейтронов в момент t цепной ядерной реакции деления тяжелых ядер, как следует из формулы, приведенной в задаче 5.26, определяется знаком выражения (k – 1). Различают: 1) развивающуюся; 2) затухающую; 3) самоподдерживающуюся реакции. Как называются режимы соответствующих цепных ядерных реакций? Какие значения k им соответствуют? [Надкритический: k >1; критический: k =1; подкритический: k <1].
Физика элементарных частиц
Задания
5.28.Из приведенных ниже характеристик элементарных частиц отобрать 1) одинаковые как по величине, так и по знаку характеристики частиц и их античастиц; 2)одинаковые по величине, но противоположные по знаку характеристики частиц и их античастиц. А. [масса]. В. [электрический, барионный и лептонный заряды]. С. [спин]. D. [магнитный момент]. G. [время жизни]. E. [странность, спиральность].
5.29.Электрон и позитрон, имеющие одинаковые кинетические энергии, равные 240 кэВ, при соударении превратились в два одинаковых фотона. Определить энергию фотона и соответствующую ему длину волны. [750 кэВ; 1,65 пм].
5.30.Среди фундаментальных элементарных частиц, указанных в правой колонке таблицы, выбрать частицы, относящиеся к соответствующим классам частиц из приведенных в левой колонке.
| 1. Лептоны 2. Кварки 3. Кванты фундаментальных полей взаимодействия | А. Электрон. Б. Мюон. В. Фотон. Г. Тау-лептон. Д. Шесть типов кварков по аромату, в каждом из которых различают три цвета. Е. Электронное нейтрино. Ж. Мюонное нейтрино. З. Промежуточные векторные бозоны. И. Гравитон. К. Глюоны. Л. Тау – нейтрино. |
5.31.Из фундаментальных элементарных частиц, указанных в задании 5.30, выбрать частицы, являющиеся: 1) фермионами;
2) бозонами.
5.32.Фундаментальным физическим взаимодействиям: 1) электромагнитному, 2) гравитационному, 3) слабому, 4) сильному – подберите соответствующие кванты фундаментальных полей взаимодействия, приведенные ниже. А. [Гравитон]. B. [Глюон]. C. [W ± – частицы и Z – частицы]. D. [Фотон]].
5.33.На какие подгруппы частиц из приведенных ниже подразделяется многочисленная группа адронов, т. е. частиц, состоящих из кварков и участвующих в сильном взаимодействии? А.[Барионы]. B. [Мезоны]. C. [Гипероны (странные барионы)]. D. [Резонансы]. E. [Лептоны].
5.34.В приведенной ниже сводке законов сохранения в физике элементарных частиц выберите законы сохранения, справедливые: 1) для всех видов фундаментальных взаимодействий; 2) для электромагнитного; 3) для слабого; 4) для сильного взаимодействий.
Законы сохранения: А. Сохранение полной энергии. Б. Сохранение полного импульса. В. Сохранение полного момента импульса.
Г. Сохранение электрического заряда. Д. Сохранение барионов.
Е. Сохранение лептонов. Ж. Зарядовая независимость (или сохранение изотопического спина). З. Сохранение странности. И. Симметрия античастиц. К. Сохранение четности. Л. СР – инвариантность. М. СРТ – инвариантность. Н. Инвариантность относительно обращения времени. О. Сохранение очарования.
5.35.Радиус действия нуклон – нуклонных сил составляет примерно 1,5∙10-15 м. Какую массу должна иметь виртуальная частица, чтобы обеспечить такой радиус действия? Какие частицы являются ее реальным отображением? (при решении задачи используйте принцип неопределенности Гейзенберга в виде 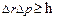 , виртуальную частицу считайте ультрарелятивистской). [m
, виртуальную частицу считайте ультрарелятивистской). [m 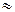 0,23∙10-27 кг ≥ 250 m e;
0,23∙10-27 кг ≥ 250 m e; 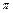 – мезоны (пионы)].
– мезоны (пионы)]. 
5.36.Нейтральный 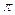 – мезон (
– мезон ( 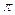 о), распадаясь, превращается в два одинаковых
о), распадаясь, превращается в два одинаковых 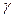 - фотона. Принимая массу пиона равной
- фотона. Принимая массу пиона равной
264 me, определить энергию каждого из возникших фотонов. Кинетической энергией и импульсом мезона пренебречь. [67,6 МэВ].
5.37.Выбрав из четырех типов нейтрино ( 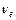 ,
, 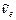 ,
, 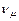 ,
, 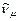 ) правильное, написать недостающие обозначения (x) в каждой из приведенных реакций и в случае бета – распада свободного нейтрона:
) правильное, написать недостающие обозначения (x) в каждой из приведенных реакций и в случае бета – распада свободного нейтрона:
1) х + 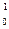 n ®
n ®  p +
p + 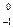 е ; 2) х +
е ; 2) х + 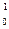 n ®
n ®  p + μ
p + μ  ;
;
3) х +  р ®
р ® 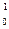 n +
n + 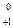 е ; 4)
е ; 4) 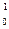 n ®
n ®  p +
p + 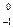 е + x.
е + x.
[ 
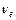 ;
; 
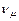 ;
; 
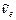 ;
; 
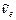 ].
].
5.38.Определить, какие из приведенных ниже процессов разрешены законом сохранения лептонного числа:
1) p → n + е 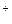 +
+ 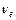 ; 2) k
; 2) k  ®
® 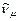 + μ
+ μ  ;
;
3) 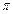
 ® μ
® μ  + e
+ e  + e
+ e  ; 4) μ
; 4) μ  ®
® 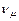 + e
+ e  +
+ 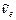 .
.
5.39.Установить, запрещены или нет перечисленные ниже реакции. Если есть запрет, то указать, с нарушением какого закона сохранения он связан.
1) 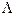
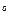 ® p +
® p + 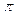
 ; 2) p +
; 2) p + 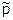 ® μ
® μ  + e
+ e  ;
;
3) n ® p + е  +
+ 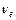 ; 4) p ® n + е
; 4) p ® n + е 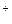 +
+ 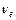 .
.
[Нарушаются законы сохранения: 1) электрического заряда; 2) мюонного и электронного лептонных чисел; 3) электронного лептонного числа; 4) энергии.]
Литература
1. Волькенштейн В.С. Сборник задач по общему курсу физики. Изд. доп. и перераб. / В.С. Волькенштейн. – СПб.: Издательство «Специальная литература»; Издательство «Лань», 1999. – 328 с.
2. Трофимова Т.И. Сборник задач по курсу физики для втузов / Т.И. Трофимова. – 3-е изд.- М.: ООО Издательский дом «ОНИКС 21 век»; ООО «Издательство «Мир и Образование»», 2003. – 384 с.
Содержание
| Общие методические указания…………………………………………………….. | ||
| 1. ИНТЕРФЕРЕНЦИЯ СВЕТА…………………………………………………………… | ||
| Основные формулы и законы………………………………………... | ||
| Задания…………………………………………………………………………. | ||
| 2. ДИФРАКЦИЯ И ПОЛЯРИЗАЦИЯ СВЕТА………………………………………. | ||
| Основные формулы и законы………………………………………... | ||
| Задания…………………………………………………………………………. | ||
| 3. КВАНТОВАЯ ПРИРОДА ИЗЛУЧЕНИЯ……….…………………………………. | ||
| Основные формулы и законы………………………………………... | ||
| Задания…………………………………………………………………………. | ||
| 4. ЭЛЕМЕНТЫ КВАНТОВОЙ ФИЗИКИ АТОМОВ, МОЛЕКУЛ И ТВЕРДЫХ ТЕЛ……………………………………………………….. | ||
| 4.1. | Теория атома водорода по Бору..…………………………………... | |
| Основные формулы и законы………………………………………... | ||
| Задания…………………………………………………………………………. | ||
| 4.2. | Элементы квантовой механики…………………………………….... | |
| Основные формулы и законы………………………………………... | ||
| Задания…………………………………………………………………………. | ||
| 4.3. | Квантовые свойства атомов, молекул и твердых тел……... | |
| Основные формулы и законы………………………………………... | ||
| Задания…………………………………………………………………………. | ||
| 5. ЭЛЕМЕНТЫ ФИЗИКИ ЯДРА И ЭЛЕМЕНТАРНЫХ ЧАСТИЦ……………… | ||
| 5.1. | Физика атомного ядра……………………………………………………. | |
| Основные формулы и законы………………………………………... | ||
| Задания…………………………………………………………………………. | ||
| 5.2. | Физика элементарных частиц………………………………………… | |
| Задания…………………………………………………………………………. | ||
| Литература………………………..……………………………………………………….. |
Учебное издание
Егорова С.И., Ковалева В.С., Кунаков В.С.,
Лемешко Г.Ф., Наследников Ю.М., Пруцакова Н.В.
ФИЗИКА
Задания для аудиторных практических
занятий и самостоятельной работы студентов
Часть 3
Оптика, атомная физика,
физика атомного ядра
и элементарных частиц
Редактор Г.А. Бешун
Компьютерная обработка Е.В. Хейгетян
Тем план 2013 г.
В печать 01.02.2013.
Формат 60x84/16. Бумага тип №3. Офсет.
Объем 3,4 усл.печ.л. Заказ № 51. Тираж 500 экз. Цена свободная
________________________________________________________
Издательский центр ДГТУ
Адрес университета и полиграфического предприятия:
 344000, г. Ростов-на-Дону, пл. гагарина, 1.
344000, г. Ростов-на-Дону, пл. гагарина, 1.
