Волновая функция и уравнение Шредингера
4.25.Волновая функция, описывающая движение электрона в основном состоянии атома водорода, имеет вид: 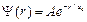 , где
, где  – нормировочный коэффициент волновой функции,
– нормировочный коэффициент волновой функции,  – расстояние электрона от ядра,
– расстояние электрона от ядра,  – первый боровский радиус. Определить наиболее вероятное расстояние электрона от ядра в основном состоянии. [
– первый боровский радиус. Определить наиболее вероятное расстояние электрона от ядра в основном состоянии. [ 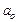 ].
].
4.26.Волновая функция, описывающая движение микрочастицы, имеет вид 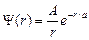 , где
, где 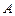 – нормировочный коэффициент волновой функции,
– нормировочный коэффициент волновой функции, 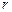 – расстояние этой частицы до силового центра,
– расстояние этой частицы до силового центра, 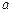 – некоторая постоянная, имеющая размерность длины. Определить среднее расстояние
– некоторая постоянная, имеющая размерность длины. Определить среднее расстояние 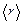 частицы от силового центра. [
частицы от силового центра. [ 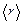 =
= 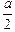 ].
].
4.27.Записать стационарное уравнение Шредингера для свободной частицы массой 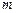 , которая движется вдоль оси
, которая движется вдоль оси 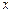 , а также определить посредством его решения собственные значения энергии. Что можно сказать об энергетическом спектре свободной частицы? [
, а также определить посредством его решения собственные значения энергии. Что можно сказать об энергетическом спектре свободной частицы? [ 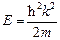 , спектр непрерывный].
, спектр непрерывный].
4.28.Электрон в бесконечно глубоком одномерном прямоугольном потенциальном ящике находится в основном состоянии. Какова вероятность обнаружения электрона в средней трети ящика? [0,609].
4.29.Волновая функция 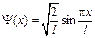 описывает основное состояние частицы в бесконечно глубоком прямоугольном потенциальном ящике шириной
описывает основное состояние частицы в бесконечно глубоком прямоугольном потенциальном ящике шириной 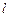 . Вычислить вероятность нахождения частицы в малом интервале ∆
. Вычислить вероятность нахождения частицы в малом интервале ∆ 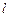 = 0,2
= 0,2 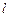 в двух случаях: 1) вблизи стенки
в двух случаях: 1) вблизи стенки 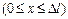 ; 2) в средней части ящика
; 2) в средней части ящика 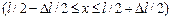 . [0,052; 0,4].
. [0,052; 0,4].
4.30.Электрон находится в бесконечно глубоком одномерном прямоугольном потенциальном ящике шириной 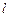 . Вычислить наименьшую разность энергий двух соседних энергетических уровней (в электронвольтах) электрона в двух случаях: 1)
. Вычислить наименьшую разность энергий двух соседних энергетических уровней (в электронвольтах) электрона в двух случаях: 1) 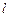 = 1 мкм; 2)
= 1 мкм; 2) 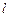 = 0,1 нм. [1,1∙10-12 эВ; 110 эВ].
= 0,1 нм. [1,1∙10-12 эВ; 110 эВ].
4.31.Вероятность обнаружить частицу на участке (a,b) одномерного потенциально-го ящика с бесконечно высокими стенками вычисляется по формуле 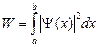 . Если . Если 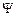 – функция имеет вид, указанный на рисунке справа, то чему равна – функция имеет вид, указанный на рисунке справа, то чему равна |  |
вероятность обнаружить частицу на участке 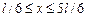 , где , где 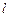 – ширина ящика. [2/3]. – ширина ящика. [2/3]. |
4.32.Пучок электронов с энергией Е = 15 эВ встречает на своем пути потенциальный барьер высотой U = 20 В и шириной 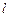 =0,1 нм. Определить коэффициент прозрачности потенциального барьера (коэффициент прохождения) D и коэффициент отражения R электронов от барьера (R + D = 1). [D = 0,1; R = 0,9].
=0,1 нм. Определить коэффициент прозрачности потенциального барьера (коэффициент прохождения) D и коэффициент отражения R электронов от барьера (R + D = 1). [D = 0,1; R = 0,9].
4.33.Частица массой 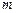 движется в одномерном потенциальном поле
движется в одномерном потенциальном поле 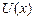 =
= 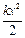 (гармонический осциллятор). Собственная волновая функция основного состояния гармонического осциллятора имеет вид
(гармонический осциллятор). Собственная волновая функция основного состояния гармонического осциллятора имеет вид 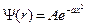 , где
, где 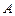 – нормировочный коэффициент;
– нормировочный коэффициент; 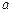 – положительная постоянная. Используя уравнение Шредингера, определить: 1) постоянную
– положительная постоянная. Используя уравнение Шредингера, определить: 1) постоянную 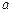 ; 2) энергию частицы в этом состоянии. [
; 2) энергию частицы в этом состоянии. [ 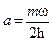 ;
; 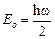 ].
].
Квантовые статистики
4.34.Показать, что при kT >> Ei (малом параметре вырождения) квантовые распределения Бозе-Эйнштейна и Ферми-Дирака переходят в классическое распределение Максвелла – Больцмана, то есть бозонный и фермионный газы приобретают свойства классического идеального газа. [ 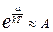 << 1;
<< 1; 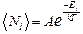 ].
].
4.35.Для каких квантовых частиц характерна знаковая неоднозначность волновой функции и какие значения спина имеют эти частицы? [фермионов; имеют полуцелые значения спина].
4.36.Для каких квантовых частиц характерна знаковая однозначность волновой функции и какие значения спина имеют эти частицы? [бозонов; имеют целочисленные значения спина].
Квантовые свойства атомов,
Молекул и твердых тел
Основные формулы и законы
· Волновые функции связанных состояний (Е < 0) атома водорода имеют вид
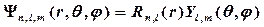 ,
,
где 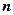 – главное квантовое число (
– главное квантовое число ( 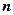 = 1, 2, 3, …);
= 1, 2, 3, …); 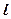 – орбитальное (азимутальное) квантовое число (
– орбитальное (азимутальное) квантовое число ( 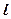 = 0, 1, 2, …, (
= 0, 1, 2, …, ( 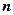 – 1));
– 1));
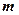 – магнитное квантовое число (
– магнитное квантовое число ( 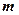 = 0, ±1, ±2, …, ±
= 0, ±1, ±2, …, ± 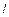 );
); 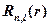 – радиальные функции, а
– радиальные функции, а 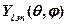 – сферические функции.
– сферические функции.
Квантовые числа 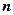 ,
, 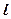 ,
, 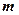 являются характеристиками микросостояния частицы, в том числе и электрона в атоме водорода, и появляются при решении нерелятивистского уравнения Шредингера.
являются характеристиками микросостояния частицы, в том числе и электрона в атоме водорода, и появляются при решении нерелятивистского уравнения Шредингера.
· Квантовое магнитное спиновое число 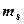 (
( 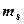 =±1/2) электрона появляется лишь при решении релятивистского уравнения Дирака, т. е. спин является релятивистской характеристикой.
=±1/2) электрона появляется лишь при решении релятивистского уравнения Дирака, т. е. спин является релятивистской характеристикой.
· Принцип Паули: в атоме два электрона не могут находиться в одном и том же квантовом состоянии (определяемом набором четырех квантовых чисел 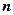 ,
, 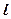 ,
, 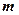 ,
, 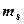 ).
).
· Электронная конфигурация атома в основном состоянии 1s2 2s2 2p6 3s2 3p6 3d10…, где числа ( 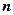 = 1, 2, 3, …) соответствуют главному квантовому числу, которое задает электронные слои (оболочки) K, L, M, N, …. Буквы латинского алфавита s, p, d, f соответствуют орбитальному квантовому числу (
= 1, 2, 3, …) соответствуют главному квантовому числу, которое задает электронные слои (оболочки) K, L, M, N, …. Буквы латинского алфавита s, p, d, f соответствуют орбитальному квантовому числу ( 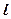 = 0, 1, 2, 3), которое задает s, p, d, f – состояния (электронные подоболочки) атома. Числа над s, p, d, f соответствуют числу электронов в соответствующих состояниях.
= 0, 1, 2, 3), которое задает s, p, d, f – состояния (электронные подоболочки) атома. Числа над s, p, d, f соответствуют числу электронов в соответствующих состояниях.
· Закон Мозли
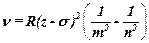 ,
,
где 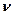 – характеристические частоты спектра;
– характеристические частоты спектра; 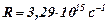 – постоянная Ридберга;
– постоянная Ридберга; 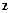 – заряд ядра атома в относительных единицах;
– заряд ядра атома в относительных единицах; 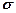 – постоянная экранирования;
– постоянная экранирования; 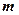 и
и 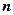 – квантовые числа, соответствующие энергетическим уровням, между которыми совершается переход электрона в атоме.
– квантовые числа, соответствующие энергетическим уровням, между которыми совершается переход электрона в атоме.
· При 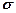 = 0 формула закона Мозли обращается в формулу, описывающую линейчатые спектры водородоподобных атомов
= 0 формула закона Мозли обращается в формулу, описывающую линейчатые спектры водородоподобных атомов
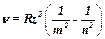 .
.
При 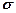 = 0 и
= 0 и 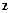 = 1 формула закона Мозли совпадает с обобщенной формулой Бальмера для линейчатого спектра атома водорода.
= 1 формула закона Мозли совпадает с обобщенной формулой Бальмера для линейчатого спектра атома водорода.
· Частоты излученного или поглощенного электромагнитного кванта молекулярного спектра
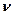 =
= 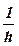 (∆ Wэл. + ∆ Wкол. + ∆ Wвр.),
(∆ Wэл. + ∆ Wкол. + ∆ Wвр.),
где ∆Wэл., ∆Wкол. и ∆Wвр. – разности энергий двух соответственно электронных, колебательных и вращательных уровней.
· Средняя энергия квантового одномерного осциллятора
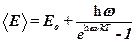 ,
,
где 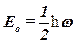 – нулевая энергия;
– нулевая энергия; 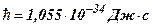 - постоянная Планка;
- постоянная Планка; 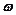 – циклическая частота колебаний осциллятора;
– циклическая частота колебаний осциллятора; 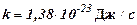 – постоянная Больцмана;
– постоянная Больцмана;
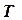 – термодинамическая температура.
– термодинамическая температура.
· Молярная внутренняя энергия системы, состоящей из невзаимодействующих квантовых осцилляторов
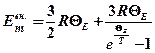 ,
,
где 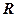 – молярная газовая постоянная;
– молярная газовая постоянная; 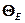 =
= 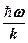 – характеристическая температура Эйнштейна.
– характеристическая температура Эйнштейна.
· Молярная теплоемкость кристаллического твердого тела в области низких температур (предельный закон Дебая)
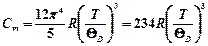 ( T <<
( T << 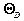 ),
),
где 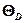 =
= 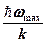 – характеристическая температура Дебая.
– характеристическая температура Дебая.
· Распределение свободных электронов в металле по энергиям при 0 К
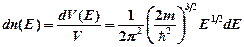 ,
,
где 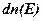 – концентрация электронов, энергия которых заключена в пределах от
– концентрация электронов, энергия которых заключена в пределах от 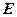 до
до 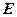 +
+ 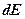 ;
; 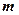 – масса электрона. Это выражение справедливо при
– масса электрона. Это выражение справедливо при 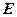 <
< 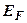 (
( 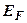 – энергия или уровень Ферми).
– энергия или уровень Ферми).
· Энергия Ферми в металле при Т = 0 К
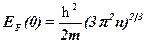 ,
,
где 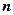 – концентрация электронов в металле.
– концентрация электронов в металле.
· Средняя энергия электронов
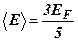 .
.
· Удельная проводимость собственных полупроводников
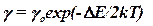 ,
,
где 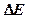 – ширина запрещенной зоны;
– ширина запрещенной зоны; 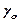 - константа.
- константа.
· Сила тока в p-n – переходе
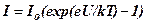 ,
,
где 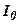 – предельное значение силы обратного тока;
– предельное значение силы обратного тока;
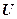 – внешнее напряжение, приложенное к p-n – переходу.
– внешнее напряжение, приложенное к p-n – переходу.
· Связь между глубиной 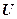 потенциальной ямы и работой выхода
потенциальной ямы и работой выхода 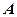 из металла и полупроводника:
из металла и полупроводника:
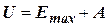 ,
,
где 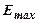 – максимальная энергия электрона в яме.
– максимальная энергия электрона в яме.
· Внутренняя контактная разность потенциалов
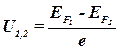 ,
,
где 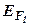 и
и 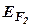 - энергия Ферми соответственно для первого и второго металла или полупроводника;
- энергия Ферми соответственно для первого и второго металла или полупроводника; 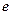 – заряд электрона.
– заряд электрона.
Задания
Квантовая физика атома
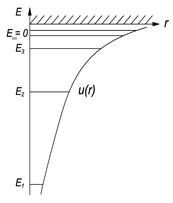 |
4.37.Уравнение Шредингера для стационарных состояний электрона, находящегося в атоме водорода, задается в декартовых координатах уравнением 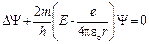 .
.
Представить 1) собственные значения энергии, удовлетворяющие уравнению; 2) график потенциальной энергии взаимодействия электрона с ядром; 3) возможные дискретные значения энергии на этом графике. [1) 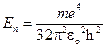 ,
,  =1, 2, 3,…
=1, 2, 3,…
2), 3) см. рисунок справа].
4.38.От каких квантовых чисел зависят соответственно радиальная 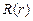 и сферическая
и сферическая 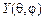 функции, входящие в волновую функцию связанных состояний атома водорода? [
функции, входящие в волновую функцию связанных состояний атома водорода? [ 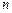 ,
, 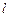 ;
;  ,
,  ].
].
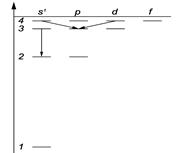 | 4.39.На рисунке слева схематически представлена система энергетических уровней атома водорода. Какие переходы запрещены правилами отбора? [3s→2s]. |
4.40.Пользуясь условными обозначениями состояний электрона в атоме водорода, записать переходы, приводящие к возникновению серии Бальмера.[ns→2p; nd→2p] (n = 3, 4, …).
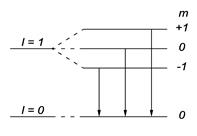 |
4.41.Объяснить диаграмму, иллюстрирующую расщепление энергетических уровней и спектральных линий (с учетом правил отбора) при переходах между состояниями с 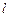 = 1 и
= 1 и 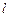 = 2. [p – состояние:
= 2. [p – состояние: 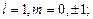 s – состояние:
s – состояние: 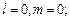
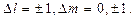 ].
].
4.42.Нормированная волновая функция, описывающая
1s – состояние электрона в атоме водорода, имеет вид 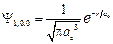 , где
, где 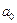 – первый боровский радиус. Определить среднюю потенциальную энергию электрона в поле ядра. [
– первый боровский радиус. Определить среднюю потенциальную энергию электрона в поле ядра. [ 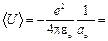 – 27,2 эВ].
– 27,2 эВ].
4.43.Определить, во сколько раз орбитальный момент импульса электрона, находящегося в d – состоянии, больше, чем для электрона в p – состоянии. [1,73].
4.44.Записать электронную конфигурацию атома фосфора с вакансией в 2p – подоболочке. [1s2 2s2 2p5 3s2 3p3].
4.45.Записать квантовые числа, определяющие внешний, или валентный, электрон в основном состоянии атома алюминия. [ 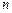 = 3,
= 3, 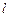 = 1,
= 1, 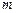 = 0, ±1;
= 0, ±1; 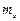 = ±1/2].
= ±1/2].
Закон Мозли
4.46.Определить наименьшую длину волны рентгеновского излучения, если рентгеновская трубка работает при напряжении U = 30 кВ. [41,3 пм].
4.47.Считая, что формула закона Мозли с достаточной степенью точности дает связь между характеристическими частотами рентгеновского спектра и порядковым номером элемента, из которого сделан антикатод, найти наибольшую длину волны К-серии рентгеновских лучей, даваемых трубкой с антикатодом из: 1) железа, 2) меди, 3) молибдена, 4) серебра, 5) тантала, 6) вольфрама, 7) платины. Для К – серии постоянная экранирования 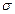 = 1. [1) 194 пм; 2) 154 пм; 3) 71,2 пм; 4) 56,3 пм; 5) 22 пм; 6) 21,4 пм; 7) 19 нм].
= 1. [1) 194 пм; 2) 154 пм; 3) 71,2 пм; 4) 56,3 пм; 5) 22 пм; 6) 21,4 пм; 7) 19 нм].
4.48.Определить постоянную экранирования для L – серии рентгеновских лучей, если известно, что при переходе электрона в атоме вольфрама с М- на L-слой испускаются рентгеновские лучи с длиной волны 143 пм. [ 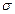 = 5,5].
= 5,5].
4.49.Определить элемент и его порядковый номер в периодической системе элементов Д.И. Менделеева, если граничная (наибольшая) частота К – серии характеристического рентгеновского излучения составляет 5,55∙1018 Гц. [z = 42, молибден].
4.50.При переходе электрона в атоме с L- на К-оболочку испускаются рентгеновские лучи с длиной волны 78,8 пм. Какой это атом? Для К-серии постоянная экранирования 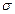 = 1. [z = 40, цирконий].
= 1. [z = 40, цирконий].
4.51.В излучении звезды обнаружен водородоподобный спектр, длина волны которого в 4 раза меньше, чем у атомарного водорода. Определить элемент, которому принадлежит данный спектр. [z = 2, гелий].
4.52.Молекулярные спектры состоят из трех видов полос:
1) вращательных; 2) колебательно-вращательных и 3) электронно-колебательных, которые в свою очередь состоят из большого числа тесно расположенных линий. В эксперименте и в теории проявляется значительное различие в разности энергий двух соответственно электронных, колебательных и вращательных уровней, между которыми разрешены переходы электрона в соответствии с правилами отбора, причем ∆Wэл.>∆Wкол.>∆Wвр. Определить, какие полосы будут наблюдаться соответственно на: 1) длинноволновой и 2) коротковолновой границах молекулярного спектра при возбуждении всех приведенных выше полос полосатого спектра молекулы. [1) вращательные; 2) электронно-колебательные].
